태양의 지위를 이용한 진북 추출 장치의 구현
Copyright © The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
천측력을 이용하여 태양 또는 별의 위치를 구하고, 이를 항해에 이용하는 천문항해는 오랜 기간 항해사들의 기본적이고도 중요한 업무로 인식되었다. 선박이 항해를 하기 위해서는 위치를 결정하고 진북을 기준으로 나아가야 할 방위를 정하는 과정이 있어야 한다. 20세기 중반까지 항해사들은 선박의 위치를 알기 위해 천측력과 태양, 별 등을 관측하고 복잡한 계산을 수행하였으며, 방위를 추출하기 위해서는 마그네틱 컴파스나 자이로 컴파스를 이용하였다. 이후 등장한 LORAN(LOng RAnge Navigation)이나 GPS(Global Positioning System) 등의 전파항법을 통해 선박의 위치를 쉽게 구할 수 있게 되었으며, 그 정확도도 매우 높다. 하지만 선박의 방위를 알기 위해서는 여전히 컴파스를 사용하고 있는데, 마그네틱 컴파스는 지자기장과 자성물체의 영향으로 오차가 발생하고 자이로 컴파스는 안정적인 전원 공급 및 지속적인 작동을 필요로 한다. 따라서 본 논문에서는 천문항법을 이용하여 태양을 관측함으로써 진북을 편리하게 추출하여 방위를 제공하는 방법을 제시하고자 한다. 특히 최신의 IT 임베디드 기술과 접목하여 측정과 동시에 약 0.2˚ 이하의 오차로 구현할 수 있게 되었다.
Abstract
Astronomical navigation has long been recognized as a basic and important task for navigators. It uses the Nautical Almanac to determine the position of a ship from the positions of the sun or stars. During a voyage, it is important to determine the position and bearing of the ship that is based on the true north. Until the middle of the 20th century, navigators observed the sun or stars and performed complicated calculations using the Nautical Almanac to know the positions of ships. They also calculated the bearings using magnetic or gyro compasses. Since then, the position of a ship can be easily calculated through radio navigation such as LORAN (LOng RAnge Navigation) or GPS (Global Positioning System) with very high accuracy. Although compasses are still used to measure the bearing of a ship, magnetic compass readings are susceptible to error due to the influence of the geomagnetic field and/or magnetic objects, while the gyro compass requires a stable power supply and continuous operation. Here we propose a simple method to conveniently calculate the true north by observing the sun, using astronomical navigation. Using the latest IT embedded technology, this method can be implemented with an error of less than about 0.2 °.
Keywords:
Celestial navigation, Compass, Azimuth, Error correction, True north키워드:
천문항해, 컴파스, 방위, 오차수정, 진북1. 서 론
태양이나 별의 지위를 산출하여 천문항해를 하는 것은 항해사들의 기본적인 업무로써, 이를 통해 선박의 위치를 산출하고 방위를 구하여 항해를 하였다.
오늘날 위치를 알려주는 GPS와 정확한 방위를 제공하는 자이로 컴파스가 널리 사용되는 것과는 달리, 과거에 항해사들은 위치를 산출하고 방위를 찾는데 많은 시간과 노력을 기울였다. 특히 선박 운항에 필요한 방위를 얻기 위해서는 천체 관측을 통해 위치를 산출한 이후에, 다시금 복잡한 계산을 수행하였다. 개략적인 방위는 마그네틱 컴파스를 통하여 얻을 수 있었으나 지자기장이나 다른 철 구조물 등의 영향으로 인하여 많은 오차를 가지는 단점이 있었다[1].
자이로 컴파스의 등장으로 인하여 지구자기장의 영향 없이 정확한 방위 제공이 가능하였으나, 이를 구비하기 위해서는 고가의 자이로 컴파스를 탑재하고 장비 작동을 위해서는 안정적인 전원 공급이 필요하다. 중대형 선박 위주로 자이로 컴파스가 탑재되고 있으며, 소형 선박들은 마그네틱 컴파스를 주로 이용하고 GPS에서 제공되는 기능을 통해 방위를 확인하고 있다.
따라서 본 논문에서는 예로부터 선박의 항해를 위해 사용되어 온 천문항법의 복잡한 계산과정을 현대의 IT 기술에 접목하는 방안을 제시하고자 한다. 이러한 최신의 IT 기술을 이용한 진북 추출은 주간 중에 선박의 항해를 위한 방위 제공 또는 컴파스의 오류를 수정할 수 있을 뿐만 아니라, 육상의 특정 지점에서 정확한 방위를 간단하게 구할 수 있어 그 활용성은 매우 높다고 할 것이다.
본 논문은 모두 5장으로 구성하였다. 서론에 이어 2장에서는 이론적인 근거를 제시하기 위해 천문항법의 이론적 개념을 설명하였고, 3장에서는 진북 추출 알고리즘 및 장치 구현을 위한 과정을 설명하였으며, 4장에서는 시험 환경을 구축하고, 시험 및 평가를 통해 결과 값을 산출한 후 정확성을 확인하였고, 5장에서는 연구의 결과를 정리하였다.
2. 천문항해의 주요 개념
2.1 천체의 지위
유클리드 공간에서 두 지점간의 방위를 구하기 위해서는 평면위의 두 지점 좌표가 반드시 필요하다. 즉, 2차원적인 평면에서는 P1:(x1, y1), P2:(x2, y2)의 좌표에 의해 P1에서 P2를 바라보는 각을 구할 수 있다. 이때 북쪽을 기준으로 혹은 다른 임의의 지점을 기준으로 한 P1과 P2의 각도를 구하는 것은 어려운 일이 아니다.
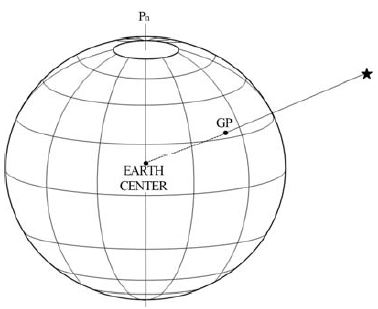
천체를 지구상의 P2 지점으로 구체화하기 위해서는 지위의 개념이 필요하다. 천체와 지구중심을 연결한 직선이 지구표면과 만나는 점을 지위(Geographical Position : GP)라고 부른다. Figure 1과 같이 천정 바로 아래가 관측자의 위치인 것처럼 천체 바로 아래가 지위이다[2]. 지위는 적위(Declination ; Dec.)와 본초시각(Greenwich hour angle ; GHA)과 관련되어 있으며, 위도와 경도에 대응한다. 적위는 적도를 기준으로 남과 북의 접미부호를 가지고 경도는 동서의 접미부호를 가지는 반면, 본초시각은 동서의 구분 없이 0°에서 360°까지의 값을 가진다.
Geographical Position
천체를 지나는 천의 자오선 상에서 천의 적도로부터 천체까지의 호를 그 천체의 적위라 하며 지구상의 위도에 대응하는 것이다. 적도 상의 0°에서 남북으로 각각 90°까지 측정하고, 천체가 적도의 북쪽에 있으면 부호 N을, 남쪽에 있으면 부호 S를 붙인다[3].
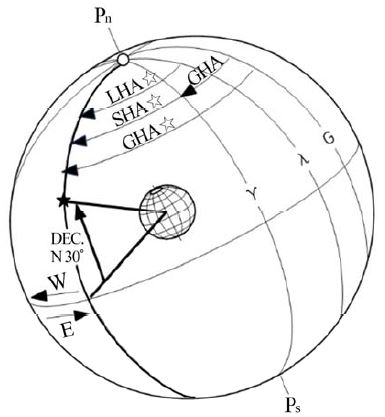
Figure 2에 적위와 시각의 개념을 함께 도시하였다. 지방시각(Local Hour Angle ; LHA)은 관측자의 천의 자오선으로부터 천체의 시권까지 시각을 말하고, 항성시각(Sidereal Hour Angle ; SHA)은 춘분점(ϒ)의 시권으로부터 천체의 시권까지의 시각을 말한다.
Declination and Hour Angle
이상을 토대로, 위도와 경도를 이용하여, 관측자 위치 P1과 지구 위에 천체의 좌표인 지위 P2를 표현하기 위해 지구상 좌표는 GHA와 Dec.로 표시하였다. 여기서 천체는 태양을 이용하였다.
2.2 천문항해를 이용한 진북
선박이 항해하는데 필요한 방위를 구하기 위해서는 선박의 위치에서 진북을 우선적으로 추출하여야 한다. 진북을 기준으로 선박의 Heading(선수방향)이 가리키는 방위가 바로 그 선박이 진행하는 방위이다.
컴파스는 진북 또는 자북을 일정하게 가리키도록 고안되어 있으며, 그에 따른 신호를 선박의 각 요소에 제공함으로써 현재 선박이 진행하는 방위를 알 수 있게 된다. 마그네틱 컴파스는 자석을 이용해 자침이 지구 자기의 방향을 지시하도록 만든 장치로써, 오차에는 편차와 자차가 있다. 편차는 진북과 자북의 교각으로 지자기로 인하여 발생하고, 자차는 마그네틱 컴파스의 북과 자북과의 교각으로 선체자기로 인하여 발생한다[4].
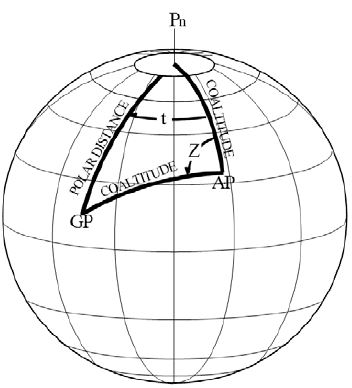
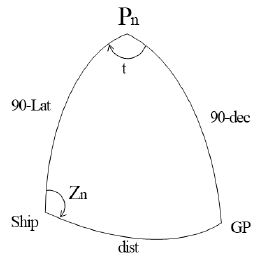
천문항법을 이용하여 진북을 추출하기 위해서는 항해삼각형에 대한 이해가 필요하다. 관측자의 좌표와 천체의 좌표 사이의 각도를 계산하는데 있어 항해삼각형을 이용할 수 있다. Figure 3은 항해삼각형을 도식화 한 것이다. 항해삼각형의 세 변은 여위도(Colatitude), 극거리(Polar distance) 및 여고도(Coaltitude)라 하고 세 각은 자오선각(Meridian angle), 방위각(Azimuth angle) 및 위치각(Parallactic angle)이다. 항해삼각형의 계산은 구면삼각법의 해법에 의한 것으로, 삼각함수를 이용하게 된다.
Navigational Triangle
태양의 방위를 구하기 위해 천측력을 이용할 경우, 우리나라에서는 국립해양조사원에서 발행하는 천측력을 이용하여 1시간 간격으로 표시되어 있는 지위를 구할 수 있다. 태양은 1시간에 15º 의 GHA 변경이 발생하므로 정확한 값의 계산에 신중을 기하여야 한다[5]. Sight Reduction(천측계산표)를 이용하여 선박에서 측정한 태양의 진북 대비 방위를 산출할 수도 있다. 그러나 이 표는 선박의 위치를 도 단위로만 산출할 수 있으므로 선박의 정확한 위치를 기준으로 정확한 방위를 산출하기 위해서는 별도의 계산이 요망된다[6].
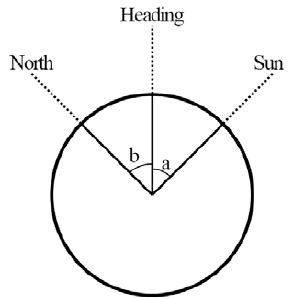
Figure 4는 관측자의 실제 진북을 기준으로 b 각도만큼의 Heading으로 선박이 운항하고 있을 때, Heading을 기준으로 a 각도만큼 태양이 관측 되었을 때를 가정하여 도식화한 그림이다.
Observation Example
Figure 4에서 보듯이 특정 시간 및 위치에서 천측계산표를 이용하여 구해진 태양의 진북 대비 방위는 각 a + b를 의미한다. 구해진 태양의 방위값을 역으로 적용한다면 태양을 보는 방위에서 진북을 찾아낼 수 있게 된다. 즉, 태양의 방위에서 -(a+b)는 진북(True North)를 가리키게 된다.
3. 진북 추출 알고리즘
3.1 방위 추출 알고리즘의 구현
천체를 관측하여 진방위를 구하는 천체의 방위각법에는 시진방위각법, 출몰방위각법, 고도방위각법 등이 있다.
Napier’s analogie에 의한 시진방위각법을 이용하여 방위를 추출하는 방법은 수식이 매우 복잡하며 각종 방위각표를 사용해야 하는 어려움이 있다. 본 논문에서는 항해삼각형을 전산화가 가능한 식으로 해석하여 방위를 추출할 수 있는 알고리즘을 제시한다[7]. 항해삼각형을 이용한 수식은 삼각함수의 사인법칙과 코사인법칙을 활용하였다. 방위각표 등을 이용하여 수동을 계산하는 기존의 시진방위각법에 비하여 항해삼각형을 전산화함으로써 신속성과 편리성은 물론 높은 정확도도 갖게 되었다.
Figure 5에서 각 Zn 방위를 구하기 위해서는 경도(Long) 성분의 세밀한 고려가 필요하다. 자오선각(Meridian Angle ; t) 대비, 경도는 시각성분이므로 지방시각인 LHA에 대하여 경도가 E이면 +, W이면 –로 하여 t = GHA ± 경도가 된다. 단, LHA가 360도를 넘으면 t = LHA-360로 계산 하여야 한다. t는, LHA < 180° 이면 t = LHA(W)가 되고, LHA > 180° 이면 t = 360 – LHA(E)로 구할 수 있다.
Sunrise at the Ship's Position
방위 Zn을 구하기 위해 요구되는 선박과 태양의 지위간의 거리를 dist라 하고 이를 구하기 위해, 식 (1)과 같이 계산한다
| (1) |
이렇게 구해진 dist를 이용하여 선박에서 바라보는 태양의 방위를 구하면, 식 (2)와 같이 계산할 수 있다.
| (2) |
여기서 주의할 점은, 식 (1)에서 t는 cosine에 대한 인수이다. cosine 의 특성상 –90°에서 90°까지의 값은 양의 값으로 표현되므로 선박의 위치와 지위의 위치간격 dist는 단지 거리만 표시할 뿐, 두 지점간의 전후 비교가 불가하다. 즉, 선박에서 오전에 태양을 관측한 것인지, 오후에 태양을 관측한 것인지 알 수 없고, 두 지점에 대한 스칼라 값이 된다는 것을 알 수 있다.
또한 식 (2)에서 방위 Zn 역시 cosine의 인수이므로 180° 이상의 값을 표현하지 못한다. 즉, 선박을 기준으로 태양이 저물고 있는 오후를 나타낼 경우, 태양은 이미 관측자의 자오선을 앞질러 있고, Zn은 180° 이상의 값으로 표현되어야 한다.
따라서 식 (2)에서 Zn은 t가 270° 보다 클 때, 즉 태양이 관측자를 지나 친 오후에 한하여 식 (3)과 같이 표현하여야 한다.
| (3) |
3.2 태양의 지위 추출
과거부터 지금까지 태양의 지위를 구하는 방법은 천측력을 이용하는 것이었다. 천측력은 1시간 단위로 GHA와 Dec.가 기록되어 있는데, 항해사는 원하는 시간에 천체의 지위를 알기 위해 천측력에서 해당 시각의 앞 뒤 시각의 지위들을 찾아 현 시각에 대한 보정 과정을 통해 정확히 구할 수 있다. 상기에서 설명하였듯이 선박의 위치 P1에 대한 태양의 P2의 좌표가 정확할수록 방위의 정밀한 계산이 가능하다.
태양은 북회귀선과 남회귀선 사이를 1년을 기준으로 이동한다. 따라서 23.5°에서 –23.5° 총 47°의 변화량을 가지며, 1년에 2회 변화하므로 Dec.의 시간 당 변화량을 계산할 수 있다. 계산하면 47° / (365/2)일 / 24시간 = 38.6″이 되므로 평균 38.6" 정도가 된다. 이는 시간당 1분 미만의 변화량으로 계산에 큰 영향을 미치지 않는다. 이에 비해 지구의 자전주기는 1일이므로, 시간 성분인 태양의 GHA는, 360°/24시간으로 계산한다면 시간당 약 15°의 변화량을 보인다. 태양관측을 통한 방위를 추출하는데 있어서, 태양의 Dec. 성분의 변화보다는 GHA 성분의 변화가 방위의 측정에 미치는 영향이 매우 크다는 것을 의미한다. GHA는 시간에 대한 Factor 이므로 시각의 정밀성도 함께 요구됨을 알 수 있다.
선박의 운항 중에 태양을 관측한 후 천측력을 찾아 태양의 지위를 파악하고, 계산과정을 거쳐 선박의 위치를 기반으로 방위를 산출하기 까지는 많은 시간 소요가 불가피하다. 편리한 전자계산기를 사용하더라도, 선박에서 일련의 계산과정을 진행하는데 있어 시간 지연 및 오차는 필연적으로 발생할 수밖에 없다. 태양관측의 정확성에 영향을 미치는 오차 중에서 Dec. 성분은 1시간의 시간 차이에 대헤서 1-4분 이내의 오차값을 가지나, GHA의 경우 1시간의 시간 차이는 15º에서 많게는 90º 이상의 오차를 발생시키게 되어 매우 치명적이라 할 수 있다.
태양관측 과정에서의 오차에는 첫째, 선박에 장착된 크로노미터 혹은 선박 시계의 GMT 와의 오차, 둘째, 실제 관측시간과 기록된 관측시간 사이의 오차, 셋째, 관측 장비 사용상의 운용자 오차, 넷째, 관측장비의 기계적 오차, 다섯째, 계산상의 오류 등이 있으며, 각각의 오차가 수작업을 통한 계산 과정에서 영향을 미치게 된다. 따라서 태양관측을 통한 정확한 방위의 추출을 위해서는 정확한 GMT 시각의 제공과 정확한 관측장비의 작동, 그리고 무엇보다 시간적인 지체없이 방위를 추출하는 계산기가 함께 존재해야 하는 것이다. 따라서 본 논문에서는 이러한 문제 해결을 위해 임베디드화한 태양관측 장비를 구현하여 이를 측정하였다.
본 논문에서는 시간적인 오차를 최소화하기 위해 태양 관측 시 버튼을 눌러 그 시점에서의 지위를 바로 산출하고, 1초 이내로 방위를 산출하도록 시스템을 구성하였다. 또한 이러한 시간 보정에 따른 오차 발생의 최소화를 위해, 본 논문에서는 IAU(International Astronomy Union : 국제 천문 협회)에서 제공하는 태양의 운동에 관한 방정식을 이용하였다[8].
3.3 방위 추출장치의 구현
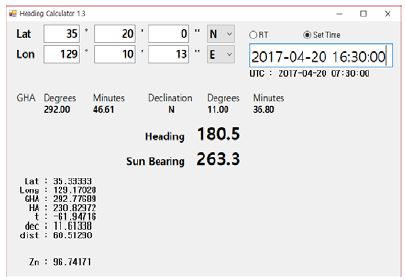
Figure 6의 GUI는 제안한 알고리즘을 토대로 구성한 S/W를 표시한 것이다. 위도와 경도를 자동 혹은 수동으로 입력 가능하도록 구성하였으며, 특히 시각의 경우 UTC 표준시를 사용할 수 있도록 초단위로 표시하였다. 선박의 Heading과 관측한 태양의 진북 대비 방위를 계산하였으며, GHA와 Dec. 등의 세부적인 연산 값들이 표시될 수 있도록 하였다. 특히 태양의 지위는 국제표준에 따른 계산식을 도입하여 이를 국립해양조사원 발행의 천측력과 비교 분석하여 동일함을 확인하였다.
Calculating Software
Figure 6의 S/W는 C# .NET Framework 2.0 환경에서 개발하였고, 임베디드 하드웨어와의 인터페이스는 USB to RS422 컨버터를 통해 통신하였다. 임베디드 시스템은 RS422 통신의 NMEA 신호 출력이 가능하도록 구성하였다.
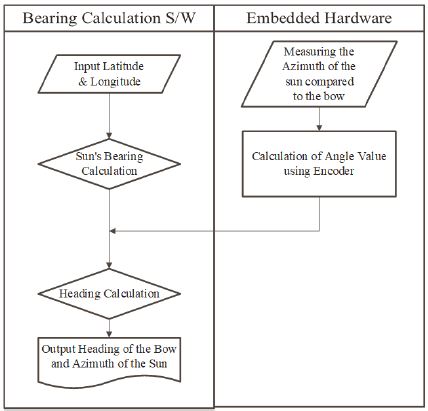
Figure 7은 개발한 임베디드 시스템의 동작 블록도를 도식화한 것이다.
Block Diagram of Embedded Systems
Figure 8은 임베디드 시스템의 하드웨어 모습이며, 이는 기존의 과거 아날로그 방위환과 엔코더 시스템이 접목된 형태인데, 효율적인 소숫점 연산을 위해 Cortex-M4 코어 기반의 STM32F407 마이크로프로세서를 사용하여 168MHz의 클록 속도를 가지도록 하였다.
Implementation of Embedded Systems
이러한 임베디드 시스템은 해당 시각의 위도 및 경도를 자동 혹은 수동으로 입력받아 앞서 제시한 알고리즘을 통해 태양의 방위를 계산한다. 임베디드 시스템의 방위환을 통해 선수 대비 태양의 방위각을 엔코더를 통해 구하고 이를 태양방위 값과 비교 연산하여 선박의 Heading 방위를 출력한다.
4. 시험 및 평가
앞서 제시한 알고리즘에 따라 구현된 임베디드 시스템을 시험하는데 있어 실제 선박을 이용하기 어려운 점을 고려하여 유사한 시험환경을 별도로 구성하였다. 본 논문에서는 한 지점에서 일정한 시간 간격으로 태양을 반복 측정함으로써 진북을 추출하고, 얻어진 진북을 기준으로 선박의 Heading 값을 구하는 방법을 시행하였다.
시간이 변함에 따라서 태양의 지위가 변하게 되고, 관측되는 태양의 방위도 달라지는 시험환경에서 선박의 Heading이 일정한 값을 유지하고, 그 오차 범위가 허용할 수 있는 수준이라면 우리가 구하고자 하는 진북 추출 과정이 제대로 되고 있다는 것을 의미하는 것이다.
따라서 본 논문에서는 선박의 Heading을 계속 구하여 이 값이 얼마나 일정하게 얻어지는지를 시험하였다.
Table 1은 임베디드 시스템을 이용하여 얻어진 4회의 시험결과를 나타낸 것이다. 1차 테스트 및 3차 테스트는 부산광역시 영도구 태종로 727 (35.074913N, 129.086150E)에서 Heading의 정확도를 검증하였다. 1차의 경우, 2시간 동안 20분 간격으로 총 7회 측정을 진행하였고, 3차의 경우 1시간 30분 동안 10~30분 간격으로 총 8회 측정하였다. 2차 테스트 및 4차 테스트는 부산광역시 영도구 남항서로 52(35.085579N, 129.034898E)에서 Heading의 정확도를 검증한 것으로, 2차의 경우 30분 간격으로 총 8회를 측정하였으며, 4차의 경우 10분 간격으로 1시간 10분 동안 총 8회를 측정한 것이다.
Astronomical Observation & Heading
네 번의 테스트 결과 측정치는 평균 오차가 0.21°, 0.20°, 0.19°, 0.19° 로 나타났으며 이를 합산한 총 오차는 0.193°로 계산 되었다. 이것은 각각의 시험 결과가 매우 유사한 오차 분포를 보이며 일정 범위 내의 오차를 나타낸 것임은 물론, 전체적인 오차는 0.2°이하의 양호한 결과가 나타난 것이라 사료된다.
IMO Resolution MSC 116(73)은 선박에 탑재되는 THD(Transmitting Heading Device)에 대하여 규정하고 있는데, THD의 Static Error는 그 허용범위를 1° 이하로 규정하고 있다[9]. TG-8000/8500은 Tokyo KEIKI에서 생산되는 Gyro 컴파스로 IMO 규정에 명시된 허용오차를 충족하는 제품으로 선박에 장착되는 제품이다. 또한 JLR-21은 일본 JRC의 GPS 컴파스로 이미 많은 선박에서 운용되고 있는 제품이다[10][11].
Table 2에서 보는 바와 같이 본 실험에서 제시한 방위 오차는 국제적으로 통용되는 기준을 충족하고 있으며, 선박 운항을 위한 방위의 추출 장비로서 사용 가능함을 알 수 있다. 특히 본 연구를 통해 구현된 Table 1의 결과는 Table 2에서 제시한 대부분의 장비들의 오차 범위 내에서 방위의 검출이 가능하므로, 이들 장비의 오차 보정용 혹은 방위 산출을 위해 사용 가능함을 확인할 수 있었다.
Heading Error Tolerance
따라서 상기 시험 내용을 토대로 본 연구의 진북 산출 시험 결과는 IMO의 컴파스 기준은 물론 현재 시판되고 있는 방위 관련 제품들의 방위 정확도의 허용 오차를 만족함을 알 수 있었다. 또한 방위환을 이용하여 태양을 관측한 값이 임베디드 시스템을 통해 자동으로 선박의 Heading을 산출하게 된다. 이러한 편의상 장점은 본 연구에서는 정량화하지 못하였지만 실무에서는 많은 공감을 얻을 것으로 사료된다.
5. 결 론
본 논문에서는 천문항법을 통해 선박에서 진북을 구하던 과정을 IT 임베디드 기술과 접목하여 자동화하는 방법에 대하여 제안하였다. 이를 위해 과거의 태양관측 및 계산 기법을 현대의 IT 기술로 접목이 가능하도록 알고리즘을 정리하였고, 이러한 알고리즘을 S/W로 구현하여 이를 임베디드 시스템 속에 접목하였다.
본 논문에서 구현된 임베디드 시스템은 관측되어진 태양 방위값과 시간을 이용하여 관측 위치에서의 진북을 계산하고 현재 선박의 Heading이 얼마인지를 나타내는 일련의 계산과정을 자동으로 수행할 수 있는 SW를 탑재하고 있다.
4차의 테스트 결과 평균 0.2° 이하의 오차를 보이는 시험결과를 얻었다. 이는 IMO 기준의 방위의 허용오차 범위를 만족하는 것이며, 항해를 위해 사용되는 대부분의 컴파스의 정확성과 비교하여도 좋은 결과임을 알 수 있었다. 이러한 정확도를 고려할 때, 선박에 탑재된 자이로 컴파스나 마그네틱 컴파스의 정확성 검증이나 오차를 보정할 때에도 제한적으로 사용할 수 있을 것이다. 또한 GPS 장비에만 의존하는 소형선박의 경우 고가의 자이로 컴파스를 설치하지 않더라도 주간 중에 한 두 번의 태양관측만으로 항해에 어느 정도 도움을 제공하는데 충분하다고 할 것이다.
기존의 천문항법에서는 태양을 관측하고 천측력, 천측계산표, 각종 방위각표 등을 이용하고 일련의 복잡한 계산과정을 거쳐야만 하였다. 하지만 본 임베디드 시스템에서 구현된 SW 기술을 이용한다면 주간 중 태양관측만으로 방위 산출이 가능하므로 기존 대비 시간 단축과 편의성 증대도 기여할 수 있을 것이다. 따라서 본 논문의 결과를 활용한다면 방위의 정확성을 필요로 하는 각종 장비의 개발 등에도 도움이 될 수 있을 것이라 사료된다.
References
- S. G. Lee, The Theory of New Navigation’s Equipments, Busan, Korea, Dasom Publishing, (2002), (in Korean).
- S. G. Park, Celestial Navigation, Seoul, Korea, Yeonkyeong Publishing, (2007), (in Korean).
- Y. J. Yoon, Celestial Navigation, Busan, Korea, Korea Maritime University Press, (1999), (in Korean).
- T. J. Cutler, Dutton’s Nautical Navigation, MD, USA, U.S.Naval Institute Press, (2004).
- Korea Hydrographic and Oceanographic Agency, “2016 natical almanac”, (2017), (in Korean).
- Korea Hydrographic and Oceanographic Agency, “Sight reduction tables for marine navigation”, vol 3, (2017), (in Korean).
- J. Karl, Celestial Navigation in the GPS Age, CA, USA, PARADISE CAY Publications, (2011).
- J. Meeus, Astronomical Algorithms, VA, USA, Willmann-Bell Inc., (1991).
- Performance Standards for Marine Transmitting Heading Devices (THD), IMO Resolution MSC 116(73), http://www.imo.org/en/KnowledgeCentre/IndexofIMOResolutions/Maritime-Safety-Committee-(MSC)/Documents/MSC.116(73).pdf Accessed October 10, 2017.
- Tokyo Keiki Gyrocompass TG-8000/8500 Datasheet, http://www.tokyo-keiki.co.jp/marine/e/products/pdf/TG-8000_e_201512.pdf Accessed October 10, 2017.
- Japan Radio 3D Dynamic sensor GPS COMPASS / GPS NAVIGATER: JLR-31/JLR-21 Brochure, http://www.jrc.co.jp/eng/product/lineup/jlr21_31/pdf/JLR-31.pdf Accessed October 10, 2017.