분사액적 분포특성 향상을 위한 충돌면의 분석

2.1 계산 조건

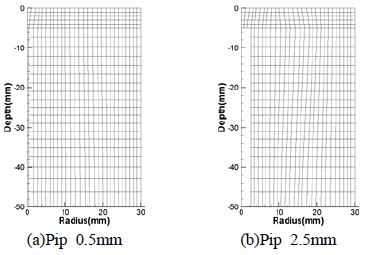
직접 가압방식인 PJ fine atomizing 타입 노즐[6]을 대상으로 하였으며, 충돌면의 반경과 노즐에서 충돌면까지의 거리를 조절하여 액적의 분무거동을 분석하였다. Figure 1은 축대칭 원통의 중심에서 반경방향으로의 계산격자를 나타내며, Figure 1 (a)는 노즐과 충돌면의 사이 거리가 3mm이고 충돌면의 반경이 0.5mm인 경우이고, Figure 1 (b)는 노즐과 충돌면의 사이 거리가 7mm이고 충돌면의 반경이 2.5mm인 경우이다.

Figure 1:

Calculation grids

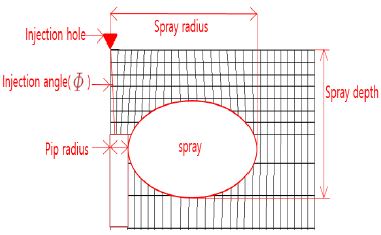
Figure 2는 본 논문에서 사용되는 충돌분무에 대한 용어로서 분무반경, 분무깊이 등을 나타낸다.

Figure 2:

Definitions

Table 1은 계산조건 전체를 나타내며, 충돌반경이 0.1에서 2.5까지이며 노즐에서 충돌면까지의 거리가 3 ~ 7mm로 총 45가지의 계산조건을 나타낸다.

Table 1:

Calculation condition

연구대상의 노즐과 분위기 조건은 Table 2와 같다. 대상노즐의 분공경과 압력 및 분사각은 각각 1 mm, 1.5 bar, 2°이며, 분위기 압력과 온도는 배기가스 조건인 300K와 1.0 bar이다.

Table 2:

Input data

2.2 수학적 모델

기상의 유동에 대하여 연속방정식, 운동량 방정식, 에너지 방정식 및 연료증발방정식이 Eulerian형으로 주어지며, 고압축성유동에 대한 k-ε모델이 적용된다. 액상의 유동에 대하여 움직이는 궤적, 운동량, 질량, 에너지 방정식은 Lagrangian형으로 쓰여지며, 각 액적군은 크기, 온도, 속도, 등 모든 성질이 동일한 수천 개의 액적으로 이루어진다. 액상에 대한 기상의 영향은 액상의 방정식에서 전단응력의 항으로 고려되며, 기상에 대한 액상유동의 영향은 기상의 방정식에서 생성항의 형태로 고려된다. 속도/압력쌍의 해석은 PISO 알고리즘을 사용하여 해석된다. 일반좌표계( ξ^l )로 변형된 기상의 전달방정식은 다음과 같이 일반 텐서표시법과 함께 표현된다.

여기에서 Uⁱ는 수직유동항, uⁱ는 속도벡터 $$ \overline{V}$$의 직교좌표성분이며, P_ij는 면적벡터의 직교좌표성분이다.

액체의 질량전달방정식(droplet mass trasfer)은 El Watkil et al. [7]에 의하여 실험과 이론에 의하여 제시된 식 (2)를 이용한다.

여기서 P_t는 전체압력, D는 확산(diffusivity), R_f는 증발연료의 기체상수, T_m은 평균액적표면온도, P_v,∝,P_v,s는 각각 자유공간 및 액적표면에서의 증발연료압력(partial pressure of the fuel vapour far from or at the surface of droplet) 그리고 Sh는 셔우드수를 나타낸다. 본 연구에서 사용한 충돌모델[8]은 W_e넘버에 의존하며, 충돌 후 액적의 법선방향과 수직방향의 속도 및 액적직경은 다음과 같다.

W_e<80인 경우;

W_e>80인 경우;

여기서 하첨자 a, b, d, n, t 는 각각 충돌 후, 충돌 전, 액적의 직경, 충돌면과 수직 및 수평방향을 나타내며, R_xx는 ( 0, 1)사이에서 발생하는 무작위 변수를 나타낸다.

3.1 충돌면이 없는 경우

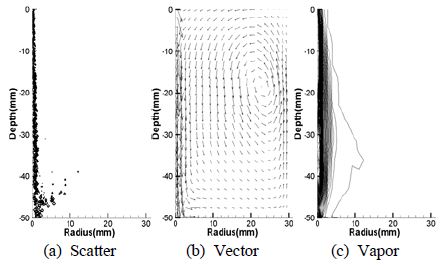
Figure 3은 Figure 3 (a)충돌면의 반경이 0mm(충돌면이 없는 경우)일 때 액적분포 형상, Figure 3 (b)는 벡터분포 형상, Figure 3 (c)는 증발연료의 분포를 나타낸다. 분사액적은 반경방향으로 퍼짐이 극히 제한된 가운데 아랫방향으로만 진행한다.

Figure 3:

Scatter, vector, vapor at no pip

3.2 충돌분무의 액적분포특성

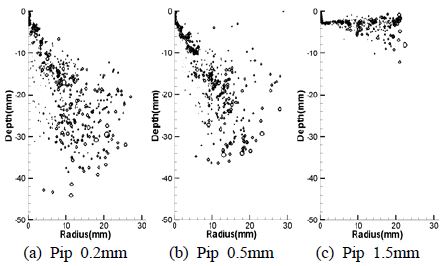
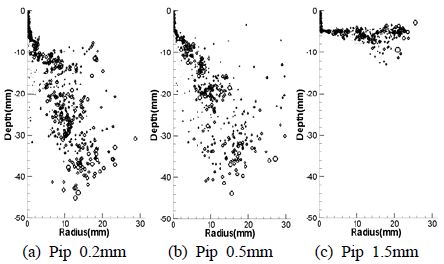
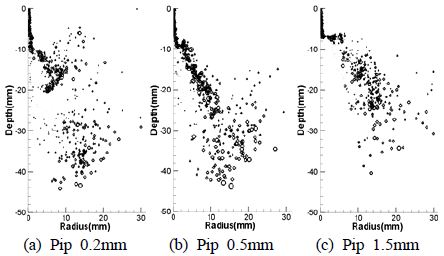
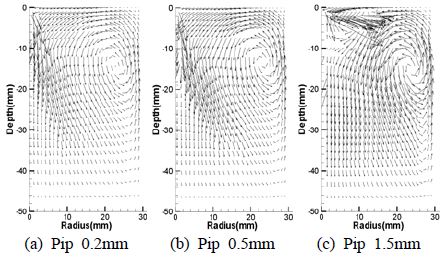
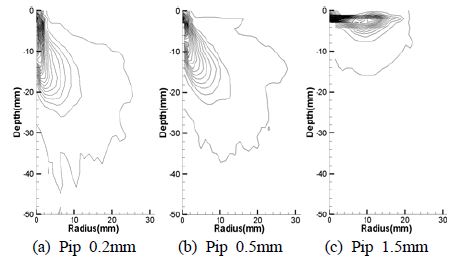
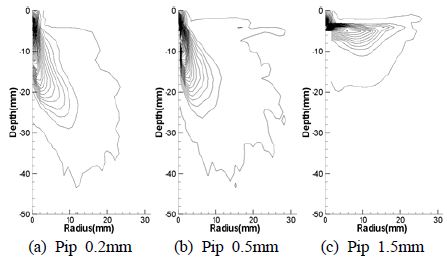
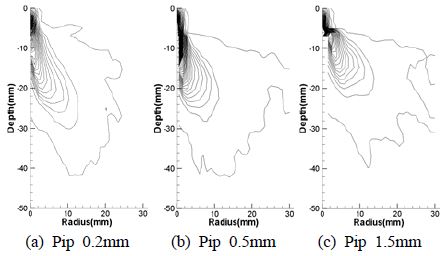
Figure 4는 노즐과 충돌면의 사이거리가 3mm일 때의 액적분포형상을 나타낸다. 충돌면의 반경이 1.5mm인 경우인 Figure 4 (c)에서는 모든 분사 액적이 충돌면에 충돌한 후에 반경방향으로만 퍼져나간다. 충돌면의 반경이 0.2mm인 Figure 4 (b)의 경우는 분사액적의 일부는 충돌면에 충돌한 후에 반경 방향으로 진행하고 일부는 충돌 없이 아래로 내려오는데 이들이 상호작용하여 반경 방향과 깊이 방향으로 액적이 넓게 분포된다. Figure 5는 노즐과 충돌면 사이가 5mm일 때의 액적분포형상을 나타낸다. Figure 5 (a)의 경우 충돌면의 반경이 0.2mm일 때를 나타내며 노즐과 충돌면의 사이거리가 3mm일 때 보다 깊이 방향으로 액적이 조금 더 발달 하였다. Figure 5에서 충돌면의 반경이 증가함에 따라 액적들의 깊이방향 거리가 감소하고 있으며, Figure 5 (c)가 되어서는 충돌면에 충돌한 후 액적들이 완전히 반경방향으로만 퍼져나가고 있다. Figure 6은 노즐과 충돌면의 사이거리가 7mm일 때 액적분포형상을 나타낸다. 충돌면의 반경이 0.2, 0.5mm일 경우 Figure 5와 Figure 6에서 비슷한 액적 분포 형상을 띄고 있지만, Figure 5와 Figure 6 (c)는 노즐과 충돌면 사이의 거리가 5mm에서 7mm로 증가한 액적분포 형상을 나타내고 있으며, 5mm 일 때 반경방향으로만 퍼져나가던 액적들이 거리가 증가함으로써 액적들이 깊이방향으로도 분포되고 있다. 액적분포의 균일성을 살펴보면, 노즐과 충돌면의 거리가 짧은 3 mm인 경우 충돌후의 액적이 균일하게 분포된다. 충돌면의 거리가 증가하면 액적밀집영역이 형성되면서 불균일한 액적분포를 나타낸다.

Figure 4:

Spray distribution in the case of 3mm distance

Figure 5:

Spray distribution in the case of 5mm distance

Figure 6:

Spray distribution in the case of 7mm distance

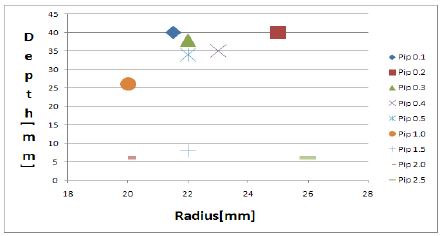
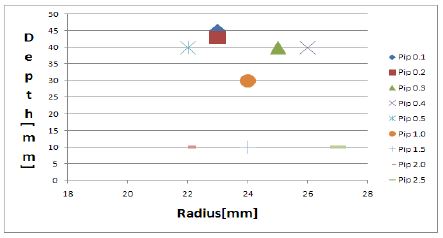
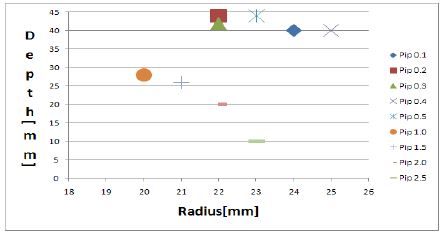
Figure 7은 충돌면의 거리가 노즐에서 3mm인 경우에 충돌면의 반경이 0mm인 경우부터 2.5mm인 경우까지의 반경방향과 깊이방향의 최대 액적 진행거리를 나타낸다. 충돌면의 반경이 0mm(충돌면이 없는 경우)인 경우 깊이 방향 진행거리가 50mm이며, 반경방향 진행거리가 10mm로 대부분 깊이방향으로 분포된다. 충돌면 반경이 0.1mm에서 깊이방향 진행거리는 40mm로 줄어들고 반경방향 진행거리는 20mm로 증가된다. 충돌면 반경이 0.2mm가 되면 깊이방향 진행거리는 40mm로 유지되면서 반경방향 진행거리는 28mm로 크게 증가된다. 충돌반경이 더욱 증가하게 되면 깊이 방향의 진행거리가 크게 줄어들고 반경방향의 진행거리도 줄어드는 경향을 나타낸다. 충돌면이 적당히 마련되면 깊이방향과 반경방향의 액적이 교차하면서 유동의 활성화와 함께 액적분산이 크게 증가하는 특성을 나타낸다. 충돌거리 3mm일 때는 충돌반경 0.2mm가 최적인 것으로 판단된다. Figure 8은 충돌면의 거리가 노즐에서 5mm일 경우이며, Figure 9는 충돌면의 거리가 7mm일 경우를 나타낸다. Figure 8과 Figure 9에서 충돌면의 반경이 0mm인 경우부터 2.5mm인 경우까지의 반경방향과 깊이방향의 최대 액적 진행거리를 나타내고 있으며, 충돌면의 반경이 0mm에서 1.0mm까지는 반경방향으로의 액적분포가 20mm이상, 깊이방향으로의 액적분포가 25mm이상으로 충돌면의 반경이 1.5mm에서 2.5mm일 경우보다 비교적 양호하다. Figure 8에서 충돌면의 반경 1.5, 2.0, 2.5mm일 때 반경방향으로 액적분포는 잘 발달되었지만 깊이방향으로의 액적분포는 미비한 수준이다. Figure 8과 Figure 9에서 충돌면의 반경이 2.5mm일 때 같은 액적분포형상을 나타낸다. 충돌면의 반경이 1.0, 1.5mm일 때 거리가 증가함으로써 깊이방향으로의 액적분포가 증가하였다. 노즐에서 충돌면의 사이거리가 5mm일 때 액적최대발달위치를 보면 충돌면의 반경이 0.4mm가 반경방향과 깊이방향으로 많이 발달 된 것으로 보아 가장 적절하다는 것을 알 수 있고, 충돌면에서 노즐 사이의 거리가 7mm일 때는 충돌면의 반경이 0.5mm가 가장 발달되었다.

Figure 7:

Maximum distance of droplets at distance 3mm

Figure 8:

Maximum distance of droplets at distance 5mm

Figure 9:

Maximum distance of droplets at distance 7mm

3.3 충돌분무의 유동특성

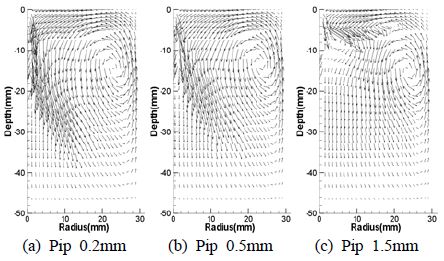
Figure 10은 노즐과 충돌면의 사이거리가 3mm일 때 기체의 속도벡터 분포형상을 나타낸다. 충돌면의 반경이 0.2mm인 Figure 10 (a)의 경우 충돌면이 없는 경우와 비교할 때 반경방향으로 유동이 증가하였다. 충돌면의 반경이 0.5mm인 Figure 10 (b)에서 유동이 더욱 반경방향으로 증가되었으며 충돌면의 반경이 1.5mm인 Figure 10 (c)에서는 아랫방향으로의 유동은 거의 없으며 반경방향으로 강한 유동이 발생함을 알 수 있다. Figure 11과 Figure 12는 노즐과 충돌면의 사이거리가 5mm, 7mm인 경우이며상기에 설명한 Figure 10과 유사하게 반경의 증가와 함께 유동이 반경방향으로 증가되는 경향을 나타낸다.

Figure 10:

Vector distribution in the case of 3mm distance

Figure 11:

Vector distribution in the case of 5mm distance

Figure 12:

Vector distribution in the case of 7mm distance

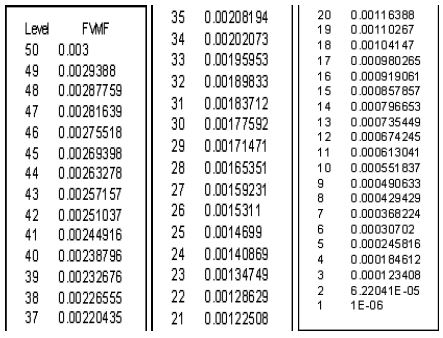
3.4 충돌분무의 증발연료 분포특성

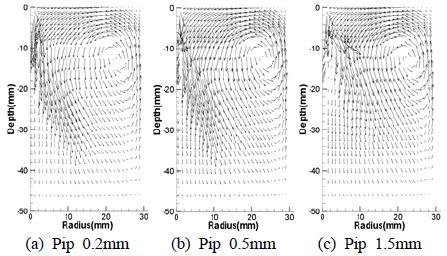
Figure 13은 Figure 14, Figure 15, Figure 16에서 증발연료의 질량분율 값을 나타내는 표이다. Figure 14는 노즐에서 충돌면의 사이거리가 3mm일 때 충돌면의 반경 증가에 따른 증발연료의 질량분율(FVMF : Fuel Volume Mass Fraction) 분포를 나타낸 것이다. 충돌면의 반경이 0.2mm인 Figure 14 (a)의 경우 연료분포가 반경방향으로는 깊이방향으로 갈수록 넓어지고 있으며, 깊이방향으로도 깊이 분포한다. 충돌면의 반경이 0.5mm인 Figure 14 (b)의 경우 0.2mm보다 깊이방향의 길이는 비슷한지만 충돌한 후 비교적 빠르게 반경방향의 분포가 발달하였다. 충돌면의 반경이 1.5mm인 Figure 14 (c)에서는 깊이방향으로 많이 발달되지 못하고 반경방향으로 발달하였다. Figure 15, Figure 16은 노즐에서 충돌면의 사이거리가 5mm, 7mm일 때 연료 분포 형상을 나타낸다. 충돌면의 반경이 0.5mm에서 충돌면의 거리가 짧은 3mm이고 반경이 0.2mm인 경우와 유사한 형태를 나타낸다.

Figure 13:

FVMF (Fuel Volume Mass Fraction) distribution values

Figure 14:

Contour distribution in the case of 3mm distance

Figure 15:

Contour distribution in the case of 5mm distance

Figure 16:

Contour distribution in the case of 7mm distance