Improved transient characteristics of output voltage of marine synchronous generator

1. Introduction

In a power system, voltage stability is an essential element to protect electric and electronic equipment. If the voltage of the power system is not stable, such devices could be frequently damaged due to voltage distortion. In order to keep the quality of a power system high, there is a range of equipment, such as automatic voltage regulators, power system stabilizers and filters, that are available. This paper focuses on the control method used by the automatic voltage regulator of a generator.

Various control methods implemented in the automatic voltage regulators of synchronous generators have been studied. These include PID, PID-combination control, genetic algorithm, slide mode, adaptive-optima control, teaching-learning-based optimization, multi-objective-external optimization, fractionaladaptive control, self-tuning control and neural networks [1]-[20]. In keeping with these studies, this paper demonstrates an improvement in the terminal voltage control of a synchronous generator by neural-networks-(NN) predictive control, compared with that by PID control. Furthermore, it confirms that the proposed control method is superior to other neural-networks methods.

2.Modeling of Synchronous Generator

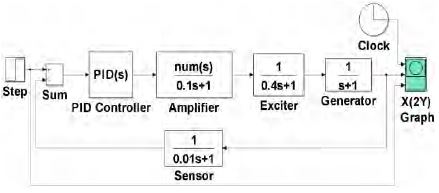
The excitation system of a synchronous generator is composed of an amplifier, an exciter, a generator and a sensor as displayed in Figure 1. Parameters of the transfer function of the system are configured such that k_a= 10 & τ _a= 0.1 for the amplifier, k_e= 0.4 & τ _e= 1 for the exciter, k_g= 1 (depending on the load, this varies from 0.7 to 1.0) & τ _g= 1 for the generator, and k_s= 1 & τ _s= 0.01 for the sensor [10].

Figure 1:

Simulink Model to the Plant with PID

3. Neural Networks Predictive Control

3.2 Structure of Neural Networks

In general, the nonlinear dynamic model equation is determined by the past data of the input and the output as shown in Equation (5).

$\[ \text{y}\left(\text{k+1}\right)\text{=f}\left[\text{y}\left(\text{k}\right)\text{,y}\left(\text{k-1}\right)\text{,…,y}\left(\text{k-n}\right)\text{,u}\left(\text{k}\right)\text{,u}\left(\text{k-1}\right)\text{,…,u}\left(\text{k-m}\right)\right] \]$

(5)

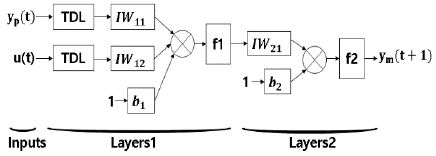
Therefore, in order to train the dynamic model equation using neural networks, a Time Delay Neural Network (TDNN) can be used as shown in Figure 2.

Figure 2:

Structure of Time Delay Neural Networks

Considering the neural-network model, the input and output values of the plant are entered in the input part of the neural network, respectively, and each time-delay value is entered. The output of the neural network must be observed. The output of the neural network configured to learn the plant output value of the next sampling step that is that predictive control function is structured. The learning data necessary for the neural-network learning should be extracted from the results obtained by operating the plant.

The output of the TDNN model is depicted as,

$\[ \widehat{\text{y}}\left(\text{k+1}\right)\text{=bs+}{\sum }_{\text{i=1}}^{\text{N}}{\text{W}}_{\text{2}}\left(\text{1,i}\right)\text{⋅S}\left({\text{X}}_{\text{i}}\right) \]$

(6)

and

$\[ X_i=b\left(i,1\right)+{\sum }_{j=1}^N{w}_1\left(i,j\right)\cdot y\left(k-j+1\right)+{\sum }_{j=1}^N{w}_1\left(i,n+j\right)\cdot y\left(k-j+1\right) \]$

(7)

3.3 Differential equation of a Neural Networks System

Generally, the output derivative for the processor input is calculated in order to apply the control theory,

$\[ \frac{\text{δ}\widehat{\text{y}}\left(\text{k+1}\right)}{\text{δu}\left(\text{k}\right)}\text{=}\frac{\text{δ}}{\text{δu}\left(\text{k}\right)}\left(\text{bs+}{\sum }_{\text{i=1}}^{\text{N}}{\text{W}}_{\text{2}}\left(\text{1,i}\right)\text{⋅S}\left({\text{X}}_{\text{i}}\right)\right) \]$

(8)

Equation (9) can be transformed as follows,

$\[ \frac{\text{δ}\widehat{\text{y}}\left(\text{k+1}\right)}{\text{δu}\left(\text{k}\right)}\text{=}\frac{\text{δ}}{\text{δu}\left(\text{k}\right)}\text{(bs+}{\sum }_{\text{i=1}}^{\text{N}}{\text{W}}_{\text{2}}\left(\text{1,i}\right)\text{⋅S'}\left({\text{X}}_{\text{i}}\right)\frac{\text{δ}{\text{X}}_{\text{1}}}{\text{δu}\left(\text{k}\right)}\text{]} \]$

(9)

Then,

$\[ {\text{S}}^{\text{'}}\text{=}\frac{\text{dS}}{\text{d}{\text{X}}_{\text{i}}} \]$

(10)

$\[ \frac{\text{δ}{\text{X}}_{\text{1}}}{\text{δu}\left(\text{k}\right)}\text{=}\frac{\text{δ}}{\text{δu}\left(\text{k}\right)}\text{b}\left(\text{i,1}\right)\text{+}\frac{\text{δ}}{\text{δu}\left(\text{k}\right)}{\sum }_{\text{j=1}}^{\text{n}}{\text{W}}_{\text{1}}\left(\text{i,j}\right)\text{⋅y}\left(\text{k-j+1}\right)\text{+}\frac{\text{δ}}{\text{δu}\left(\text{k}\right)}{\sum }_{\text{j=1}}^{\text{n}}{\text{W}}_{\text{1}}\left(\text{i,n+j}\right)\text{⋅u}\left(\text{k-j+1}\right) \]$

(11)

Considering y(k − 1), y(k − 2),… y(k − n) values and that u(k − 1), u(k − 2),… u(k − m) are past values that are not influenced by u(k), Accordingly, all summation is zero except for j = 1,

$\[ \frac{\text{δ}{\text{X}}_{\text{1}}}{\text{δu}\left(\text{k}\right)}={\mathrm{W}}_1\left(\text{i,n+1}\right) \]$

(12)

$\[ \frac{\text{δ}\widehat{\text{y}}\left(\text{k+1}\right)}{\text{δu}\left(\text{k}\right)}\text{=}{\sum }_{\text{i=1}}^{\text{N}}{\text{W}}_{\text{2}}\left(\text{1,i}\right)\text{⋅S}\text{'}\left({\text{X}}_{\text{i}}\right)\text{⋅}{\text{W}}_{\text{1}}\left(\text{i,n+1}\right) \]$

(13)

Finally, Equation (12) and Equation (13) is an expression that TDNN neural network represents input & output characteristics. 3.4 Neural-Networks Predictive Control

Predictive control is a method of calculating the control input literally using the predicted value of the system. Therefore, if an appropriate neural-network model is selected and the learning is done well, the neural-network model can express the dynamic characteristics of the actual dynamic system well.

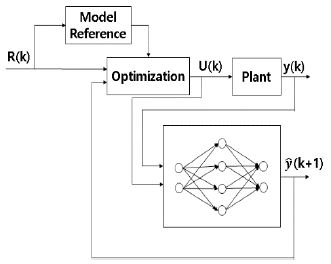
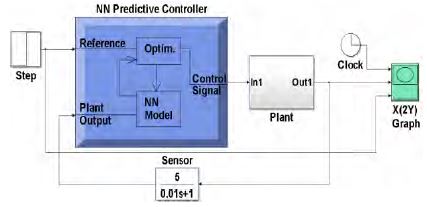
The prediction control algorithm can be constructed using the error between the reference input and the predicted value. Figure 3 is a block diagram illustrating the neural-network predictive control system.

k: Sampling time
r(k): Reference input signal
u(k): Control input value to the plant
y(k) : Output of the plant
e(k): Difference value (Error value) between r(k)& y(k)
$$ \widehat{\text{y}}\left(\text{k+1}\right)$$: Predicted plant output

Figure 3:

Neural-Network Model Predictive Control System

The control input value is calculated using the predicted value rather than the actual output value. By definition, the prediction controller minimizes the objective function J, and the objective function can be composed of error values as follows.

$\[ \text{J=}\frac{\text{1}}{\text{2}}{\text{e}}^{\text{2}}\left(\text{k+1}\right) \]$

(14)

$\[ \mathrm{e}\left(\text{k+1}\right)=\mathrm{r}\left(\text{k+1}\right)-\widehat{y}\left(\text{k+1}\right) \]$

(15)

In order to improve the control performance, this study uses the gradient descent method as follows.

$\[ \text{u}\left(\text{k+1}\right)\text{=u}\left(\text{k}\right)\text{-γ}\frac{\text{δJ}}{\text{δu}\left(\text{k}\right)} \]$

(16)

Using the J value and e(k + 1),

$\[ \frac{\text{δJ}}{\text{δu}\left(\text{k}\right)}\text{=}\frac{\text{1}}{\text{2}}\text{[-2e}\left(\text{k+1}\right)\frac{\text{δ}\widehat{\text{y}}\left(\text{k+1}\right)}{\text{δu}\left(\text{k}\right)}\text{=-e}\left(\text{k+1}\right)\frac{\text{δ}\widehat{\text{y}}\left(\text{k+1}\right)}{\text{δu}\left(\text{k}\right)} \]$

(17)

Considering TDNN,

$\[ \frac{\delta J}{\delta u\left(k\right)}=-e\left(k+1\right){\sum }_{i=1}^n{W}_2\left(1,i\right)\cdot S\text{'}\left(X_1\right)]\times W_1\left(i,n+1\right) \]$

(18)

$\[ \text{u}\left(\text{k+1}\right)\text{=u}\left(\text{k}\right)\text{+γe}\left(\text{k+1}\right)\left[{\sum }_{\text{i=1}}^{\text{n}}{\text{W}}_{\text{2}}\left(\text{1,i}\right)\text{⋅S}\text{'}\left({\text{X}}_{\text{i}}\right)\text{⋅}{\text{W}}_{\text{1}}\left(\text{i,n+1}\right)\right] \]$

(19)

The scalar values may be represented by prediction vectors as follows.

$\[ \text{R=}\left[\text{r}\left(\text{k+1}\right)\text{,r}\left(\text{k+2}\right)\text{,…,r}\left(\text{k+T}\right)\right] \]$

(20)

$\[ {\mathrm{Y}}_{\mathrm{e}}=\left[\widehat{y}\left(\text{k+1}\right)\text{,}\widehat{y}\left(\text{k+2}\right)\text{,…,}\widehat{y}\left(\text{k+T}\right)\right] \]$

(21)

$\[ \text{U=}\left[\text{u}\left(\text{k}\right)\text{,u}\left(\text{k+1}\right)\text{,…,u}\left(\text{k+T-1}\right)\right] \]$

(22)

$\[ \text{E=}\left[\text{e}\left(\text{k+1}\right)\text{,e}\left(\text{k+2}\right)\text{,…,u}\left(\text{k+T}\right)\right] \]$

(23)

By definition, the prediction controller minimizes the objective function J, and the objective function can be expressed in terms of error values as follows,

$\[ \text{J=}\frac{\text{1}}{\text{2}}\left[\text{E⋅}{\text{E}}^{\text{T}}\right] \]$

(24)

To update the control performance, the gradient descent method is used as follows,

$\[ \text{U}\left(\text{k+1}\right)\text{=U}\left(\text{k}\right)\text{-γ}\frac{\text{δJ}}{\text{δU}\left(\text{k}\right)} \]$

(25)

$\[ \frac{\text{δJ}}{\text{δU}\left(\text{k}\right)}\text{=-E}\frac{\text{δ}{\text{Y}}_{\text{e}}}{\text{δU}\left(\text{k}\right)} \]$

(26)

The Jacobian matrix $$ \frac{\text{δ}{\text{Y}}_{\text{e}}}{\text{δU}\left(\text{k}\right)}$$ is obtained as follows,

$\[ \frac{\text{δ}{\text{Y}}_{\text{e}}}{\text{δU}\left(\text{k}\right)}\text{=}\begin{array}{ccc}\frac{\text{δ}\widehat{\text{y}}\left(\text{k+1}\right)}{\text{δu}\left(\text{k}\right)}& \text{0}& \text{0}\\ \frac{\text{δ}\widehat{\text{y}}\left(\text{k+2}\right)}{\text{δu}\left(\text{k}\right)}& \frac{\text{δ}\widehat{\text{y}}\left(\text{k+2}\right)}{\text{δu}\left(\text{k+1}\right)}& \text{0}\\ \frac{\text{δ}\widehat{\text{y}}\left(\text{k+T}\right)}{\text{δu}\left(\text{k}\right)}& \frac{\text{δ}\widehat{\text{y}}\left(\text{k+T}\right)}{\text{δu}\left(\text{k+1}\right)}& \frac{\text{δ}\widehat{\text{y}}\left(\text{k+T}\right)}{\text{δu}\left(\text{k+T-1}\right)}\end{array} \]$

(27)

4. Simulation and result

4.1 PID control simulation and the result

Firstly, each gain of the PID control through the Ziegler Nichols tuning method in Figure 1 was measured as Kcr : 1.702, Pcr : 1.08, Kp : 0.54, Ti = 0.54 and Td = 0.135 as shown in Figure 4.

Figure 4:

PID control with the Ziegler Nichols tuning method

Secondly, PID controller parameters were acquired as 0.172486 for P gain, 0.167368 for I gain, 0.020729 for D gain and 5.172102 for the filter coefficient (N) using the automatic tuning method.

The compensator formula is given as follows,

$\[ \text{P+I}\frac{\text{1}}{\text{s}}\text{+D}\frac{\text{N}}{\text{1+N}\frac{\text{1}}{\text{s}}} \]$

(28)

As shown in Figure 5, automatic tuning of the PID control of the synchronous generator resulted in values of 0.863 s for the rise time, 3.08 s for the settling time, and 8.23% for the overshoot being obtained.

Figure 5:

PID auto-tuning control of the automatic voltage regulator

4.2 NN Predictive control simulation and the result

The Simulink Model of the plant in Figure 6 includes the same transfer functions of a synchronous generator.

Figure 6:

Plant Model with NN Predictive Controller

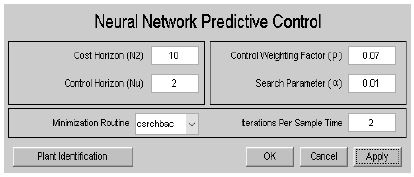
The parameter input for the NN predictive controller was set as in Figure 7. N2 of cost horizon enters 10 for time steps that predicted errors are minimum. ρ, Nu of control horizon, is 2 that control increasement values are minimized. The search parameter was 0.001 for the determination of the line search. The minimization routine used was csrchbac.

Figure 7:

Parameter input window of the NN Predictive Controller

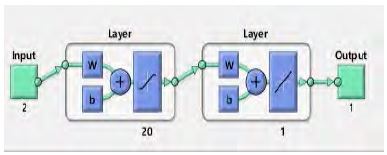
The synchronous generator plant model network was 20 at the first layer as seen in Figure 8. The training function was trainlm which refers to Levenberg-Marquardt. Furthermore, the objective function was Mean Square Error.

Figure 8:

Input window for the Plant Identification

As shown in Figure 9, after training the neural-networks predictive control, the configuration was obtained.

Figure 9:

Configuration of Neural Networks

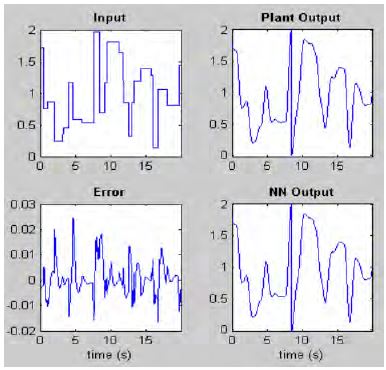
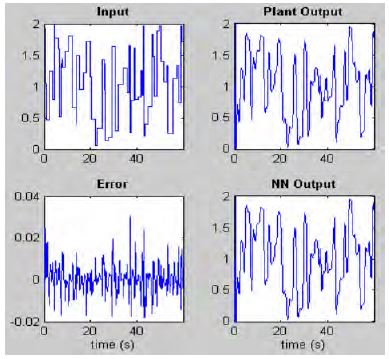
Following the completion of the training of the system, training performance could be comparatively shown between Figure 10 and Figure 11.

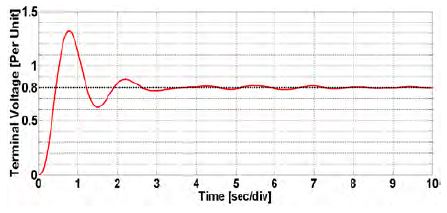
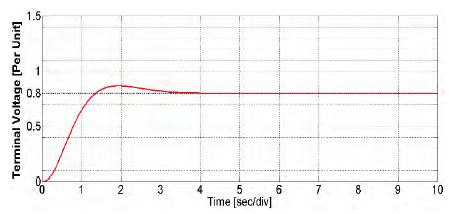
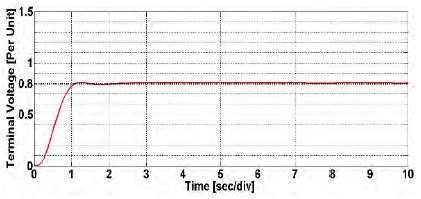
By using NN predictive control in a synchronous generator, the result in Figure 12 was acquired. Through the proposed control method, 0.58 s for the rise time, 1.02 s for the settling time, and 0.23% for the overshoot on the system were obtained.

Figure 10:

Validation data for the NN Predictive Control

Figure 11:

Training data for the NN Predictive Control

Figure 12:

Results of NN Predictive Control

5. Conclusion

Frequent changes in voltage cause damage to electric and electronic devices through switching loss and thermal loss. Therefore, maintaining the specified voltage in a power system is important. A range of equipment, such as automatic voltage regulators, power system stabilizers and filters, can be used to keep the voltage of a power system stable.

This paper dealt with the control method of the automatic voltage regulator of a synchronous generator. To verify the validity of the proposed method, the results obtained were compared with those obtained using PID control.

Following computer simulations, the terminal voltage from PID control is measured with 0.863 s for the rise time, 3.08 s for the settling time, and 8.23% for the overshoot. The proposed method measured 0.58 s for the rise time, 1.02 s for the settling time, and 0.23% for the overshoot. Through the use of the proposed control method, therefore, output voltage was improved 48% for rise time and 3.02 times for setting time and 10% for overshoot. This paper verified that the output voltage of the synchronous generator using neural-networks predictive control can be improved compared to that obtained using PID control.

Acknowledgments

This work was supported by the Korea Maritime And Ocean University Research Fund.

References

• L. D. S. Coelho, “Tuning of PID controller for an automatic regulator voltage system using chaotic optimization approach”, Chaos, Solitons & Fractals, vol. 39(no. 4), p1504-1514, (2009).
• S. Kansit, and W. Assawinchaichote, “Optimization of PID controller based on PSOGSA for an automatic voltage regulator system”, Procedia Computer Science, vol. 86, p87-90, (2016). [https://doi.org/10.1016/j.procs.2016.05.022]
• H. Shayeghi, A. Younesi, and Y. Hashemi, “Optimal design of a robust discrete parallel FP+FI+FD controller for the Automatic Voltage Regulator system”, International Journal of Electrical Power & Energy Systems, vol. 67, p66-75, (2015). [https://doi.org/10.1016/j.ijepes.2014.11.013]
• S. Panda, B. K. Sahu, and P. K. Mohanty, “Design and performance analysis of PID controller for an automatic voltage regulator system using simplified particle swarm optimization”, Journal of the Franklin Institute, vol. 349(no. 8), p2609-2625, (2012). [https://doi.org/10.1016/j.jfranklin.2012.06.008]
• F. Naeim, and T. Bingqi, “Application of self-tuning PID controller on the AVR system”, Proceedings of 2012 IEEE international Conference on Mechatronics and Automation, p2510-2514, (2012).
• J. H. Abdullah, M. A. Kaml, K. J. Mahmoud, and M. W. Mustafa, “Integrated PLC-fuzzy PID Simulink implemented AVR system”, International Journal of Electrical Power & Energy Systems, vol. 69, p313-326, (2015).
• I. Szuvovivski, T. S. P. Fernandes, and A. R. Aoki, “Simultaneous allocation of capacitors and voltage regulators at distribution networks using Genetic Algorithms and Optimal Power Flow”, International Journal of Electrical Power & Energy Systems, vol. 40(no. 1), p62-69, (2012). [https://doi.org/10.1016/j.ijepes.2012.02.006]
• S. Panda, and K. Y. Narendra, “Automatic generation control of multi-area power system using multi-objective nondominated sorting genetic algorithm-II”, International Journal of Electrical Power & Energy Systems, vol. 53, p54-63, (2013). [https://doi.org/10.1016/j.ijepes.2013.04.003]
• A. G. Suri babu, and B. T. Chiranjeevi, “Implementation of fractional order PID controller for an AVR system using GA and ACO optimization techniques”, IFAC-PapersOnLine, vol. 49(no. 1), p456-461, (2016).
• A. A. EL Ela, and S. R. Spea, “Optimal corrective actions for power systems using multi-objective genetic algorithms”, Electric Power Systems Research, vol. 79(no. 5), p722-733, (2009).
• R. L. A. Ribeiro, C. M. S. Neto, F. B. Costa, T. O. A. Rocha, and R. L. Barreto, “A sliding-mode voltage regulator for salient pole synchronous generator”, Electric Power Systems Research, vol. 129, p178-184, (2015). [https://doi.org/10.1016/j.epsr.2015.07.016]
• L. B. Prasad, H. O. Gupta, and B. Tyagi, “Application of policy iteration technique based adaptive optimal control design for automatic voltage regulator of power system”, International Journal of Electrical Power & Energy Systems, vol. 63, p940-949, (2014). [https://doi.org/10.1016/j.ijepes.2014.06.057]
• S. Chatterjee, and V. Mukherjee, “PID controller for automatic voltage regulator using teaching-learning based optimization technique”, International Journal of Electrical Power & Energy Systems, vol. 77, p418-429, (2016). [https://doi.org/10.1016/j.ijepes.2015.11.010]
• V. Rajinikanth, and S. C. Satapathy, “Design of controller for automatic voltage regulator using teaching learning based optimization”, Procedia Technology, vol. 21, p295-302, (2015). [https://doi.org/10.1016/j.protcy.2015.10.032]
• G. Q. Zeng, J. Chen, Y. X. Dai, L. M. Li, C. W. Zheng, and M. R. Chen, “Design of fractional order PID controller for automatic regulator voltage system based on multi-objective extremal optimization”, Neurocomputing, vol. 160, p173-184, (2015). [https://doi.org/10.1016/j.neucom.2015.02.051]
• N. Aguila-Camacho, and M. A. Duarte-Mermoud, “Fractional adaptive control for an automatic voltage regulator”, ISA Transactions, vol. 52(no. 6), p807-815, (2013). [https://doi.org/10.1016/j.isatra.2013.06.005]
• M. Asama, H. Ukai, M. Sone, and K. Nakamura, “DSPBASED H∞ controlled Digital Automatic Voltage Regulator for use on Engine Generator”, IFAC Proceedings Volumes, vol. 35(no. 1), p283-288, (2002). [https://doi.org/10.3182/20020721-6-es-1901.00381]
• M. Fasai, K. J. Zachariah, and J. W. Finch, “Implementation of a self-tuning AVR, IEE Proceedings of Control Theory Application”, vol. 144(no. 1), p32-39, (1997).
• H. Gozde, and M. C. Taplamacioglu, “Comparative performance analysis of artificial bee colony algorithm for automatic voltage regulator (AVR) system”, Journal of the Franklin Institute, vol. 348(no. 8), p1927-1946, (2011). [https://doi.org/10.1016/j.jfranklin.2011.05.012]
• L. N. Magangane, and K. A. Folly, “Neuro-controllers for Synchronous Generator”, Proceedings of the 19th World Congress The International Federation of Automatic Control, p8218-8222, (2014). [https://doi.org/10.3182/20140824-6-za-1003.00768]
• B. R. Lee, Fuzzy Neural Network Focusing on Matlab/Simulink, UUP, p211-217, (2012), (in Korean).