퍼지 외란 추정기를 이용한 선박의 퍼지 PID형 오토파일럿 및 항로 추종

1. 서 론

선박을 운항함에 있어서 정확한 항로 추종은 최단시간에 목적지에 도착하게 하며 또한 운항 중 발생하는 추진에너지의 손실을 최소화 시켜 경제적인 운항에 필수적이며 선박자동화의 목적에 부합한다. 선박 자동화를 위해서는 첫 번째, 항로를 결정할 수 있는 항로 결정 알고리즘과 두 번째, 결정된 항로를 선박이 제대로 추종할 수 있도록 하는 가이던스 시스템, 마지막으로 가이던스 시스템의 명령에 따라 선박을 제어하는 오토파일럿 시스템이 필요하다[1][2]. 선박을 제어하는 오토파일럿 시스템은 정확하고 빠른 변침 능력을 가져야 하며 큰 회두각 변화에 대한 오버슈트를 발생시키지 않아야 한다. 또한 조타각의 변화가 거칠게 일어나는 것을 방지해 불필요한 에너지 손실을 줄일 수 있어야 하며 비선형성이 강한 경우에서도 정상상태 오차를 가지지 않아야 한다. 본 논문에서는 이와 같은 조건을 충족시킬 수 있는 속도형 퍼지 PID제어기 오토파일럿을 기본으로 적용하고자 한다. 그러나 속도형 퍼지 PID형 오토파일럿 시스템을 사용한다 하더라도 선박 외부에서 미지의 외란이 인가되면 선박은 정해진 항로를 유지할 수 없다. 이와 같은 문제를 해결하기 위해서 본 논문에서는 이노베이션 프로세스의 특성을 이용하여 미지의 외란 존재여부를 판단하고, 미지의 외란의 존재가 판단되었으면 Kalman 필터 기반의 퍼지 외란 추정기를 통해 선박에 미치는 미지의 외란의 영향을 제거시켜주는 제어시스템을 제안한다. 제안한 제어시스템의 성능을 확인하기 위해서 시뮬레이션을 실시하고 시뮬레이션 결과를 바탕으로 제안한 방법의 성능과 유효성을 검증한다.

2. 속도형 퍼지 PID 제어기 오토파일럿

2.2 속도형 퍼지 PID제어기와 PD제어기 성능 비교

본 논문의 오토파일럿 제어기로서 기본적으로 채택한 퍼지 PID 제어기의 성능을 검증하기 위하여 기존의 PD 제어기와 비교하는 시뮬레이션을 수행하였다. 시뮬레이션에 사용된 선박의 제원은 Table 1이과 같다.

$\[ \delta =-K_p\left({\psi }_d-\psi \right)+K_{d}r \]$

(2)

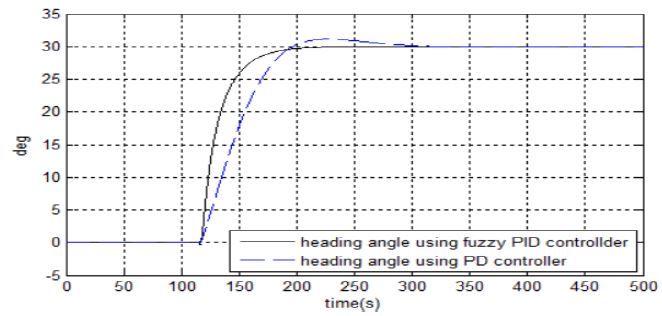
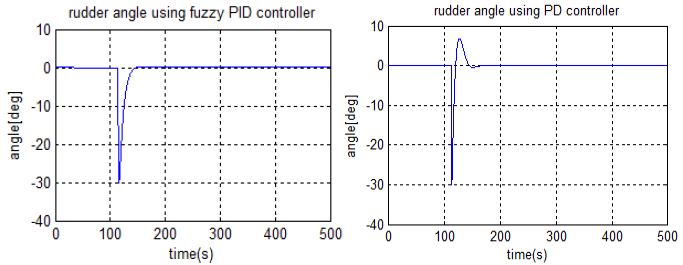
식 (2)는 PD형 오토파일럿으로 K_p = 1, K_d = 70로 최적설정하였고 ψ_d 및 ψ는 기준 회두각과 선박에서 측정된 회두각을 의미하고 r은 측정된 회두각속도이다. Figure 1 및 Figure 2는 퍼지 PID 제어기와 PD 제어기로 구성된 오토파일럿을 이용하여 선박의 회두각과 조타각을 비교한 시뮬레이션이다. 조타각은 30^∘로 설정하였다. Figure 1에서 나타난 것처럼 PD 제어기를 이용하면 오버슈트가 발생하고 기준 회두각까지 정착시간도 퍼지 PID 제어기형에 비해 상대적으로 길어진다. 이와 같이 빠른 변침을 하지 못하기 때문에 선박이 항로에서 벗어나게 된다. 그리고 Figure 2는 조타 명령각을 나타낸 시뮬레이션 결과이다.

Figure 1:

Comparison of heading angles using fuzzy PID controller and PD controller

Figure 2:

Comparison of rudder angles using fuzzy PID controller and PD controller

퍼지 PID 제어기를 이용하면 조타각의 변화가 부드럽게 나타나는 반면 PD 제어기는 거칠게 나타나 선박의 에너지 손실을 증가시킨다. 시뮬레이션을 통해 퍼지 PID 제어기의 성능을 검증하였으며 본 논문에서는 오토파일럿 제어기로서 속도형 퍼지 PID 제어기를 적용하였다.

3. 제어시스템 구성방법

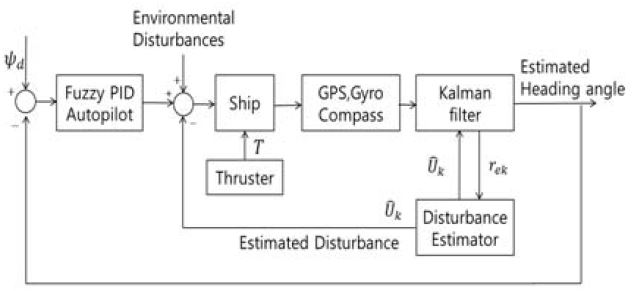
본 논문에서 제안하는 회두각 유지 제어를 위한 선박의 제어시스템 구성 개념은 Figure 3과 같다.

Figure 3:

Control structure for ship control system

선박의 항로가 결정되면 그에 따른 기준 회두각도 결정된다. 이때 기준 회두각을 유지할 수 있도록 퍼지 PID형 오토파일럿에서 조타각을 계산한 뒤 계산된 조타각이 선박모델의 입력으로 들어가 선박의 회전운동이 발생한다. 그리고 선박의 전진운동은 프로펠러 추력 T에 의해 이루어진다. 그러나 아무리 적응성이 뛰어난 퍼지 PID형 오토파일럿을 사용한다 하더라도 운항중에 선박외부에서 미지의 외란이 인가된다면 선박에 x₀, y₀방향에 대한 힘과 z₀축에 대한 모멘트가 추가되어 선박은 정해진 항로를 벗어나게 된다. 이와 같은 문제를 해결하기 위해 Kalman 필터의 이노베이션 특성을 이용하여 해류, 파도, 바람으로 인해 선박운동을 방해하는 미지의 외란의 존재여부를 판단하고, 미지의 외란의 존재가 판단되면 퍼지 외란 추정기를 통해 미지의 외란의 크기를 추정하고 이를 피드백 시켜 미지의 외란의 영향을 상쇄시켜 주고자 한다. 제안한 방법을 적용한다면 미지의 외란으로 인해 선박에 추가되는 힘과 모멘트를 상쇄시켜 주는 효과를 가지게 되어 선박이 정해진 항로를 크게 벗어나지 않고 운항을 할 수 있게 된다. 여기서, r_ek는 이노베이션을 의미하고 $$ {\widehat{U}}_k$$은 미지의 외란 추정값으로서 이들에 대한 정의와 설명은 6장에서 상세히 설명한다.

4. 선박 모델

선박의 운동방정식은 6자유도 운동방정식으로 구성되며 이를 식으로 나타내면 식 (3)과 같다[7].

여기서, M은 관성행렬, C는 Coriolis 행렬, D는 감쇠행렬, τ는 선박이 운항하는데 필요한 추력과 타력을 포함한 힘과 모멘트를 의미한다. 벡터 ν = [u,υ,w,p,q,r]^T로 정의되며 각각의 요소들은 x, y, z축의 속도와 각속도이다. τ_disturbance는 τ_current + τ_waυe + τ_wind로 구성되며 외란으로 작용하는 해류, 파도, 바람의 힘과 모멘트의 합이다. 본 논문에서는 선박이 운항중에 외란으로 작용하는 대표적인 3가지 해류, 파도, 바람을 적용하여 실제와 유사한 환경을 만들었다. 선박이 운항하는데 있어서는 x₀, y₀축 방향으로의 운동과 z₀축에 대한 회전운동만 생각해도 무방하기 때문에 4.1절과 같이 surge, sway, yaw로 구성된 3자유도 선박모델을 이용하였다. x₀, y₀, z₀는 선박 좌표계에서의 x, y, z방향을 의미한다.

5. 해류, 바람, 파도의 영향을 받는 선박모델

5.1 해류 모델

5.1.1 해류 생성

해류생성은 1차 Gauss-Markov 프로세스를 사용하며 해류의 평균속도 V_c(t) [m/s]는 식 (13)과 같다[8].

$\[ {\dot{V}}_c\left(t\right)+{\mu }_0{V}_c\left(t\right)=w\left(t\right) \]$

(13)

여기서, w(t)는 평균이 0인 백색 가우시간 잡음이며, μ₀는 0보다 크거나 같은 값을 가지는데 통상적으로 0을 선정한다. 해류의 평균속도를 실제와 비슷한 환경을 만들어주기 위해 V_min ≤ V_c(t) ≤ V_max과 같이 일정 범위를 설정하고 식 (14)와 같이 오일러 적분을 통해서 해류를 생성한다.

(14)

여기서, h는 샘플링 시간, V_min, V_max는 해류 평균속도의 최소값과 최대값이다.

5.1.2 해류가 선박에 미치는 영향

지구 고정좌표계에서 해류의 평균 속도 V_c와 해류방향 β[deg]는 Figure 4와 같이 정의되며 선박 이동 좌표계에서 해류의 속도 u_c, υ_c가 선박에 미치는 영향은 식 (15)와 같다.

Figure 4:

Definition of average velocity Vc and direction β of the current for a ship

$\[ \begin{array}{c}{u}_c=V_c\cos \left(\beta -\psi \right)\\ {\upsilon }_c=V_c\sin \left(\beta -\psi \right)\end{array} \]$

(15)

5.2 파도모델

5.2.1 파도의 상태공간 방정식

PM(Perison-Moskowitz) 스펙트럼 밀도 함수를 상태공간 방정식으로 표현하기 위한 수단으로 선형근사시킨 파워 스펙트럼 밀도 함수 P_yy(ω)는 w₁(s) 가 입력일 때 출력으로 만들어지며 식 (16)은 파도의 상태공간방정식이다[9][10].

$\[ \begin{array}{c}\left[\begin{array}{c}\dot{{\psi }_H}\\ \dot{{\xi }_H}\end{array}\right]=\left[\begin{array}{cc}-{\omega }_0^2& -2\text{λ}{\omega }_0\\ 0& 1\end{array}\right]\left[\begin{array}{c}{\psi }_H\\ {\xi }_H\end{array}\right]+\left[\begin{array}{c}{K}_w\\ 0\end{array}\right]w_1\\ y=\left[\begin{array}{cc}1& 0\end{array}\right]\left[\begin{array}{c}{\psi }_H\\ {\xi }_H\end{array}\right]\end{array} \]$

(16)

여기서, ω₀는 파도의 주파수[rad/s], λ는 댐핑계수, w₁는 평균이 0인 백색 가우시안 잡음을 의미한다. K_w는 이득으로 2λω₀σ_w로 이루어진다. σ_w는 파도의 밀도를 설명하는 상수로 파워 스펙트럼 밀도 함수 P_yy(ω) 가 최대값을 가질 때의 주파수를 이용하여 구한다. 이를 식 (17)과 같이 표현할 수 있다.

$\[ {\max P_{yy}\left(\omega \right)|}_{\omega ={\omega }_0}={\sigma }_w^2 \]$

(17)

5.2.2 파도가 선박에 미치는 영향

파도의 주파수ω₀가 선박에 인가될 경우 실제 선박에 영향을 주는 파도의 주파수는 회두각에 따라 변하게 되는데 이를 나타내면 식 (18)과 같다[10].

$\[ {\omega }_e\left(U,{\omega }_0,\alpha \right)={\omega }_0-\frac{{\omega }_0^2}{g}U\cos \alpha \]$

(18)

여기서, ω_e는 실제 선박에 인가되는 파도의 주파수[rad/s], U는 선박의 전진방향 속도[m/s], α는 회두각과 파도의 방향 사이의 각도[deg]를 의미하며 Figure 5와 같이 정의한다.

Figure 5:

Definition of angle α

5.4절에서 실제 선박에 인가되는 주파수 ω_e를 사용하여 파도모델을 반영하였다.

5.3 바람 모델

5.3.1 바람 생성

바람 V_R 을 생성하는 방법은 식 (19)로 이루어진다[10].

$\[ \begin{array}{c}\dot{x_1}=w_2\\ \dot{x_2}=-\frac{1}{D}\left(x_2-K{w}_3\right)\\ V_R=x_1+x_2\end{array} \]$

(19)

여기서, w₂ , w₃는 백색 가우시안 잡음을 의미하며 K는 시간에 대한 상수, D는 이득에 대한 상수 값으로 $$ K=\sqrt{5286k{V}_R\left(10\right)}$$며 $$ D=\sqrt{286/V_R\left(10\right)}$$으로 주어진다. V_R(10)은 해수면을 기준으로 바람이 10m 위에서 부는 바람의 속도[knots]를 의미하며 k는 교란 요소로서 0.05의 값을 가진다고 가정한다.

5.3.2 바람이 선박에 미치는 영향

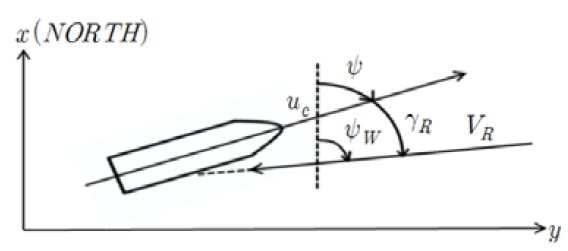
τ_wind는 [X_wind, Y_wind, N_wind]^T 로 이루어지며 각각의 구성요소들은 바람의 힘과 모멘트를 의미한다. 여기서, X_wind, Y_wind, N_wind는 식 (20)으로 이루어지며 V_R은 바람의 속도, ψ_W는 바람의 각도[deg], γ_R은 선박에 미치는 바람의 각도[deg]이며 Figure 6에 이를 나타내었다[11].

Figure 6:

Definition of wind speed VR and direction γR

$\[ \begin{array}{c}{X}_{wind}=\frac{1}{2}{C}_X\left({\gamma }_R\right){\rho }_w{V}_R^2{A}_T\\ Y_{wind}=\frac{1}{2}{C}_Y\left({\gamma }_R\right){\rho }_w{V}_R^2{A}_L\\ N_{wind}=\frac{1}{2}{C}_N\left({\gamma }_R\right){\rho }_w{V}_R^2{A}_{L}L\end{array} \]$

(20)

여기서, C_X, C_Y는 바람의 힘에 대한 계수를, C_N은 바람의 모멘트에 대한 계수를 의미하며 C_X, C_Y, C_N은 식 (21)과 같다. 그리고 ρ_w는 공기밀도[kg/m³]를 의미한다.

$\[ \begin{array}{c}{C}_X=A_0+A_1\frac{2A_L}{L^2}+A_2\frac{2A_T}{B^2}+A_3\frac{L}{B}+A_4\frac{S}{L}+A_5\frac{C}{L}+A_{6}M\\ C_Y=B_0+B_1\frac{2A_L}{L^2}+B_2\frac{2A_T}{B^2}+B_3\frac{L}{B}+B_4\frac{S}{L}+B_5\frac{C}{L}+B_6\frac{A_{SS}}{A_L}\\ C_N=C_0+C_1\frac{2A_L}{L^2}+C_2\frac{2A_T}{B^2}+C_3\frac{L}{B}+C_4\frac{S}{L}+C_5\frac{C}{L}\end{array} \]$

(21)

여기서, A_i, B_i(i = 0...6) C_j(j = 0...5) 에 해당하는 파라미터 값들과 나머지 8개의 파라미터 값들은 기존의 연구의 값을 참고 하였다[11].

6. Kalman 필터 기반의 퍼지 외란 추정기 알고리즘

선형화된 오토파일럿 선박모델의 시스템에서 외부로부터 해류, 파도, 바람과 같은 미지의 외란이 인가되는 경우 Kalman 필터는 선박의 운동상태를 정확히 추정할 수 없다. 이를 보정하기 위해서 이노베이션 프로세스의 특성을 이용하여 미지의 외란의 존재여부를 판단하고 그 크기를 추정하는 퍼지 외란 추정기법을 적용한다[12][13].

6.1 미지의 외란 존재 판단방법

미지의 외란의 영향으로 DC성분을 가지고 변하는 이노베이션 프로세스는 평균 0부근을 유지하지 못하므로 매 샘플링 시간마다 이노베이션 프로세스 값을 절대값으로 환산하고 특정한 수의 샘플링 구간동안 더한다면 크게 변하지 않는 값 식 (24)를 얻을 수 있다[13].

$\[ S=\left(\sum _{i=0}^N\left|r_{ek-i}\right|\right)/N, i=\mathrm{0,1},\dots ,N \]$

(24)

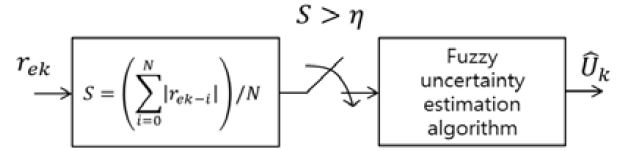
여기서, r_ek는 샘플링 시간 k에서 발생하는 kalman 필터의 이노베이션 프로세스이고 N은 축적하고자 하는 데이터 개수의 범위를 정하는 윈도우로 N값이 너무 크면 r_ek가 S에 큰 영향을 주지 않아 최신정보에 둔감해 지며 너무 작으면 r_ek가 S에 큰 영향을 주기 때문에 최신정보에 민감해진다. 따라서 N의 크기는 설계자가 민감도를 판단하여 적절하게 결정한다. 식 (24)에서 계산된 S값을 바탕으로 미지의 외란의 존재 여부를 판단하는 것은 Figure 7과 같다.

Figure 7:

Test for uncertainty presence using innovation process

여기서, η는 문턱값으로 정의되는 상수로 S값을 토대로 설계자가 직접 결정하는 것이며 S>η조건을 만족 하는 경우 시스템에 미지의 외란이 인가되는 경우라 판단하고 퍼지 불확실성 추정 알고리즘에서 미지의 외란의 크기를 추정하여 추정값 $$ {\widehat{U}}_k$$를 출력하게 된다.

6.2 퍼지 불확실성 추정 알고리즘

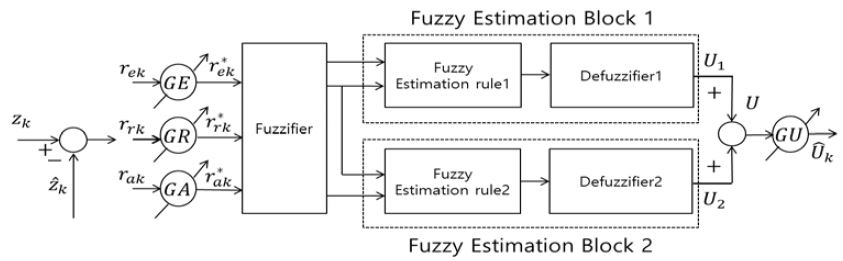
6.1절에서 선박 외부에서 미지의 외란이 인가될 때 미지의 외란 존재 여부를 판단하는 방법을 통해 미지의 외란의 존재를 판단하고 존재가 판단되었으면 이를 추정하기 위한 퍼지 불확실성 추정 알고리즘은 Figure 8과 같고 사용되는 변수들은 식 (25)로 정의된다. 여기서, T는 샘플링 시간, r_rk는 이노베이션 프로세스를 시간T로 나눈 값, r_ak는 r_rk의 변화율이다. GE,GR,GA는 각각 r_ek, r_rk, r_ak의 크기를 정규화 시키기는 입력 스케일 파라미터, GU는 퍼지 출력 U를 위한 스케일 파라미터, L은 입력과 출력 퍼지집합을 정규화 시키는 정규화 파라미터로 L은 설계자가 직접 결정한다. 퍼지 불확실성 추정 알고리즘의 입력 r_ek^*, r_rk^*, r_ak^*를 퍼지 집합으로 퍼지화시키고 퍼지 추정 규칙과 비퍼지화 과정을 거쳐 U₁, U₂가 생성된다[14]. 비퍼지화를 통해 생성된 출력 U₁, U₂를 더하고, GU를 곱하면 미지의 외란 추정값 $$ {\widehat{U}}_k$$가 생성되며 $$ {\widehat{U}}_k$$는 식 (26)과 같다.

Figure 8:

Functional diagram of an uncertainty estimation algorithm

$\[ \begin{array}{cc}{r}_{ek}=z_k-\widehat{z_k}& r_{ek}^{*}=GE\times r_{ek}\\ r_{rk}=r_{ek}/T& r_{rk}^{*}=GR\times r_{rk}\\ r_{ak}=\left[r_{ek}-r_{ek-1}\right]/T& r_{ak}^{*}=GA\times r_{ak}\\ GE=L/\left|r_{ek}\right|& GR=L/\left|r_{rk}\right|\\ GA=L/\left|r_{ak}\right|& GU=L/GR\\ U=U_1+U_2& {\widehat{U}}_k=U\times GU\end{array} \]$

(25)

$\[ {\widehat{U}}_k=K_i{r}_{ek}+K_p{r}_{rk}+K_d{r}_{ak} \]$

(26)

여기서, K_i, K_p,K_d는 식 (27)과 같다.

$\[ \begin{array}{c}{K}_i=0.5\times GU\times GE\\ K_p=0.5\times GU\times GR\\ K_d=0.25\times GU\times GA\end{array} \]$

(27)

미지의 외란 추정값 $$ {\widehat{U}}_k$$를 식 (22)의 해류, 파도, 바람이 포함된 선박모델에 피드백 시켜 미지의 외란을 상쇄시키는 것을 식으로 나타내면 식 (28)과 같다.

$\[ \begin{array}{c}{\text{x}}_k=A{\text{x}}_{k-1}+B{u}_{k-1}+D{w}_{k-1}+\left(U_{k-1}-{\widehat{U}}_{k-1}\right)\\ z_k=C{x}_k+{\upsilon }_k\end{array} \]$

(28)

$$ {\widehat{U}}_k$$가 정상적으로 추정이 된다면 식 (28)과 같이 미지의 외란으로 선박에 추가되는 힘과 모멘트의 영향을 상쇄시켜 선박이 정해진 항로를 크게 벗어나지 않고 운항할 수 있을 것이라 판단할 수 있다.

7. 시뮬레이션

시뮬레이션에 적용한 선박모델은 식 (22)이고, 선박은 제원이 Table 1과 같은 카고쉽을 대상으로 하였으며, 회두각 유지 제어기는 속도형 퍼지 PID형 오토파일럿을 사용하여 PD형 오토파일럿의 단점을 보완하였다. 그리고 선박이 급격한 변침으로부터 안정성을 확보하기 위해 조타각을 ± 20˚로 제한하였다.

Table 1:

Specification of a cargo ship

여기서, L은 선박의 길이, L_pp는 수선간장, ∇는 재화중량, B는 선박의 폭, Draft는 흘수이다.

7.1 시뮬레이션 조건

Table 2는 시뮬레이션 조건이며 미지의 외란으로 해류, 파도, 바람을 인가하여 실제와 비슷한 환경을 만들었으며 설정된 변침점을 바탕으로 기준 회두각은 약 0˚, 45˚,90˚,20˚,- 51˚이다.

Table 2:

Simulation condition

7.2 시뮬레이션 결과

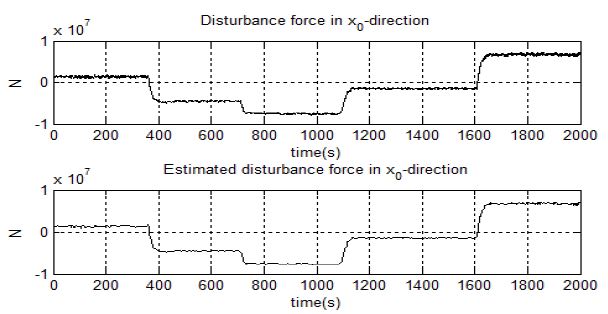
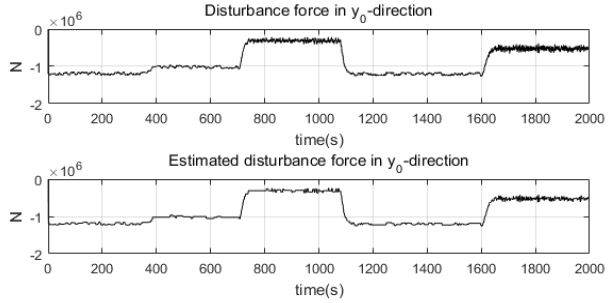
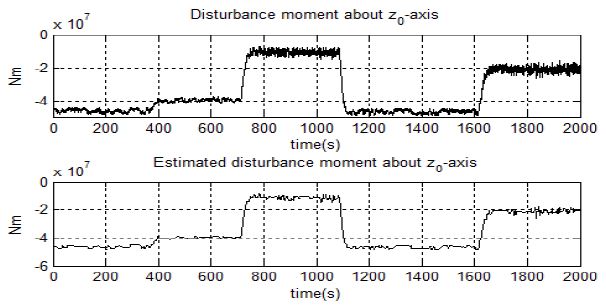
Figure 9 ~ Figure 11은 미지의 외란으로 인해 선박에 추가되는 힘과 모멘트와 이를 퍼지 외란 추정기로 추정하여 비교한 결과이다. 퍼지 외란 추정기가 선박에 추가되는 힘과 모멘트를 정상적으로 추정하는 것을 확인할 수 있으며 미지의 외란 추정값을 피드백 시켜준다면 선박 운동을 방해하는 미지의 외란의 영향을 줄여 줄 것이라 판단할 수 있다.

Figure 9:

Comparison of disturbance forces in x0-direction

Figure 10:

Comparison of disturbance forces in y0-direction

Figure 11:

Comparison of disturbance moments about z0-axis

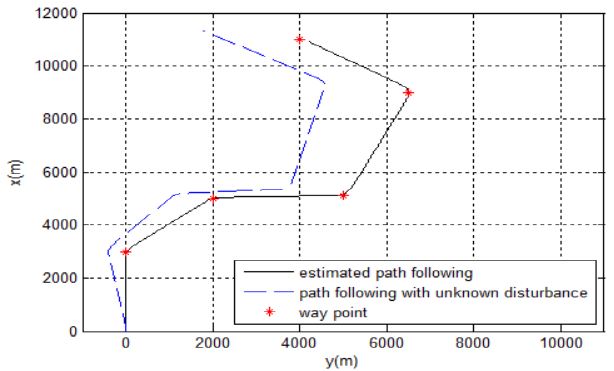
Figure 12는 미지의 외란이 인가된 경우와 이를 퍼지 외란 추정기를 통해 보상시켜준 경우 선박의 위치를 비교한 결과이다. 미지의 외란이 인가된 경우 선박이 정해진 항로를 유지하지 못하고 벗어나지만 미지의 외란으로 인해 선박에 추가되는 힘과 모멘트를 퍼지 외란 추정기로 그 크기를 추정하고 이를 피드백 시켜 보상시켜준 결과 선박이 정해진 항로에서 크게 벗어나지 않고 이동하는 것을 알 수 있다.

Figure 12:

Comparison of path following using and nonusing disturbance estimator

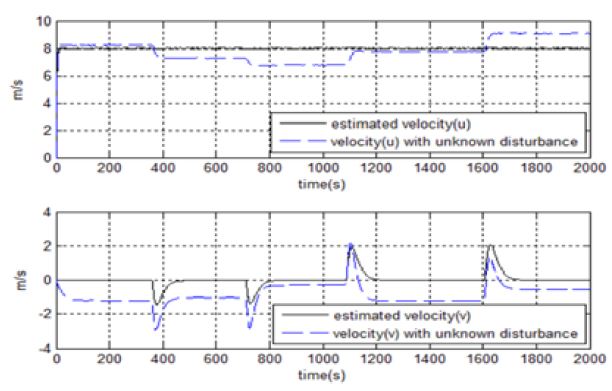
Figure 13은 미지의 외란이 인가된 경우와 이를 퍼지 외란 추정기를 통해 보상시켜준 경우 선박의 속도를 나타내는 시뮬레이션 결과이다. 미지의 외란이 인가된 경우 선박의 전진방향 속도 초기 설정값 8m/s를 유지하지 못하며 횡방향 속도 역시 변침을 제외한 구간에서도 속도가 발생해 항로를 이탈한다. 그러나 미지의 외란으로 인해 발생하는 힘과 모멘트의 크기를 추정하고 이를 피드백 시켜 보상시켜준 결과 선박이 초기 설정값 8m/s를 유지하고 횡방향 속도 역시 변침을 제외한 구간에서 발생하지 않는 것을 알 수 있다.

Figure 13:

Comparison of velocities u, υ using and nonusing disturbance estimator

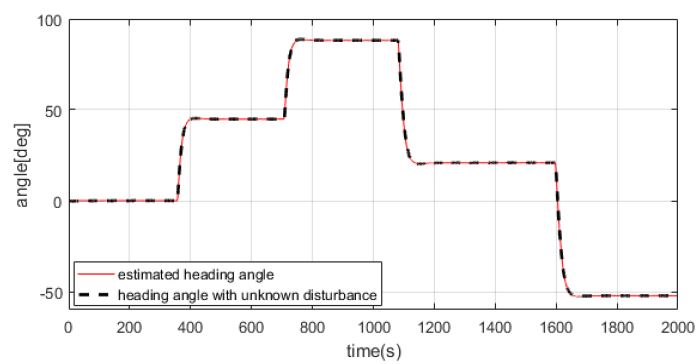
Figure 14는 미지의 외란이 인가된 경우와 이를 퍼지 외란 추정기를 통해 보상시켜준 경우 선박의 회두각을 비교한 결과이다. 미지의 외란이 인가되더라도 기본적으로 오토파일럿에 의해 회두각은 유지가 되는 것을 알 수 있다.

Figure 14:

Comparison of heading angles using and non-using disturbance estimator

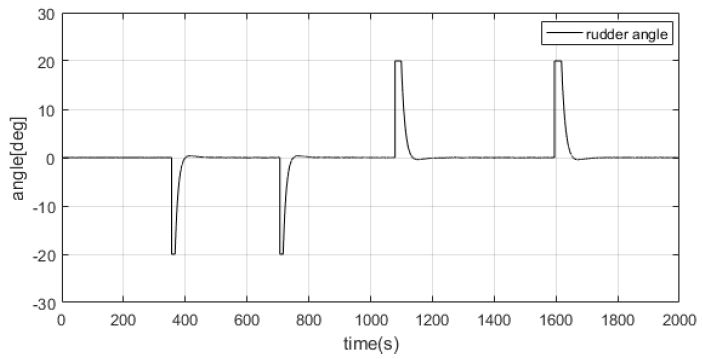
Figure 15는 선박의 조타각을 ± 20[deg]로 제한하여 선박의 안정성을 확보하였다.

Figure 15:

rudder angle

8. 결 론

선박이 운항하는데 에너지 손실을 줄이기 위해 가장 중요한 점이 설정된 항로를 최대한 벗어나지 않으면서 운항하는 것이다. 그러나 변침각이 큰 경우 PD제어기형 오토파일럿은 오버슈트가 발생하고 정착시간이 오래 걸려 항로에서 벗어나게 된다. 또한 비선형성이 강한 경우 한계가 있다. 이와 같은 문제점을 해결하기 위해 속도형 퍼지 PID제어기 오토파일럿을 적용하여 PD제어기형 오토파일럿의 단점을 보완하였다. 그러나 아무리 우수한 성능을 가진 퍼지 PID제어기형 오토파일럿을 사용한다 하더라고 선박 외부에서 미지의 외란이 인가된다면 선박은 정해진 항로를 벗어나게 된다. 이와 같은 문제를 해결하기 위해 본 논문에서는 미지의 외란으로 인해 선박에 추가되는 힘과 모멘트를 퍼지 외란추정기를 이용하여 그 크기를 추정하고 이를 다시 피드백시키는 방법을 제안하였다. 시뮬레이션을 통해 미지의 외란이 인가됨에도 불구하고 선박이 정해진 항로에서 크게 벗어나지 않고 운항할 수 있는 가능성을 확인하였다.

References

• A. E. Sperry, “Directional stability of automatically steered bodies”, Journal of the American Society of Naval Engineers, 42(2), p284, (1992).
• T. I. Fossen, Recent Development in Ship Control Systems Design, London, USA, Sterling Publications Limited, (1999).
• I. H. Kim, A Study on the Design Method of a Nonlinear Fuzzy PID Controller with Variable Parameters, Ph.D. Dissertation, Department of Control and Instrumentation Engineering, Korea Maritime University, Korea, (2004), (in Korean).
• J. H. Kim, Y. S. Ha, and B. K. Lee, “A fuzzy PID controller type autopilot system for route-tracking of ships”, Journal of the Korean Society of Marine Engineering, 30(6), p760-769, (2006), (in Korean).
• B. K. Lee, and J. H. Kim, “A proposal of an LOS guidance system of a ship for path following”, Journal of the Institute of Control Robotics and System, 11(4), p363-368, (2005), (in Korean).
• B. K. Lee, An Optimal Route Decision and LOS Guidance system for Automatic Navigation of Ships, Ph.D. Dissertation, Department of Control and Instrumentation Engineering, Korea Maritime University, Korea, (2005), (in Korean).
• T. I. Fossen, Handbook of Marine Craft Hydrodynamics and Motion Control, Sussex, England, John Willy & Sons Ltd, (2011). [https://doi.org/10.1002/9781119994138]
• T. I. Fossen, Marine Control Systems, Trondheim, Norway, Marine Cybernetics, (2001).
• O. M. Faltinsen, Sea Loads on Ship and Offshore Structures, New York, USA, Cambridge University Press, (1990).
• T. I. Fossen, Guidance and Control of Ocean Vehicles, Sussex, England, John Willy & Sons Ltd, (2011).
• R. M. Iserwood, “Wind resistance of merchant ships”, Journal of the Royal Institution Naval Architects, 115, p327-338, (1972).
• J. H. Kim, J. K. Lim, S. K. Seo, and Y. S. Ha, “Kalman filter based estimation algorithm for uncertainty estimation of LTI system”, Proceedings of the KOSME Fall Conference, p157, (2012), (in Korean).
• S. H. Park, State Estimation and Control of Stochastic System under Unknown Disturbance and Noises, M.S. Dissertation, Department of Control and Instrumentation Engineering, Korea Maritime and Ocean University, Korea, (2016), (in Korean).
• S. K. Seo, State Estimation Algorithm with Fuzzy Estimation Technique for Linear Time Invariant Uncertain Systems, M.S. Dissertation, Department of Control and Instrumentation Engineering, Korea Maritime University, Korea, (2013), (in Korean).