기동 특성을 가진 표적의 상태 추정을 위한 기동 보상 Kalman 필터

1. 서 론

표적 추적은 대상을 인식하고 관측 시스템으로부터 얻은 정보를 사용하여 목표물을 지속적으로 추적하는 것으로 정의된다. 표적 추적의 관건은 대상 표적의 시스템 잡음과 여러 환경적 요소들로 인한 측정 잡음이 누적된 관측된 상태를 실시간으로 보정하여 실제 상태와의 오차를 최소화 하는 것이다. 관측된 상태로부터 신뢰할 수 있는 오차 범위 내에서 표적의 상태를 추정할 수 있는 대표적인 수단으로 표준 Kalman 필터가 널리 사용된다[1]-[6]. 표준 Kalman 필터는 표적이 선형운동을 하고, 운동의 수학적 모델을 정확히 알고 있으며, 표적의 운동에 포함된 시스템 잡음과 관측 잡음이 통계적 평균 0의 백색 가우시안의 특성을 갖는다는 전제 조건 하에 지연 시간 없이 뛰어난 상태 추정 성능을 보인다.

만약 비행 궤도 왜곡 등 기동 특성이 작용하여 표적의 운동이 급격하게 변한다면 초기 설정에 의존하여 연산을 수행하는 표준 Kalman 필터를 사용한 상태 추정에서는 기동 특성에 대한 연산이 이뤄지지 못한다. 따라서 표적의 실제 상태와 표준 Kalman 필터를 사용하여 추정한 상태의 차이인 추정 오차가 증가하게 되어 표적의 상태 추정에 실패하게 된다. 이와 같이 표적의 급격한 상태 변화로 인해 상태 추정에 실패하게 되는 문제점을 해결하기 위해 잡음 공분산 행렬 Q와 R을 추정하는 적응 Kalman 필터[7][8], 표적의 거동을 일정 구간씩 선형화하여 상태를 추정하는 확장 Kalman 필터[9], 비선형 변환을 통해 최소 집합의 시그마 포인트를 얻어 각각에 가중치를 부여한 후 그에 대한 평균을 구하여 상태를 추정하는 분산점 Kalman 필터[10]등이 사용되었다. 언급된 방법들은 비선형 칼만 필터로 매 샘플링마다 선형화 과정을 거치게 되는데, 이 과정에서 계산량이 증가함에 따라 지연시간이 발생하여 표준 칼만 필터에 비해 추정 속도가 느려지게 된다. 따라서 지연 시간 없이 기동 특성이 존재하는 표적에 대한 정확한 상태 추정을 위해선 표준 Kalman 필터와 표적의 기동 특성으로 인해 발생하는 추정 오차를 보상할 수 있는 보상기를 결합하는 것이 타당하다.

본 논문에서는 선형운동을 하는 표적에 기동 특성이 작용할 경우 필터 이노베이션이 증가한다는 점에 착안하여, 필터 이노베이션을 입력으로 표적의 기동 특성을 추정하는 퍼지 기동 추정기[11]-[13]와 표준 Kalman 필터를 결합하여 추정된 기동 특성을 표준 Kalman 필터의 상태 추정 과정에 보상함으로써 추정 성능을 개선하는 기동 보상 Kalman 필터를 제안한다. 제안된 필터의 성능을 검증하기 위해 속력에 대한 기동 특성이 스텝으로 인가되는 경우를 가정하여 시뮬레이션을 수행하고 그 결과를 고찰한다.

2. 기동 표적 모델링

3. 표준 Kalman 필터

표준 Kalman 필터는 재귀 필터로, 직전 샘플링에서 추정한 상태를 토대로 현재 샘플링에서의 상태를 추정한다. 추정 과정은 두 단계로 구분할 수 있는데, 직전 샘플링에서 추정된 표적의 상태를 토대로 예상되는 현재 샘플링에서의 상태를 계산하는 예측 단계와, 예측된 상태와 측정된 상태를 토대로 현재 샘플링에서의 상태를 추정하는 보정 단계로 나뉜다. 표준 Kalman 필터는 이와 같은 과정에 대해 시간 지연 없이 뛰어난 추정 성능을 보인다[1]-[6].

식 (2)와 같은 상태 방정식을 갖는 표적에 대한 표준 Kalman 필터 알고리즘은 식 (4)와 같다.

여기서, (-) 와 (+)는 각각 예측과 추정을 의미하며, K는 표준 Kalman 필터의 이득을 나타낸다. Q는 시스템 잡음 w_k의 공분산 행렬, R은 관측 잡음 υ_k의 공분산 행렬, P는 추적 오류 통계를 나타내는 필터 공분산 행렬이다[3]-[5]. 예측된 상태 $$ {\widehat{x}}_k$$(-) 와 출력 행렬 C를 곱한 $$ {\widehat{z}}_k$$는 예측 측정 값을 나타내며, 측정값과 예측 측정값의 차이인 필터 이노베이션은 e_k로 나타낸다.

표준 Kalman 필터는 입력된 초기 값들을 바탕으로 표적의 상태를 추정하므로 미지의 상태 변화인 기동 특성은 표준 Kalman 필터의 추정 과정에 포함되지 않는다. 따라서 등속운동을 하는 표적의 상태 추정에선 필터 이노베이션의 통계적 평균이 0에 수렴하지만, 기동 특성으로 인해 상태 추정 도중 표적의 속력이 변하게 되면 관측된 상태와 예측된 상태 사이에 오차가 발생하게 되어 필터 이노베이션이 통계적으로 0에 수렴한 상태에서 벗어나게 된다. 알고리즘의 보정 단계에서 예측된 상태에 대해 필터 이득을 통한 보상이 이뤄지지만 필터 이득은 시간이 지남에 따라 급격히 감소하여 0에 근접한 값에 수렴하게 되므로 실제 표적의 상태와 추정된 상태 사이의 차이가 증가하게 되어 상태 추정에 실패하게 된다.

4. 퍼지 기동 추정기

4.1 기본 구조

표준 Kalman 필터를 이용한 상태 추정 과정에서 필터 이노베이션의 통계적 평균이 기동 특성 존재 판단의 기준이 될 수 있으며, 식 (5)와 같은 수식으로 나타낼 수 있다.

$\[ S=\left|\sum _{i=0}^{n-1}\left(e_{k-i}\right)\right|>\eta , i=\mathrm{0,1},\dots ,n \]$

(5)

여기서 e_k는 k번째 샘플링에서 발생하는 필터 이노베이션이며, S는 최신의 k번째 샘플링부터 k - (n - 1)번째 샘플링까지, 임의의 자연수 n개의 연속하는 필터 이노베이션들을 합한 값의 크기다. 필터 이노베이션은 백색 가우시안 잡음의 영향을 받아 특성이 비슷하므로, 선형운동을 하는 표적의 상태 추정 과정에서 n개의 연속하는 필터 이노베이션들의 합의 크기인 S가 0에 수렴하게 되는데, 기동 특성이 존재할 경우 필터 이노베이션의 크기가 전반적으로 증가하므로 S 또한 증가하게 된다. η는 문턱 값으로, S와 비교함으로써 기동 특성의 존재 유무를 판단한다. 조건을 만족할 경우 퍼지 기동 추정기를 통해 기동 특성을 추정하여 다음 샘플링의 예측 단계에 보상한다.

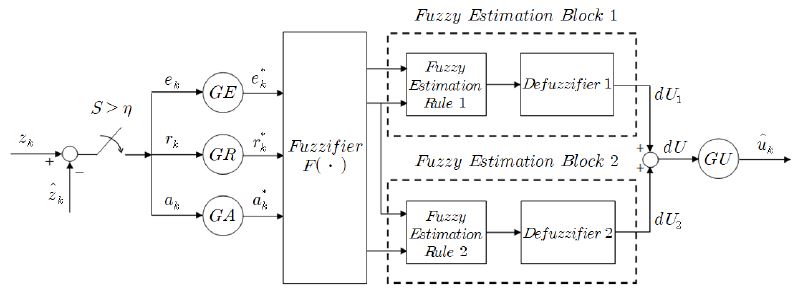
Figure 1은 제안하는 퍼지 기동 추정기의 기능선도를 나타낸 것이다. 추정기의 입력으로 필터 이노베이션 e_k를 이용하여 여러 변수를 생성해 사용한다. 변수들은 식 (6)과 같다[11]-[13].

Figure 1:

Functional diagram of fuzzy maneuver estimator

$\[ \begin{array}{c}{e}_k=z_k-{\widehat{z}}_k, e_k^{*}=GE\times e_k\\ r_k=e_k/T, r_k^{*}=GR\times r_k\\ a_k=\left[r_k-r_{k-1}\right]/T, a_k^{*}=GA\times a_k\\ GE=L/\left|e_k\right|, GR=L/\left|r_k\right|\\ GA=L/\left|a_k\right|, GU=4/GR \\ dU=d{U}_1+d{U}_2, {\widehat{u}}_k=GU\times dU\end{array} \]$

(6)

여기서, T는 샘플링 주기, r_k와 a_k는 각각 이노베이션 e_k를 T로 나눈 것과 e_k의 변화율이다. 입력변수 e_k, r_k, a_k는 각각 입력 스케일 파라미터 GE, GR, GA와 곱해져 e_k^*, r_k^* , a_k^*로 정규화된다. L은 퍼지 기동 추정기의 입력과 출력을 정규화시키기 위한 정규화 파라미터로, 추정기의 설계자가 결정하는 설계 파라미터이다. 정규화된 입력들은 퍼지화기를 통해 퍼지화되어 퍼지 추정 블록 1과 퍼지 추정 블록 2에 입력된 후 퍼지 규칙에 따라 퍼지집합에 소속된다. 이후에 비퍼지화기를 거쳐 각각의 퍼지집합에 따른 출력 값 dU₁, dU₂를 갖게 되는데, dU₁, dU₂을 합한 dU에 출력 스케일 파라미터 GU를 곱하여 기동 특성 추정 값 $$ {\widehat{u}}_k$$를 얻는다. 이때, 매 샘플링 시간마다 GR이 변경됨에 따라 출력 스케일 파라미터 GU 또한 변하여 샘플링마다 새로 추정된 $$ {\widehat{u}}_k$$를 얻을 수 있다. 식 (5)를 만족하지 않을 경우에 $$ {\widehat{u}}_k$$는 0의 값을 갖는다.

4.2 퍼지화 알고리즘

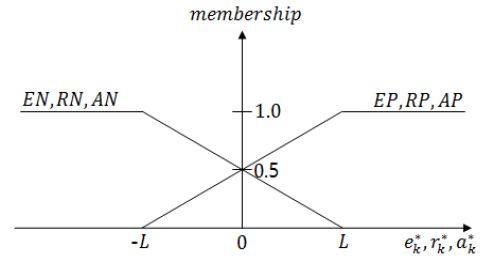
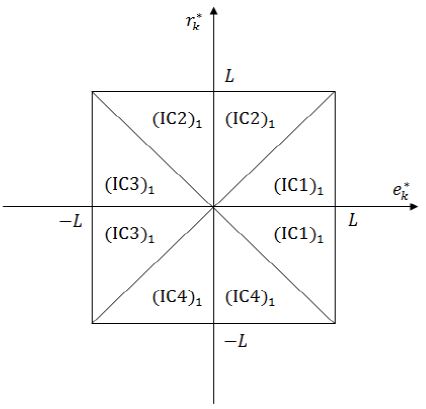
퍼지 기동 추정기의 입력으로 사용되는 정규화된 입력변수 e_k^*, r_k^*, a_k^*의 공간에서 정의되는 소속함수는 Figure 2와 같다[11]. 입력변수 e_k^*의 공간에선 EP(error positive)와 EN(error negative), r_k^*의 공간에선 RP(rate positive)와 RN(rate negative), a_k^*의 공간에선 AP(acc positive)와 AN(acc negative), 각각 두 개의 퍼지 집합이 정의된다.

Figure 2:

Fuzzification for input of fuzzy maneuver estimator

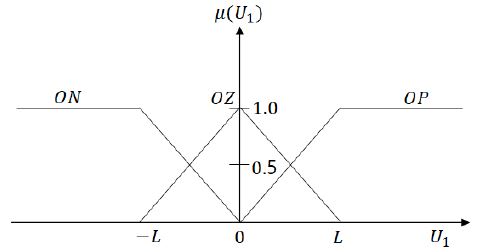
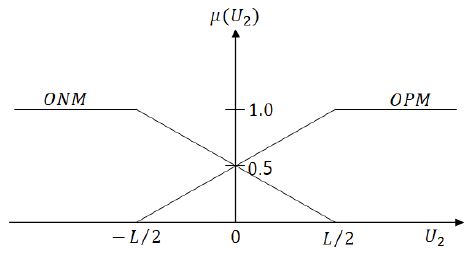
Figure 3, Figure 4는 퍼지 추정 블록 1과 퍼지 추정 블록 2의 출력인 U₁과 U₂의 공간에서 정의되는 소속함수를 나타낸다[11]. U₁의 공간에 대해선 OP(output positive), OZ(output zero), ON(output negative) 세 개의 퍼지집합이, U₂의 공간에 대해선 OPM(output positive middle), ONM(output negative middle) 두 개의 퍼지 집합이 정의된다.

Figure 3:

Fuzzification for output of fuzzy control block 1

Figure 4:

Fuzzification for output of fuzzy control block 2

4.3 퍼지 추정 규칙

퍼지 추정 블록 1과 퍼지 추정 블록 2에 대한 퍼지 추정 규칙은 식 (7), 식 (8) 같이 각각 네 개의 선형적 퍼지규칙으로 이루어져 있으며 이를 통해 각 추정 블록의 출력값 U₁, U₂를 도출해 낸다. 퍼지규칙에서 각 규칙의 전반부를 판단하는 추론논리로는 Zadeh의 AND 논리를 적용하며, 각각의 규칙을 결합하는 논리로는 Lukasiewicz OR 논리를 적용한다[11].

$\[ \begin{array}{c}{\left(R1\right)}_1:IF e_k^{*}=EP \text{and} r_k^{*}=RP, U_1=OP\\ {\left(R2\right)}_1:IF e_k^{*}=EP \text{and} r_k^{*}=RN, U_1=OZ\\ {\left(R3\right)}_1:IF e_k^{*}=EN \text{and} r_k^{*}=RP, U_1=OZ\\ {\left(R4\right)}_1:IF e_k^{*}=EN \text{and} r_k^{*}=RN, U_1=ON\end{array} \]$

(7)

$\[ \begin{array}{c}{\left(R1\right)}_2:IF r_k^{*}=RP \text{and} a_k^{*}=AP, U_2=OPM\\ {\left(R2\right)}_2:IF r_k^{*}=RP \text{and} a_k^{*}=AN, U_2=ONM\\ {\left(R3\right)}_2:IF r_k^{*}=RN \text{and} a_k^{*}=AP, U_2=OPM\\ {\left(R4\right)}_2:IF r_k^{*}=RN \text{and} a_k^{*}=AN, U_2=ONM\end{array} \]$

(8)

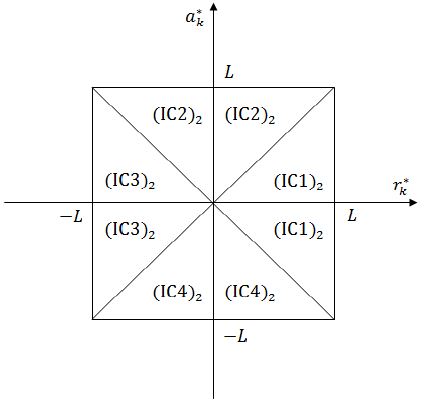
식 (7), 식 (8)과 같은 퍼지 추정 규칙들을 퍼지 추정 블록 1과 퍼지 추정 블록 2에 적용하기 위한 입력공간은 식 (6)과 같이 매 샘플링마다 스케일 파라미터들을 갱신함으로써 퍼지 기동 추정기의 크기가 변하여도 Figure 5, Figure 6과 같이 [-L, L] 의 범위 내에서 정의될 수 있도록 간단하게 분할할 수 있다.

Figure 5:

Possible input partitions of ek* and rk*

Figure 6:

Possible input partitions of rk* and ak*

5. 시뮬레이션

제안된 필터의 성능을 검증하기 위해 임의의 속력으로 선형운동하는 가상의 표적을 대상으로 표준 Kalman 필터와 제안된 기동 보상 Kalman 필터를 사용한 표적 상태 추정 시뮬레이션을 수행하여 추정 성능을 비교, 분석한다.

5.1 등속운동에 대한 표준 Kalman 필터의 성능

대상 표적은 한 축에 대해서만 등속운동 하는 표적이며, 초기 위치 x₁ = 0에서 임의의 속력 100m/s로 등속운동을 시작한다. 이 때, 식 (2)의 운동 방정식에서 확인할 수 있듯이, s_k를 통해 속력이 인가되므로 s₀ = 100m/s이며, x₂의 초기 값은 0이다. 등속운동을 하는 표적이므로 기동 특성은 u_k = 0으로 인가되지 않는다. 샘플링 주기 T는 0.01초로 가정한다. 시뮬레이션에 적용된 시스템 잡음과 관측 잡음의 통계적 특성은 식 (12)와 같이 나타낼 수 있다.

$\[ \begin{array}{c}{w}_k~N\left({\mathrm{0,1}}^2\right)\\ {\upsilon }_k~N\left({\mathrm{0,3}}^2\right)\end{array} \]$

(12)

시스템 잡음 w_k는 평균이 0, 분산이 σ² = 12 , 관측 잡음 υ_k는 평균이 0, 분산이 σ² = 32인 백색 가우시안 잡음이다.

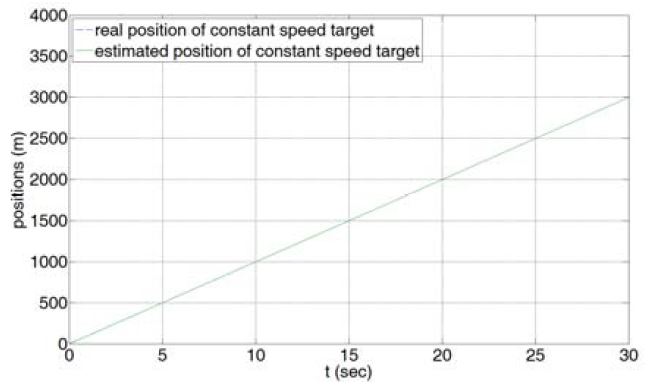
앞에서 설정한 조건에 따라 표준 Kalman 필터를 사용하여 등속운동을 하는 표적의 상태 추정을 할 경우, 시간 t에 따른 표적의 실제 위치와 추정된 위치는 Figure 7와 같다. 표준 Kalman 필터에 의한 상태 추정 오차가 과도상태에선 2m 이내, 정상상태에선 0.03m 이내로 나타나 신뢰할 수 있는 오차범위 내에 있으며 상태 추정이 안정적임을 확인할 수 있다.

Figure 7:

Positions of constant speed target in x direction

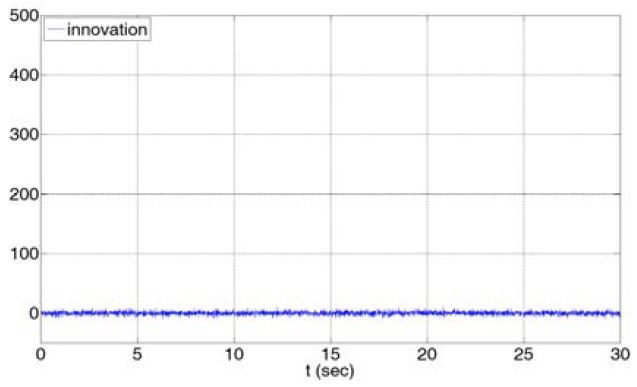
Figure 8은 표준 Kalman 필터를 사용하여 표적의 상태를 추정할 경우에 발생하는 필터 이노베이션을 나타낸다. 상태 추정이 안정적임에 따라 필터 보상 역할을 하는 필터 이노베이션의 통계적 평균이 0으로 수렴하여 나타나는 것을 확인할 수 있다.

Figure 8:

Kalman filter innovation for constant speed target

5.2 기동 특성에 대한 표준 Kalman 필터의 성능

표적의 기동 특성이 존재할 경우 표준 Kalman 필터의 추정 성능을 확인하기 위해 등속운동 하는 표적에 식 (13)과 같이 속력 변화에 대한 임의의 기동 특성을 스텝으로 인가한다.

(13)

실제 표적이 등속운동하기 위해선 지속적으로 동일한 힘이 인가되어야 한다. 만약 기존의 연구들에서 사용된 식 (1)과 같은 상태 방정식에 식 (13)과 같은 기동 특성을 인가한다면 행렬 A에 의해 속력이 매 샘플링마다 계속 증가하게 될 것이다. 하지만 상태 방정식을 식 (2)와 같게 함으로써 지속적으로 속력 변화에 대한 기동 특성을 인가하더라도 표적의 속력이 초기 속력에 기동 특성이 더해진 값으로 일정하게 유지될 수 있다. 따라서 식 (2)와 같은 상태 방정식을 통해 표적을 질점으로 가정하는 표적 추적에서도 운동의 역학적 특성을 고려하여 나타낼 수 있다.

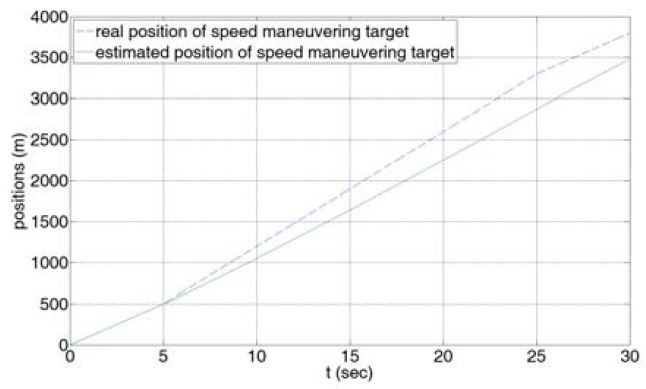
등속운동 하는 표적에 식 (13)과 같은 기동 특성 u_k를 인가할 경우 시간 t에 따른 표적의 실제 위치와 추정된 위치는 Figure 9와 같다. Figure 10에서 볼 수 있듯이 기동 특성이 인가되는 5초에서 25초 사이에 표적의 실제 위치와 추정된 위치의 차이가 점점 증가하여 그 차이가 약 400m까지 이르게 된다. 이는 식 (4)에서 확인할 수 있듯이 표준 Kalman 필터의 상태 추정 과정에선 초기 값에 대한 연산만 이뤄지므로 기동 특성에 대한 계산이 존재하지 않기 때문이다. 기동 특성이 사라진 25초 이후엔 추정된 상태 $$ {\widehat{x}}_k$$(+)를 구하는 과정에서 필터 이득과 필터 이노베이션의 곱을 예측 추정치에 보상함으로써 위치 추정오차가 점차 감소하지만 그 크기가 매우 작아 오차가 지속된다.

Figure 9:

Positions of speed maneuvering target in x direction

Figure 10:

Kalman filter innovation for speed maneuvering target

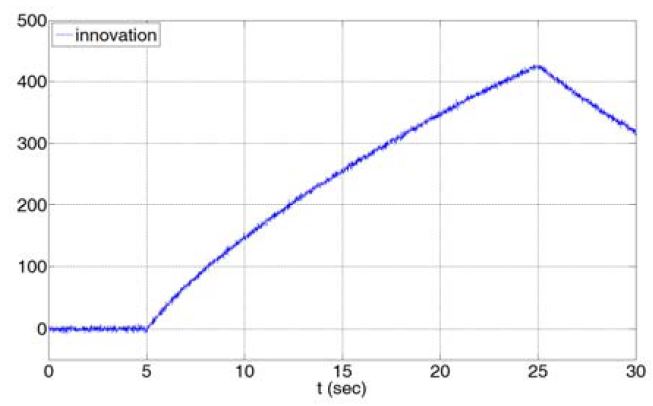
속력 변화에 대한 기동 특성이 인가되기 시작한 5초 이후에 표적의 실제 위치와 추정된 위치의 차이가 점점 증가함에 따라 Figure 10에서 확인할 수 있듯이 필터 이노베이션이 크게 증가하며 통계적 평균이 0인 상태에서 벗어나는 것을 확인할 수 있다. 이는 표준 Kalman 필터가 정상상태에서 표적의 상태를 제대로 추정하지 못하고 발산함을 의미한다.

5.3 제안된 기동 보상 Kalman 필터의 성능

Figure 9와 Figure 10에서 표적에 기동 특성이 존재할 경우 위치 추정 오차가 점점 커지는 등의 문제점을 확인하였다. 이를 해결하기 위해 기동 보상 Kalman 필터를 제안하였으며, 시뮬레이션을 수행하여 제안된 필터의 성능을 확인한다.

제안된 필터는 식 (5)를 기반으로 기동 특성의 존재 유무를 판단한다. 기준을 만족할 경우, 표적 상태 추정 과정에서 발생하는 필터 이노베이션을 기반으로 구한 기동 특성의 추정 값 $$ {\widehat{u}}_k$$를 Kalman 필터 알고리즘의 예측 추정치를 구하는 과정에 보상함으로써 기동 특성에 의한 추정 오차를 보상한다. 퍼지 기동 추정기의 설계 파라미터 L은 1로 가정한다.

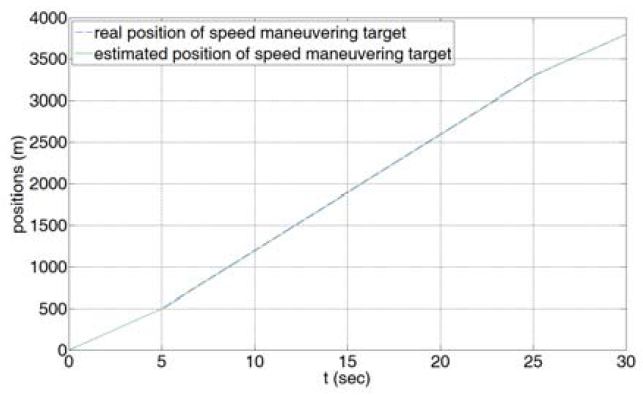
기동 특성이 존재할 경우 표적의 실제 위치와 제안된 기동 보상 Kalman 필터를 통해 추정한 표적의 위치는 Figure 11과 같다. 기동 특성이 존재하는 구간에 최대 10m 의 추정 오차가 존재하지만 표준 Kalman 필터를 사용한 상태 추정과 비교하여 제안된 기동 보상 Kalman 필터는 발산하지 않고 효과적으로 기동 특성에 대응함을 알 수 있다.

Figure 11:

Positions of speed maneuvering target based on compensated Kalman filter in x direction

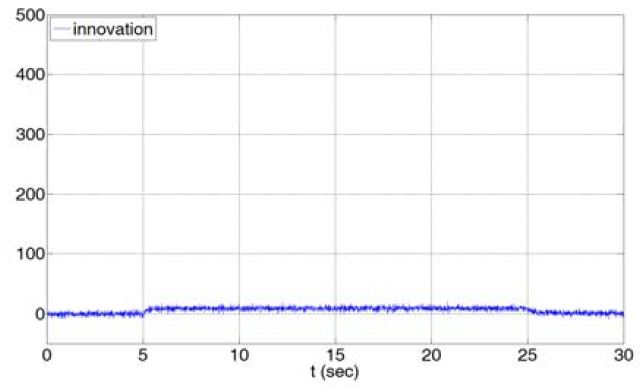
Figure 11에서 볼 수 있듯이 추정 오차가 감소하여 추정된 위치의 정확도가 증가함에 따라 이노베이션 또한 Figure 12에서 나타나는 것과 같이 통계적 평균이 0에 근접하게 수렴한다.

Figure 12:

Compensated Kalman filter innovation for speed maneuvering target

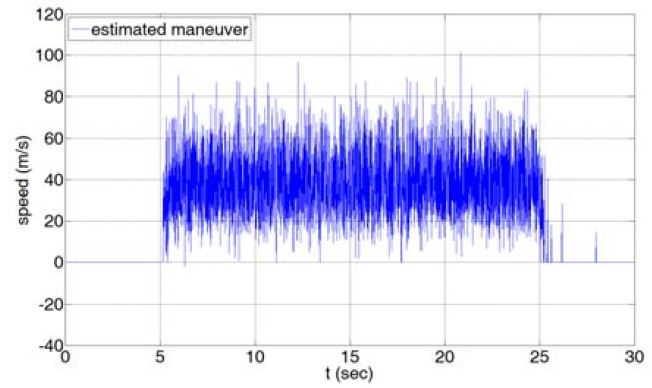
퍼지 기동 추정기를 통해 추정된 $$ {\widehat{u}}_k$$는 Figure 13과 같다. Figure 13에서 확인할 수 있듯이, 추정기는 기동 특성이 인가된 5초 이후, 약 0.2초의 시간 지연 후에 그 값을 추정한다. 표적 상태 추정 과정에서 발생하는 필터 이노베이션의 편차에 따라 기동 특성 추정 값의 변동이 존재하지만 기동 특성이 입력된 5초에서 25초 사이에 추정된 $$ {\widehat{u}}_k$$는 통계적 평균이 40에 수렴하는 것을 확인할 수 있으며, 이는 속력에 대한 기동 특성의 크기에 해당한다. 이때 발생하는 0.2초의 시간 지연은 퍼지 기동 추정기가 식 (5)와 같은 필터 이노베이션을 이용해 기동 특성의 존재 유무를 판단하는 과정에서 발생하며, 시간 지연동안 기동 특성에 의한 표적의 운동을 보상하지 못하게 되어 작은 오차가 존재하게 된다.

Figure 13:

Estimated target maneuver by fuzzy maneuver estimation algorithm

6. 결 론

표준 Kalman 필터는 동적 특성이 변하지 않는 선형운동을 하는 표적의 상태 추정에 적합한 이론이다. 한편, 본 논문에서 살펴보았듯이, 속력이 급격하게 변하는 등의 요인이 존재 할 경우 표준 Kalman 필터를 사용한 표적의 상태추정에 큰 어려움이 따른다.

본 논문에서는 퍼지 기동 추정기와 표준 Kalman 필터를 결합하여 기동 특성 추정값 $$ {\widehat{u}}_k$$를 표준 Kalman 필터의 상태 추정 과정에 보상함으로써 추정된 상태를 보정할 수 있는 기동 특성 보상 Kalman 필터를 제안하였다. 기동 특성을 갖는 표적에 대해 표준 Kalman 필터와 제안된 필터를 사용한 시뮬레이션을 수행한 결과, 표준 Kalman 필터의 상태 추정 성능의 한계를 확인하였고, 제안된 필터를 통해 안정적 추정이 가능함을 확인하였다. 또한 제안된 필터 사용하여 상태를 추정할 경우 존재하는 작은 오차는 기동 특성 발생 유무를 판단해야 하는 지연시간으로 인해 퍼지 기동 추정기가 기동 특성의 발생에 즉각적인 반응을 하지 못함으로 인해 야기되는 결과임을 확인할 수 있었다.

References

• A. E. Gelb, et al. , Applied Optimal Estimation, MIT Press, Cambridge, (1974).
• M. S. Grewal, and A. P. Andrews, Kalman Filtering Theory and Practice, Prentice Hall, New Jersey, (1993).
• R. A. Singer, and R. Sea, “Increasing the computational efficiency of discrete Kalman filters”, IEEE Transactions on Automatic Control, 16(3), p254-257, (1971). [https://doi.org/10.1109/tac.1971.1099707]
• R. A. Singer, and K. W. Behnke, “Real-time tracking filter evaluation and selection for tactical applications”, IEEE Transactions on Aerospace and Electronic Systems, AES-7(1), p100-110, (1971). [https://doi.org/10.1109/taes.1971.310257]
• R. A. Singer, “Estimating optimal tracking filter performance for manned maneuvering targets”, IEEE Transactions on Aerospace and Electronic Systems, AES-6(4), p473-483, (1970). [https://doi.org/10.1109/taes.1970.310128]
• Y. T. Chan, A. G. C. Hu, and B. Plant, “A Kalman filter based tracking scheme with input estimation”, IEEE Transactions on Aerospace and Electronic Systems, AES-15(2), p237-244, (1979). [https://doi.org/10.1109/taes.1979.308710]
• R. Mehra, “On the identification of variances and adaptive Kalman filtering”, IEEE Transactions on Automatic Control, 15(2), p175-184, (1970). [https://doi.org/10.1109/tac.1970.1099422]
• R. J. McAulay, and E. Denlinger, “A decision-directed adaptive tracker”, IEEE Transaction on Aerospace and Electronic Systems, AES-9(2), p229-236, (1973). [https://doi.org/10.1109/taes.1973.309772]
• S. J. Julier, J. K. Uhlmann, and H. F. Durrant-Whyte, “A new method for the nonlinear transformation of means and covariances in filters and estimators”, IEEE Transactions on Automatic Control, 45(3), p477-482, (2000). [https://doi.org/10.1109/9.847726]
• S. J. Julier, and J. K. Uhlmann, “Unscented filtering and nonlinear estimation”, Proceedings of the IEEE, 92(3), p401-422, (2004). [https://doi.org/10.1109/jproc.2003.823141]
• J. H. Kim, “A suggestion of nonlinear fuzzy PID controller to improve transient response of nonlinear or uncertain systems”, Journal of Korean Institute of Intelligent Systems, 5(4), p87-100, (1995).
• B. K. Lee, J. H. Kim, and I. H. Kim, “A study on the performance improvement of a nonlinear fuzzy PID controller”, Journal of the Korean Society of Marine Engineers, 28(2), p136-144, (2004), (in Korean).
• S. K. Seo, State Estimation Algorithm with Fuzzy Estimation Technique for Linear Time Invariant Uncertain Systems, M.S Dissertation, Department of Control and Instrumentation Engineering, Korea Maritime University, Korea, (2013).
• H. S. Son, J. B. Park, and Y. H. Joo, “Non-linear maneuvering target tracking method using PIP”, Journal of Korean Institute of Intelligent Systems, 17(1), p136-142, (2007), (in Korean). [https://doi.org/10.5391/jkiis.2007.17.1.136]
• H. M. Herab, and H. Khaloozadeh, “Extended input estimation method for tracking non-linear manoeuvring targets with multiplicative noises”, IET Radar, Sonar & Navigation, 10(9), p1683-1690, (2016).