미지의 외란 추정을 이용한 선박의 항로 추종 개선
Copyright © The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
일반적으로 선박은 6자유도 운동방정식으로 구성된다. 그러나 선박이 운항을 하는데 있어서 선박이 평면운동을 한다고 가정해도 무방하기 때문에 X축으로의 운동(Surge), Y축으로의 운동(Sway), Z축으로의 회전(Yaw)으로 이루어진 3자 유도 운동으로 간략화시킬 수 있다. 이때 선박의 운동은 이동운동에 대한 방정식과 회전운동에 대한 방정식의 결합으로 이루어진다. 선박 운항중에 선박 외부에서 미지의 외란으로 해류나 파도가 인가된다면 선박은 PD제어기에 의해 회두각은 유지할 수 있으나 추가되는 힘과 모멘트로 인해 항로에서 벗어나게 된다. 본 논문에서는 선박 외부에서 인가되는 미지의 외란을 보상시켜 주기 위한 Kalman 필터 기반의 퍼지 외란 추정기를 설계하고 이때 추정된 미지의 외란을 피드백시켜 보상함으로써 미지의 외란을 상쇄시켜 주는 제어시스템을 제안한다. 또한 이를 검증하기 위해서 시뮬레이션을 수행한 뒤 그 결과를 기반으로 제안된 방법의 타당성을 검증하고자 한다.
Abstract
In general, a ship motion is described by six degree of freedom equations of motion. However, if the ship follows a course, its motion is assumed to be a plane motion, such as a three degrees of freedom motion, composed of a motion in x-axis, motion in y-axis and rotational motion about z-axis. The ship's motion is modeled by the combination of a speed equation and steering equation. Although an unknown disturbance is affecting a ship, the ship will be able to keep its heading angle properly, but it will deviate from the designated route. In this research, a Kalman filter based on the fuzzy disturbance estimator is designed for compensating unknown disturbance applied from outside of the ship. And the control system that compensates the estimated unknown disturbances using feedback is suggested. To verify the effectiveness of the proposed method, several simulations were performed, and the validity of the method was verified by analyzing the simulation results.
Keywords:
Fuzzy disturbance estimator, Unknown disturbance, Heading angle, Kalman filter키워드:
퍼지 외란 추정기, 미지의 외란, 회두각 유지, 칼만 필터1. 서 론
선박 운항에 있어서 가장중요하게 고려해야 할 사항은 항해 중 발생할 수 있는 침몰 또는 충돌 등에 의한 위험으로부터 선박의 안전성을 확보하고 정해진 항로를 정확하게 추종하도록 하는 것이다. 정확한 항로 추종은 최단시간에 목적지에 도착하는 것이며 또한 운항 중 발생하는 추진 에너지의 손실을 최소화시키는 것이다. 선박 자동화의 목적 또한 선박의 불안정성을 제거하고 선박이 운항하는데 있어서 경제성을 높이는데 있다. 선박운항 자동화를 위해서는 첫 번째, 항로를 결정할 수 있는 항로 결정 알고리즘이 필요하고 두 번째, 결정된 항로를 선박이 제대로 추종할 수 있도록 하는 가이던스 시스템, 마지막으로 가이던스 시스템의 명령에 따라 선박을 제어하는 오토파일럿 시스템이 필요하다[1][2]. 선박이 대형화되고 통항량이 증가함에 따라 고도의 선박 조종 능력이 요구되고 있다. 그러나 선박사고의 원인으로 항해사의 근무태만, 실수 등이 증가함에 따라 자동으로 선박을 운항할 수 있도록 유도하는 가이던스 시스템의 연구 개발의 필요성이 증가하고 있다[3][4]. 지금까지 선박이 정해진 항로를 정확히 추종할 수 있도록 유도하는 작업은 항해사들의 경험과 지식을 통해 이루어져 왔으며, 선박을 제어하는 오토파일럿 시스템으로는 대부분 PD 제어기가 사용되어 왔고 또한 퍼지 PID 제어기를 사용한 연구도 진행되어 왔다[5][6]. 그러나 선박의 외부에서 해류, 바람, 파도와 같은 미지의 외란이 인가된다면, 오토파일럿을 통한 회두각은 유지 할 수 있지만 선박에 추가되는 힘과 모멘트로 인해 항로에서 벗어나게 된다. 본 논문에서는 선박 외부에서 인가되는 미지의 외란으로 인해 발생되는 항로 이탈을 방지하기 위해 Kalman 필터기반의 퍼지 외란 추정기를 설계하고 추정된 미지의 외란을 피드백시켜 보상시켜 주는 제어시스템을 제안한다. 제안된 전체 제어 시스템의 성능을 확인하기 위하여 다양한 변침점을 통해 항로를 설정하여 시뮬레이션을 실시하고 시뮬레이션 결과의 분석을 통해 제안된 방법의 성능과 유효성을 검증한다.
2. 제어시스템 구성방법
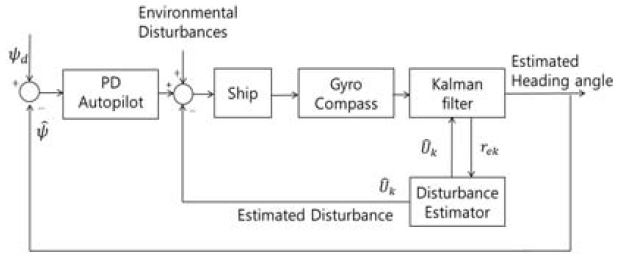
본 논문에서 제안하는 선박 제어를 위한 선박의 제어시스템 구성 개념은 Figure 1과 같다.
선박이 정해진 항로를 운항 하는데 있어서 변침점이 변할 때마다 기준 회두각을 입력받게 된다. 이때 기준 회두각을 유지할 수 있도록 PD형 오토파일럿 제어기를 기본으로 사용하며 조타각 δ는 식 (1)로 구성된다.
| (1) |
여기서, Kp, Kd는 PD제어기의 이득이며 ψd는 기준 회두각을 의미하고 ψ,r은 실제 선박에서 측정된 회두각과 회두각 속도를 의미한다. 식 (1)에서 계산된 조타각이 선박모델의 입력으로 들어감으로써 선박이 회전운동이 발생된다. 선박 운항중에 미지의 외란이 인가되든 인가되지 않든 선박은 PD형 오토파일럿으로 인해 기준 회두각은 유지 할 수 있지만 선박에 추가적인 힘과 모멘트가 인가되기 때문에 정해진 항로에서 벗어나게 된다. 이와 같은 문제를 해결하기 위해서 Kalman 필터기반의 퍼지 외란 추정기를 설계하여 미지의 외란 크기를 추정하고 추정된 미지의 외란을 다시 피드백 시켜서 외란의 영향을 감소시켜 주는 제어시스템 구성방법이 Figure 1이다. 제안된 방법을 적용한다면 선박은 정해진 회두각 유지를 통해 항로를 크게 벗어나지 않고 추종할 수 있다. 여기서 rek는 Kalman 필터의 이노베이션을 의미하고 은 미지의 외란 추정값으로서 이들에 대한 정의와 설명 및 추정방법은 5장에서 상세히 설명한다.
3. 선박 모델
선박의 운동방정식은 6자유도 운동방정식으로 구성이 되어 있고 이를 식으로 나타내면 식 (2)와 같다.
| (2) |
여기서, M은 강체 동역학적 관성행렬, C는 강체 동역학적 Coriolis 행렬, D는 감쇠행렬, τ는 선박이 운항하는데 필요한 추력과 타력을 포함한 힘과 모멘트를 의미하며 τdisturbance는 선박이 운항할 때 외란으로 작용하는 파도, 바람, 해류 등에 의한 힘과 모멘트를 의미한다. 본 논문에서 외란으로 파도와 해류를 적용한다.
3.1 3자유도 선박모델
카고쉽, 오일탱커, 컨테이너선 등과 같이 해수면을 운항하는 선박은 아래의 4가지 조건을 가정한다면 3차원 비선형 선박모델 식 (3)을 유도할 수 있다[7].
- (1) 선박운동은 전진방향 이동운동과 조종운동으로 분리 가능하다.
- (2) 선박의 heave, roll, pitch운동성분의 영향을 무시할 수 있다.
- (3) 선체 고정좌표계의 원점이 선체 중심선에 위치한다.
- (4) 선박은 좌우 대칭이다.
| (3) |
여기서, m은 선체의 질량, ,,은 선가속도 및 각가속도, Iz는 z축에 대한 회전 관성모멘트, xG는 무게중심의 x좌표, X, Y, N은 외력과 모멘트를 의미한다. 그리고 본 논문에서 회두각 유지 제어기로서 선형제어기인 PD제어기를 사용하였기 때문에 3차원 비선형 선박모델을 선형화 시킬 필요가 있다.
3.2 선형화된 선박 운동에 대한 3자유도 상태방정식의 유도
전진방향 속도모델 방정식은 식 (5)로 정의할 수 있다[7].
| (5) |
여기서, t는 스러스트 감소계수, T는 선박이 전진방향 속력을 발생시키는 프로펠러 추력을 의미한다. Tloss는 선박에 추가되는 저항력으로서 [7]에 상세히 설명되어있다. 항력과 프로펠러 추력은 선박운항이 정상상태에 도달할 경우에는 Tloss보다 많은 영향을 받기 때문에 Tloss는 0으로 가정할 수 있다. 이로 인해 식 (5)를 선형화 시키면 식 (6)을 얻을 수 있다.
| (6) |
이와 같은 전진방향 속도 모델을 상태방정식으로 만들면 식 (7)과 같다.
| (7) |
여기서, 라 정의한다.
선박의 선형화된 조종운동 모델은 전진방향 속도가 일정하고, 횡방향속도, 회두각속도가 아주 작다는 가정에서 구할 수 있다. 결국 선박의 전체 속도는 가 되며 조종운동모델은 횡방향속도 υ, 회두각속도 r, 회두각 ψ, 제어입력 조타각 δ의 함수로 표현된다. 선박의 선형 조종운동 방정식은 식 (8)와 같고 유체동역학적 힘과 모멘트는 식 (9)과 같다[7]-[9].
| (8) |
| (9) |
여기서, , 은 유체운동으로 인한 부가질량과 모멘트이고 Yυ, Yδ, Nr, Nδ은 유체력 미계수이다. 식 (8), 식 (9)을 벡터모델로 표현하면 식 (10)과 같다.
| (10) |
여기서, v = [υ,r]T 은 상태벡터, δR은 조타각, M, N(u), b는 식 (11)와 같다.
| (11) |
조종운동방정식의 벡터모델을 상태벡터 xs = [υ,r]T와 δR = δ로 정의하면 식 (12)과 같은 상태방정식을 구할 수 있으며 As, Bs의 행렬의 각각의 요소들은 [7]에 상세히 기술되어 있다.
| (12) |
여기서, As, Bs는 식 (13)와 같다.
| (13) |
4. 해류와 파도의 영향을 받는 선박모델 방정식
4.1 해류가 선박에 미치는 영향
4.2 파도모델의 생성
파도모델을 생성하기 위한 상태공간 방정식은 PM 스펙트럼을 이용해서 만들 수 있기 때문에 PM스펙트럼에 대해 설명한다. PM 스펙트럼의 밀도 함수 S(ω) 는 식 (19)과 같이 이루어진다[11].
| (19) |
여기서, J, K는 식 (20)로 정의된다.
| (20) |
여기서, g는 중력상수를 의미하며 V는 바람의 속도를 의미한다. 그리고 바람의 속도를 통해 파도의 높이 Hs와 파도의 주파수 ω0는 식 (21)로 정의한다[12].
| (21) |
S(ω)를 상태공간 방정식으로 표현하기 위한 수단으로 선형근사 시킨 파워 스펙트럼 밀도 함수 Pyy(ω)는 w(s)가 입력일 때의 출력 y(s)로부터 만들어지며 y(s)는 식 (22)으로 이루어진다.
| (22) |
여기서, h(s) 는 전달함수를 의미하고, w(s) 는 평균이 0인 정규화된 백색 가우시안 잡음을 의미한다. 따라서 파워스펙트럼 밀도 함수 Pyy(ω)는 식 (23)와 같다.
| (23) |
전달함수 h(s) 는 식 (24)와 같이 2차 모델로 가정한다.
| (24) |
전달함수의 이득 Kw는 2λω0σw로 구성되며 여기서 σw는 파도의 밀도, λ는 댐핑 계수, ω0는 파도의 주파수를 의미한다. σw를 구하기 위해서 식 (24)의 전달함수를 주파수 영역으로 변환하면 식 (25)과 같다.
| (25) |
파워 스펙트럼 밀도 Pyy(ω) 의 최대값은 ω = ω0일 경우에 얻을 수 있으며 이를 통해 σw를 얻을 수 있다. 이를 식 (26)과 같이 표현할 수 있다.
| (26) |
식 (26)에서 구한 σw을 바탕으로 식 (24)로 부터 파도의 상태공간 방정식을 만들면 식 (27)과 같다[12].
| (27) |
여기서, w1는 평균이 0이고 분산이 1인 백색 가우시안 잡음을 의미한다. 한편 운항중인 선박의 회두각이 변함에 따라서 실제로 선박에 인가되는 주파수가 변하게 되는데 이를 나타내면 식 (28)와 같다.
| (28) |
여기서, ωe는 실제 선박에 인가되는 주파수, U는 선박의 전진방향 속도, α는 회두각과 파도의 방향 사이의 각도를 의미하며 4.3절에서 ω0대신에 실제 선박에 인가되는 파도의 주파수 ωe를 사용하여 선박의 상태방정식에 반영한다.
4.3 해류 파도를 상태 방정식으로 반영
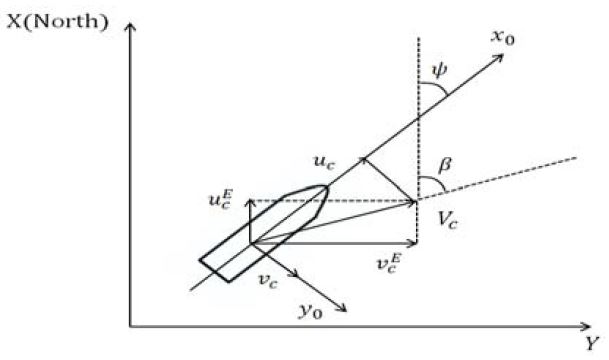
식 (14)의 상태 벡터 x = [u,υ,r]T이다. 그리고 선박 이동좌표계 기준에서 파도의 속도는 식 (18)와 같이 표현된다. 따라서 선박과 파도의 속도를 결합하면 상태 벡터는 [u -Vccos(β - ψ),υ -Vcsin(β - ψ),r]T 로 정의할 수 있고 파도의 진동운동 ψH 는 회두각의 진동으로 표현 가능하기 때문에 [u -Vccos(β - ψ - ψH),υ -Vcsin(β - ψ - ψH),r]T로 해류와 파도가 반영된 상태 벡터가 정의 된다. 따라서 식 (29)과 같은 상태 방정식이 만들어 진다.
| (29) |
여기서, 상태 벡터 x = [u,υ,r]T 로 정의하기 위해 외란(해류, 파도)에 해당하는 값들을 분리해서 표현하면 최종적으로 식 (30)과 같은 상태 방정식이 만들어 진다.
| (30) |
4.4 해류와 파도의 영향이 반영된 선박의 선형 이산확률 상태 공간 방정식
식 (31)는 선박에 외란으로 해류와 파도의 영향이 인가되고 확률적 특성이 변하지 않는 시스템 잡음이 포함된 선형 이산 확률 상태 방정식을 나타낸다[12].
| (31) |
여기서, A,B,Uk-1를 zero-order hold기법으로 이산화 시킨 결과를 A′,B′,Uk-1′이라 정의한다. 상태 벡터 xk = [u,υ,r]T이며 uk = [T,δ]T, wk는 시스템 잡음으로 평균 0의 백색 가우시안 잡음이다. Uk-1′은 미지의 외란으로 실제로는 어떻게 인가되는지 모르는 항이며 선박의 surge, sway yaw성분에 직접적으로 영향을 미쳐 선박의 운동을 방해하는 요소로 작용한다. 식 (31)는 외란의 영향이 반영된 실제 선박의 운동모델로서 본 논문의 시뮬레이션에 사용된다. 한편, 본 논문에서 선박은 평면 운동을 한다고 가정했기 때문에 X, Y방향으로의 운동과 Z축으로의 회전 운동을 하게 된다. 따라서 선박의 위치와 회두각은 선박의 속도를 이용하여 Z축으로의 회전에 해당하는 변환행렬을 곱해준다. 이때 변환 행렬은 식 (32)의 C1과 같다.
선박의 이동경로와 회두각을 출력하는 선박의 출력 방정식은 식 (33)과 같다.
| (32) |
여기서, C1을 zero-order hold기법으로 이산화 시킨 결과를 C1′이라 정의한다. dk1는 Gps, Gyro Compass로부터 선박의 위치와 회두각을 전달받을 때 발생하는 측정 잡음으로 평균이 0인 백색 가우시안 잡음이라 가정한다. 그리고 이노베이션 프로세스를 입력으로 미지의 외란의 크기를 추정하기 위해 사용되는 출력 zk는 선박의 속도와 각속도로 식 (34)와 같고 dk2는 측정 잡음으로 평균이 0인 백색 가우시안 잡음이다.
| (33) |
5. 퍼지 외란 추정기가 결합된 Kalman 필터 기반의 상태추정 알고리즘
선형 시불변 확률 이산시간 시스템에서 Kalman 필터 알고리즘은 시스템의 상태를 잘 추정한다. 그러나 시스템 외부에서 미지의 외란이 인가되는 경우 Kalman 필터는 상태 추정에 실패한다. 이를 보정하기 위해서 불확실성으로 인해 DC성분을 가지고 변하는 이노베이션 프로세스의 특성을 이용하여 미지의 외란의 크기를 추정하는 퍼지 외란 추정기법을 적용한다[13][14].
5.1 불확실성 존재 판단 방법
만약 미지의 외란의 영향으로 인해 이노베이션 프로세스의 확률적 평균이 0근처에서 벗어난다고 가정하고 매 샘플링 시간마다 발생하게 되는 이노베이션 프로세스 값을 제곱하여 특정한 수의 샘플링 구간동안 더한다면 크게 변동되지 않는 값 식 (34)를 얻을 수 있다[14].
| (34) |
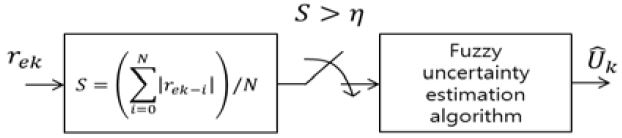
여기서, rek는 샘플링 시간 k에서 발생하는 이노베이션 프로세스이고 S는 윈도우 내에서 계속 축적되는 (N + 1)개의 이노베이션 프로세스 제곱의 합이고, N은 축적하고자하는 데이터 개수의 범위를 정해주는 윈도우이다. 식 (34)에서 계산된 S값을 바탕으로 불확실성의 존재 여부를 판단하는 것은 특정 크기의 문턱값과 비교함으로써 알 수 있다. 이를 나타낸 것이 Figure 3이다.
여기서, η는 문턱값이며 반복적으로 구한 S값을 토대로 설계자가 직접 결정하는 것이며, S > η조건을 만족하는 경우 시스템에 불확실성이 존재하거나 불확실성 입력이 인가되는 경우라고 판단한다.
5.2 퍼지 불확실성 추정 알고리즘
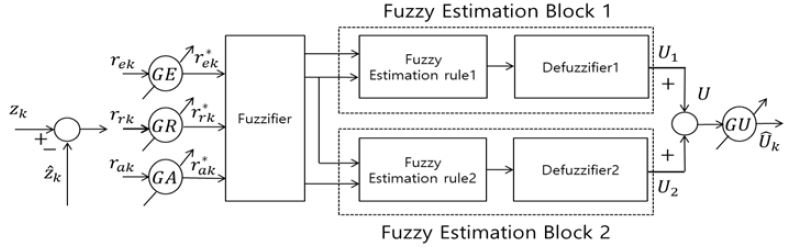
5.1절에서 제안한 방법을 통해 불확실성 존재 여부가 판단된다면 이를 추정할 수 있는 방법이 Figure 4와 같다[15]. Kalman 필터 이노베이션 프로세스를 입력으로 사용하여 퍼지 제어규칙과 비퍼지화기를 포함하는 두 개의 퍼지 추정블록으로 구성된다. 퍼지규칙에 활용할 퍼지 변수들은 식 (35)과 같다.
| (35) |
여기서, zk는 매 샘플링 시간에서의 측정값, 은 예측값이고, T는 샘플링 시간, rrk는 이노베이션rek를 샘플링 시간으로 나눈 값, rak는 이노베이션rek의 샘플링 시간에 따른 변화율이다. GE,GR,GA는 각각 rek, rrk, rak의 크기를 정규화 시키는 입력 스케일 파라미터로서 Figure 3의 S > η조건을 만족시켜 불확실성이 존재할 경우에는 이노베이션의 정상상태 값이 확률적으로 0이 아니기 때문에 유한한 값을 갖는다. GU는 퍼지 출력 U를 위한 스케일 파라미터, L은 입력과 출력을 정규화 시키는 정규화 파라미터이며 이 값들은 설계자가 직접 결정한다. 퍼지 불확실성 추정 알고리즘의 입력으로 들어가는 정규화된 rek*, rrk*, rak*를 퍼지집합으로 퍼지화 시키고 불확실성 추정 블록 1과 2를 통해 퍼지 출력 U1, U2가 생성된다. 퍼지 불확실성 추정 알고리즘에서 사용된 비퍼지화 알고리즘은 무게중심 평균법을 사용하였고, 비퍼지화를 통해 생성된 출력 U1, U2를 합한 후 출력 스케일 파라미터 GU를 곱하여 최종출력으로 미지의 외란 추정값 를 구하면 식 (36)과 같다.
| (36) |
여기서, Ki, Kp, Kd는 식 (37)과 같다.
| (37) |
5.3 Kalman 필터 기반의 상태 추정 알고리즘
불확실성의 크기는 식 (36)에 의해서 로 추정된다. 이를 Kalman 필터 알고리즘에 부가되는 외란으로 피드백 시켜 필터 추정치를 보상시켜 준다면 실제의 상태를 신뢰 할 수 있게 추정할 수 있는 추정 알고리즘을 구성할 수 있다. 식 (38)는 기존의 Kalman 필터 알고리즘에 추정된 미지의 외란이 다음 샘플링 시간에서 입력으로 들어가는 상태 추정 알고리즘을 나타낸다[15].
| (38) |
여기서, 는 k시간에서 필터추정치, (-) 는 예측 추정치, (-) 는 예측 공분산, Kk는 Kalman이득을 나타낸다. 따라서 5장에서 설명한 퍼지 외란 추정기가 결합된 Kalman 필터 기반 상태 추정 알고리즘을 이용하여 를 추정한 뒤 식 (31)의 미지의 외란이 인가되는 부분에 피드백 시켜 상쇄시켜 준다면 미지의 외란의 영향을 제거시켜 줄 수 있는 효과를 가진다.
6. 시뮬레이션
시뮬레이션을 수행하기 위한 선박모델로는 카고쉽을 대상으로 하였으며 카고쉽의 제원은 Table 1과 같다.
여기서, L은 선박의 길이, Lpp는 수선간장, ∇는 재화중량, B는 선박의 폭이다. 그리고 회두각 유지 제어기는 식 (1)과 같은 PD제어기를 사용하였고 Kp는1.5, Kd는 70으로 최적설정하였다.
6.1 시뮬레이션 조건
Table 2와 Table 3은 시뮬레이션 조건과 미지의 외란으로 작용하는 조류와 파도의 조건을 나타낸다. 시뮬레이션은 미지의 외란이 인가된 경우와 미지의 외란이 인가되지 않은 경우를 비교하고, 미지의 외란이 인가된 경우와 미지의 외란을 퍼지 외란 추정기를 통해 보상시켜 준 경우를 비교한 2가지 상황으로 수행되었다.
6.2 미지의 외란이 인가된 경우와 인가되지 않은 경우의 비교
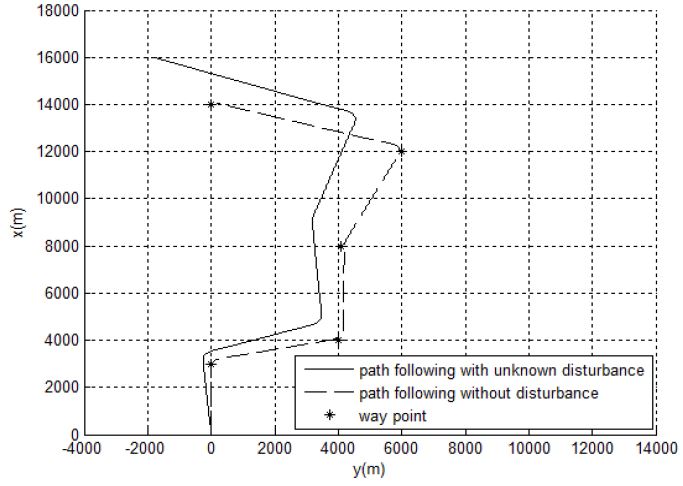
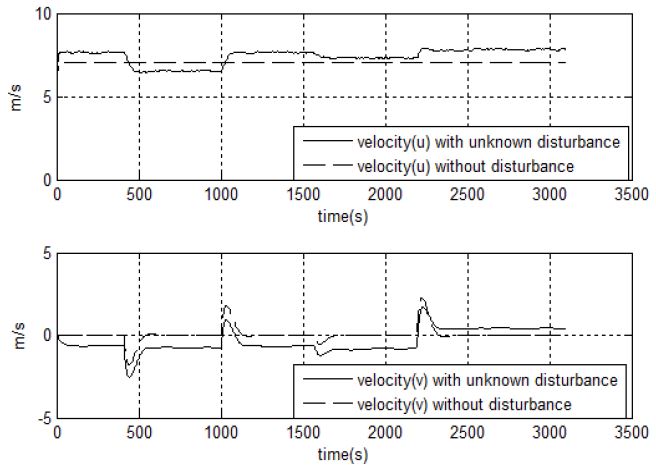
Figure 5는 미지의 외란이 인가된 경우와 미지의 외란이 인가되지 않은 경우 선박의 이동경로를 나타낸 시뮬레이션으로, 미지의 외란이 인가된 경우 선박이 정해진 항로를 점점 벗어나는 것을 알 수 있다. Figure 6은 선박의 속도를 비교한 시뮬레이션으로, 미지의 외란이 인가된 경우 선박의 전진방향 속도가 초기 설정값 7m/s를 유지하지 못하는 것을 알 수 있고 횡방향 속도 역시 미지의 외란의 영향으로 인해 변침을 제외한 구간에서도 횡방향 속도 성분이 생기는 것을 알 수 있다.
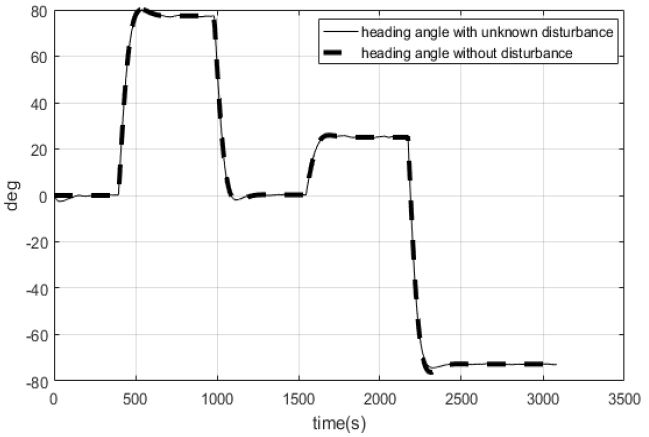
Figure 7은 회두각을 비교한 시뮬레이션으로 미지의 외란의 인가 여부에 관계없이 PD형 오토파일럿으로 인해 기준 회두각을 유지할 수 있다. 그러나 선박은 회두각을 유지하면서 운항은 할 수 있지만 미지의 외란이 인가된다면 선박에 힘과 모멘트가 추가되기 때문에 Figure 5와 같이 선박은 정해진 항로를 벗어나게 된다.
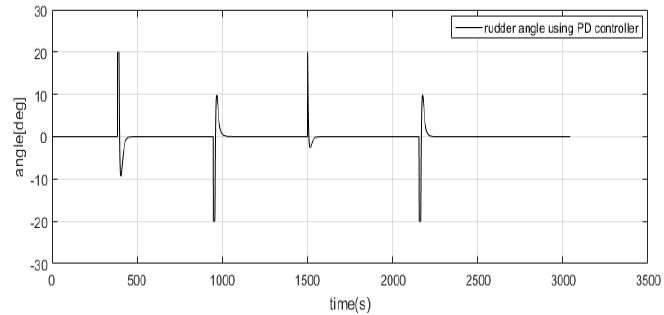
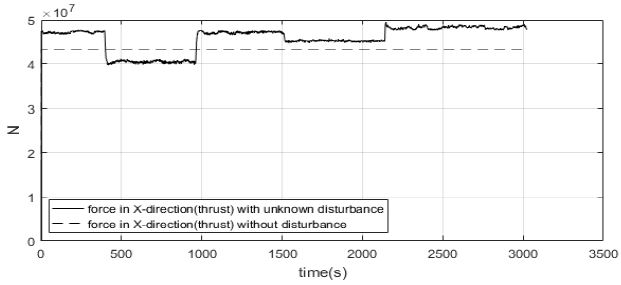
Figure 8은 선박의 조타 명령각을 나타낸 시뮬레이션으로 선박의 안정성을 확보하기 위해 ± 20∘로 제한하였다. Figure 9에서 Figure 11은 미지의 외란이 없는 경우와 있는 경우에 대해 X방향 및 Y방향의 힘과 그리고 Z축에 관한 모멘트를 나타낸 것이다.
Figure 9는 선박이 전진방향 운동을 할 때 선박의 X축 방향의 힘(추력)을 비교한 시뮬레이션 결과이다. 미지의 외란의 영향으로 인해 이동경로에 따라 변하는 힘이 추가되는 것을 알 수 있다. Figure 10과 Figure 11은 선박이 회전운동을 할 때 필요한 힘과 모멘트이다. 선박이 미지의 외란의 영향을 받지 않고 단순히 회전운동을 하는데 필요한 힘과 모멘트에서 미지의 외란 영향으로 인해 발생하는 힘과 모멘트가 추가되는 것을 알 수 있다.
6.3 미지의 외란이 인가된 경우, 인가되지 않은 경우, 퍼지 외란 추정기를 사용한 결과의 비교
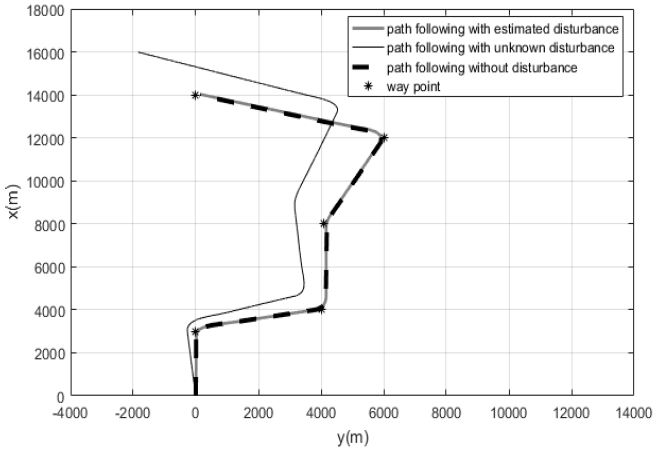
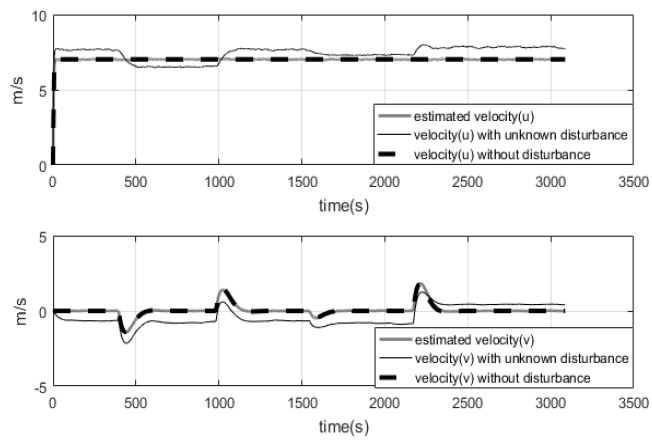
Figure 12는 미지의 외란으로 해류와 파도가 인가된 경우와 이를 퍼지 외란 추정기를 통해 보상시켜 준 선박의 이동경로를 비교한 시뮬레이션이다. 미지의 외란을 퍼지 외란 추정기를 이용하여 보상시켜준 결과 미지의 외란을 인가하지 않은 경우와 유사하게 운항하는 것을 알 수 있다. Figure 13은 미지의 외란이 인가된 경우와 퍼지 외란 추정기로 미지의 외란을 보상시켜준 경우 선박의 속도를 비교한 시뮬레이션이다. 미지의 외란을 퍼지 외란 추정기를 이용하여 보상시켜준 결과 선박의 전진방향 속도 u가 미지의 외란이 인가되지 않은 경우와 유사하게 나오는 것을 알 수 있으며 횡방향 속도 υ역시 미지의 외란이 인가되지 않은 경우와 유사하게 나오는 것을 알 수 있다. 선박의 회두각을 나타내는 시뮬레이션은 PD형 오토파일럿에 의해 기준 회두각을 유지 할 수 있기 때문에 Figure 7로 대체한다. 이와 같이 선박이 전진방향속도 초기 설정값 7m/s 를 유지 하고 횡방향 속도 역시 변침을 제외한 구간에서 속도 성분이 생기지 않는 것은 퍼지 외란 추정기가 미지의 외란으로 선박에 추가되는 힘과 모멘트의 크기를 신뢰성 있게 추정하고 이를 다시 피드백 시켜 주었기 때문이다.
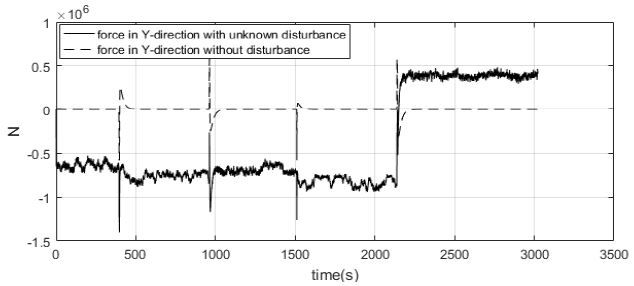
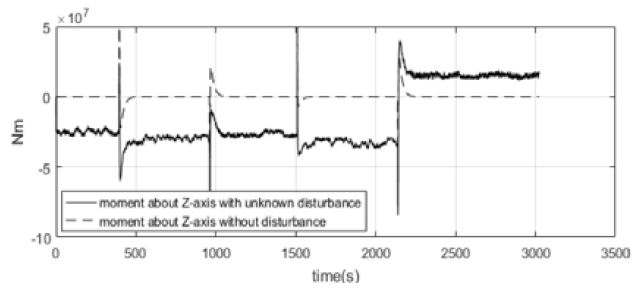
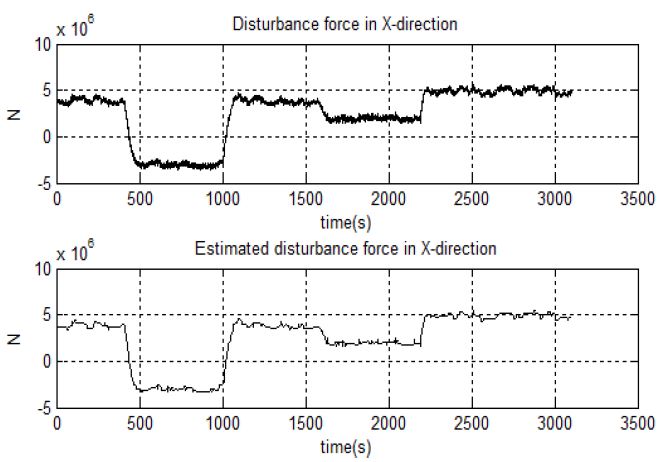
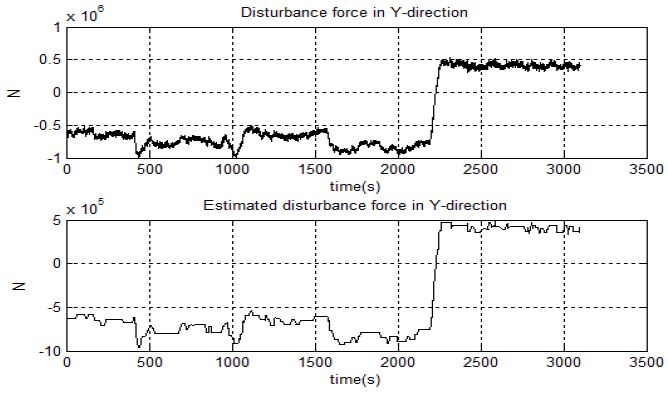
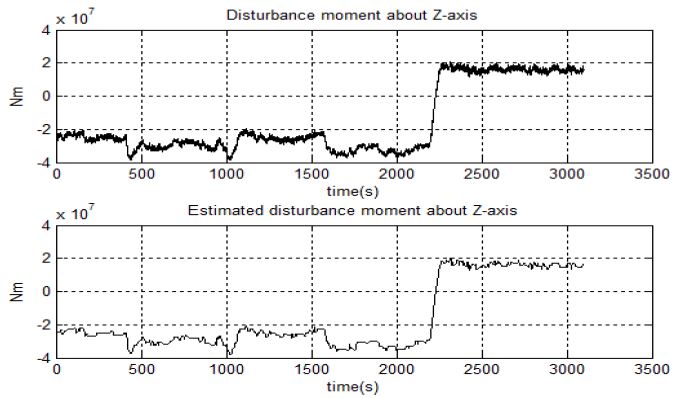
Figure 14에서 Figure 16은 미지의 외란으로 인해 선박에 추가되는 힘과 모멘트와 이때 추가되는 힘 및 모멘트를 퍼지 외란 추정기로 추정한 경우를 비교한 시뮬레이션 결과이다. Figure 14는 X축 방향에 추가되는 힘에 대한 결과이고 Figure 15는 미지의 외란으로 인해 Y축 방향에 추가되는 힘에 대한 결과로서 추정한 힘이 실제로 선박에 인가되는 힘과 유사하게 추정되는 것을 알 수 있다. Figure 16은 미지의 외란으로 인해 Z축 방향에 추가되는 모멘트와 이를 추정한 시뮬레이션으로 선박에 추가되는 모멘트와 유사하게 추정되는 것을 알 수 있다.
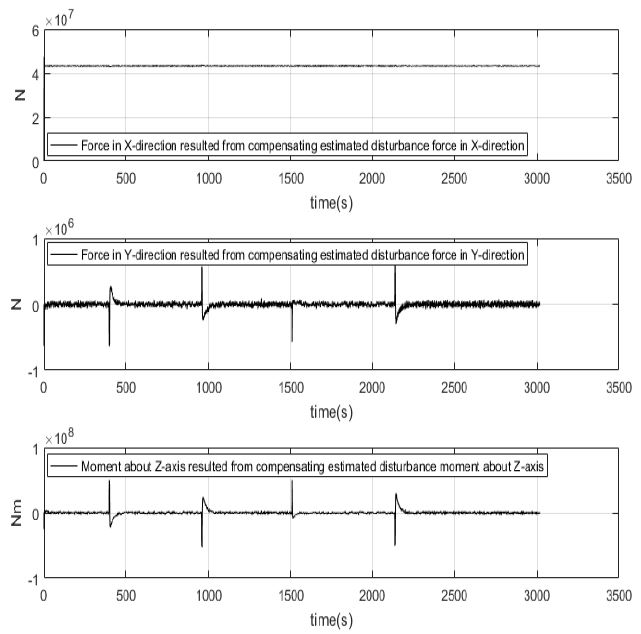
Figure 17은 퍼지 외란 추정기를 통해 미지의 외란을 추정하여 보상시켜준 결과 실제 선박에 미치는 X,Y방향의 힘과 Z축에 대한 모멘트를 나타낸 시뮬레이션 결과이다. 퍼지 외란 추정기를 통해 미지의 외란을 추정하여 보상시켜줌으로써 미지의 외란의 영향으로 선박에 추가되는 힘과 모멘트가 제거되는 효과를 가진다. 그 결과 Figure 9에서 Figure 11의 미지의 외란이 인가되지 않고 단순히 선박이 운동하는데 필요한 힘과 모멘트와 유사하게 나오는 것을 알 수 있다.
7. 결 론
선박이 운항하는데 있어서 중요한 점이 변침점과 다음 변침점 사이의 회두각을 유지하여 정해진 항로를 가능한 벗어나지 않고 최단 시간에 목적지에 도착해야 한다는 것이다. PD형 오토파일럿 시스템으로 인해 선박에 미지의 외란의 인가 여부에 관계없이 기준 회두각은 유지하지만 선박에 추가되는 힘과 모멘트로 인해 정해진 항로에서 벗어나게 되어 에너지 손실이 증가하고 목적지까지의 운항시간이 오래 걸리게 된다. 이와 같은 문제를 해결하기 위해서 본 논문에서는 선박의 외부에서 인가되는 미지의 외란의 영향으로 인해 선박에 추가되는 X,Y축 방향의 힘과, Z축 방향의 모멘트를 보상시켜 주기 위해 퍼지 외란 추정기로 미지의 외란을 추정하고 이를 다시 피드백 시키는 방법을 제안하였다. 시뮬레이션을 통해 제안한 퍼지 외란 추정기의 성능을 검증할 수 있었고 이를 통해 해류와 파도가 외란으로 인가됨에도 불구하고 선박이 정해진 항로를 크게 벗어나지 않고 운항할 수 있는 가능성을 확인하였다.
References
- A. E. Sperry, “Directional stability of automatically steered bodies”, Journal of the American Society of Naval Engineers, 42(2), p284, (1992).
- T. I. Fossen, Recent Development in Ship Control Systems Design, London, USA, Sterling Publications Limited, (1999).
- B. K. Lee, An Optimal Route Decision and LOS Guidance system for Automatic Navigation of Ships, Ph.D. Dissertation, Department of Control and Instrumentation Engineering, Korea Maritime University, Korea, (2005), (in Korean).
- B. K. Lee, and J. H. Kim, “A proposal of an LOS guidance system of a ship for path following”, Journal of the Korean Society of Marine Engineering, 11(4), p363-368, (2005), (in Korean).
- R. Satun, and G. N Roberts, “Approaches to fuzzy autopilot design optimization”, Proceeding of the 4th IFAC conference on Maneuvering and Control of Marine Craft, 30, p77-82, (1997).
- J. H. Kim, Y. S. Ha, and B. K. Lee, “A fuzzy PID controller type autopilot system for route-tracking of ships”, Journal of the Korean Society of Marine Engineering, 30(6), p760-769, (2006), (in Korean).
- T. I. Fossen, Marine Control Systems, Trondheim, Norway, Marine Cybernetics, (2001).
-
J. E. Woo, and J. H. Kim, “A study on translational motion control in integrated control system for ship steering motion”, Journal of the Korean Society of Marine Engineering, 39(1), p32-44, (2015), (in Korean).
[https://doi.org/10.5916/jkosme.2015.39.1.32]

- M. Blanke, Ship Propulsion Losses Related to Automated Steering and Prime Mover Control, Denmark, The Technical University of Denmark, (1981).
-
T. I. Fossen, Handbook of Marine Craft Hydrodynamics and Motion Control, Sussex, England, John Willy & Sons Ltd, (2011).
[https://doi.org/10.1002/9781119994138]

- O. M. Faltinsen, Sea Loads on Ship and Offshore Structures, New York, USA, Cambridge University Press, (1990).
- T. I. Fossen, Guidance and Control of Ocean Vehicles, Sussex, England, John Willy & Sons Ltd, (2011).
-
J. H. Kim, and S. J. Oh, “A fuzzy PID controller for nonlinear and uncertain systems”, Journal of the Soft Computing, 4(2), p123-129, (2000).
[https://doi.org/10.1007/s005000000039]

- S. H. Park, State Estimation and Control of Stochastic System under Unknown Disturbance and Noises, M.S. Dissertation, Department of Control and Instrumentation Engineering, Korea Maritime and Ocean University, Korea, (2016), (in Korean).
- S. K. Seo, State Estimation Algorithm with Fuzzy Estimation Technique for Linear Time Invariant Uncertain Systems, M.S. Dissertation, Department of Control and Instrumentation Engineering, Korea Maritime University, Korea, (2013), (in Korean).