자율무인잠수정의 심도 제어를 위한 유전알고리즘 기반 PD 제어기

1. 서 론

해양탐사용 자율무인잠수정인 AUV (Autonomous Underwater Vehicle)는 해양자원 개발과 군사, 과학조사 분야 등에 대한 관심 고조와 더불어 현재까지도 선진 각국에서 연구개발이 활발히 이루어지고 있다. 우리나라를 포함해 각 국가별로 다양하게 개발된 AUV는 유인 잠수정에 비해 개발과 유지보수 및 운용측면에서는 유리하다. 그러나 해중에서 운동 및 위치 제어성능을 보장할 수 있는 안정된 성능의 제어가 쉽지 않아 이를 개선하고 보완하는 많은 연구들이 수행되어 왔다[1]-[6].

H. S. Kim et al. [1][2]은 Manta 형식의 UUV에 대해 슬라이딩 모드 제어기 설계 기법을, H. Lee et al. [3]과 K. M. Fauske et al. [4]은 칼만필터를 이용하여 센서의 신호를 추정하는 기법을 제안하였다. DAEYANG Electric [5]은 AUV의 제어모드를 자동과 반자동모드로 구분하고, 각각의 모드에 따라 LQ 제어기, PID 제어기, 슬라이딩모드 제어기를 설계하였으며, KORDI [6]은 AUV에 장착된 수중 카메라의 광유동 방정식과 AUV의 운동방정식을 혼합하여 가격함수를 최소화하는 방법으로 비주얼 서보제어기를 구현하였다. 최근에는 최적화 알고리즘과 퍼지기법 및 신경회로망 등을 이용하여 제어기를 설계하는 연구도 진행되고 있다. 이와 같이 많은 연구들이 나름대로 만족할만한 성과를 제시하고 있다. 하지만 이들 연구의 대부분은 제어기 설계 단계에서 작동기의 물리적 한계인 포화(saturation)를 고려하지 않고 제어기 파라미터를 선정하고 있어 성능개선의 여지를 두고 있다. 이를 개선하기 위해 본 논문에서는 제어기 설계 단계에서 작동기의 포화를 고려하여 제어기 파라미터를 선정하고자 한다.

본 논문에서는 AUV 핵심 기술개발에 필요한 운동제어 중 심도제어를 위한 제어기 설계기법을 다룬다. 제어기는 이중 루프의 캐스케이드 제어시스템으로서, AUV의 피치(pitch) 제어기로는 P 제어기를, 핀(fin) 제어기로는 잡음의 영향을 줄이기 위해 수정된 PD 제어기를 적용한다. 각 제어기의 파라미터는 작동기의 한계를 나타내는 포화기를 포함하여 제어시스템의 3가지 목적함수인 제곱오차적분(ISE : Integral of the Square Error), 절대오차적분(IAE : Integral of the Absolute Error) 및 시간곱 절대오차적분(ITAE : Integral of the Time-weighted Absolute Error)를 최소화하는 관점에서 실수코딩 유전알고리즘(RCGAs : Real Coded Genetic Algorithms)[7][8]으로 최적 동조된다.

2. AUV의 운동방정식

해양탐사작업을 목적으로 넓은 탐사영역, 수중에서의 자유로운 운동, 모선이 필요하지 않은 장점 등을 가진 무삭식(untethered) AUV는 축전지에 의한 자체 동력원을 가지며 무선통신을 이용하여 수상모선과 정보를 주고받는 형식이다. 본 장에서는 무삭식 AUV의 한 종류로 운반이 용이하고, 개발비용이 적게 드는 것을 목적으로 WHOI OSL (Woods Hole Oceanographic Institutes Oceanographic System Laboratory)에서 개발한 REMUS (Remote Environmental Monitoring UnitS)의 수학적 운동방정식에 대해서 살펴본다[9][10].

2.1 REMUS의 심도제어를 위한 선형모델

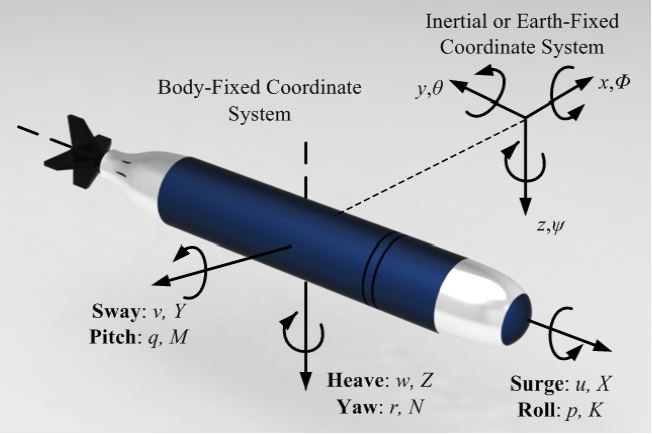
수중운동체로 분류되는 AUV의 운동방정식은 일반적으로 동체의 움직임에 대한 기하학적 요소인 운동학(kinematics), 동체의 관성행렬로 나타내는 강체동역학(rigid-body dynamics), 동체의 움직임을 만들어 내는 힘과 모멘트인 기계학(mechanics)으로 구성된다[11]. REMUS의 6자 유도 비선형 운동방정식은 이렇게 구성된 방정식들을 조합하여 Figure 1 및 Table 1과 같이 SNAME 형식의 물체고정 좌표계에 따라 표현된다[9]. 본 논문에서 언급되는 REMUS의 비선형 운동방정식 모델링과 이를 선형화하여 심도제어에 영향을 미치는 선체운동만을 분리(decoupled)하는 과정은 참고문헌 [9]를 참조하며, 본 절에서는 심도제어를 위해 분리된 선형 운동방정식에 대해서만 살펴보도록 한다.

Figure 1:

Body-fixed and inertial coordinate systems of AUV

Table 1:

The notation for AUV

REMUS의 깊이 방향 동작에 대해서만 고려된 선형 운동 방정식은 식 (1) 및 식 (2)와 같다[9]. 이 때 정상상태에서 REMUS의 속도 U는 1.54 [m/s](약 3 [knots])로 일정하게 이동하고 있다.

$\[ \begin{array}{c}\left(m-X_{\dot{u}}\right)\dot{u}+m{z}_g\dot{q}-X_{u}u-X_{q}q-X_{\theta }\theta =0\\ \left(m-Z_{\dot{w}}\right)\dot{w}-\left(m{x}_g+Z_{\dot{q}}\right)\dot{q}-Z_{w}w-\left(mU+Z_q\right)q=Z_{{\delta }_s}{\delta }_s\\ m{z}_g\dot{u}-\left(m{x}_g+M_{\dot{w}}\right)\dot{w}+\left(I_{yy}-M_{\dot{q}}\right)\dot{q}-M_{w}w+\left(m{x}_{g}U-M_q\right)q-M_{\theta }\theta =M_{{\delta }_s}{\delta }_s\end{array} \]$

(1)

$\[ \begin{array}{c}\dot{z}=w-U\theta \hfill \\ \dot{\theta }=q\hfill \end{array} \]$

(2)

만약 식 (1)에서 무게중심 z_g가 다른 조건들에 비해 매우 작다고 가정하면, 식 (3)과 같이 써지(surge)로부터 히브(heave)와 피치(pitch)를 분리시킬 수 있다.

$\[ \begin{array}{c}\left(m-Z_{\dot{w}}\right)\dot{w}-\left(m{x}_g+Z_{\dot{q}}\right)\dot{q}-Z_{w}w-\left(mU+Z_q\right)q=Z_{{\delta }_s}{\delta }_s\\ -\left(m{x}_g+M_{\dot{w}}\right)\dot{w}+\left(I_{yy}-M_{\dot{q}}\right)\dot{q}-M_{w}w+\left(m{x}_{g}U-M_q\right)q-M_{\theta }\theta =M_{{\delta }_s}{\delta }_s\end{array} \]$

(3)

식 (2)와 식 (3)을 결합하여 상태방정식 형태로 나타내면 식 (4)와 같이 만들 수 있다.

$\[ \begin{array}{c}M\dot{\mathit{x}}-{\mathit{C}}_{\mathit{d}}x=Du\\ M=\left[\begin{array}{c}\begin{array}{cccc}m-Z\dot{w}& -\left(m{x}_g+Z_q\right)& 0& 0\\ -\left(m{x}_g+M_{\dot{w}}\right)& I_{yy}-M_{\dot{q}}& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\end{array}\right],\\ \begin{array}{cc}{\mathit{C}}_{\mathit{d}}=\left[\begin{array}{c}\begin{array}{cccc}{Z}_w& mu+Z_q& 0& 0\\ M_w& -m{x}_{g}u+M_q& 0& M_{\theta }\\ 1& 0& 0& -U\\ 0& 1& 0& 0\end{array}\end{array}\right],& \mathit{D}=\left[\begin{array}{c}{Z}_{{\delta }_s}\\ M_{{\delta }_s}\\ 0\\ 0\end{array}\right]\end{array}\end{array} \]$

(4)

여기서, x는[w q z θ]^T 인 상태벡터이고, u는 핀 제어를 위한 입력으로써 δ_s이다.

식 (4)를 일반적인 상태방정식 표현인 식 (5)로 나타낼 수 있다.

$\[ \begin{array}{c}\dot{\mathit{x}}=Ax+Bu\\ A={\mathit{M}}^{-1}{\mathit{C}}_{\mathit{d}}, B={\mathit{M}}^{-1}D\end{array} \]$

(5)

한편, 히브 속도가 다른 조건들에 비해 매우 작다고 가정하면, 운동방정식은 식 (6)과 같이 더 간단하게 표현하는 것이 가능하다.

$\[ \left[\begin{array}{ccc}{I}_{yy}-M_{\dot{q}}& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}\dot{q}\\ \dot{z}\\ \dot{\theta }\end{array}\right]+\left[\begin{array}{ccc}-M_q& 0& -M_{\theta }\\ 0& 0& U\\ -1& 0& 0\end{array}\right]\left[\begin{array}{c}q\\ z\\ \theta \end{array}\right]=\left[\begin{array}{c}{M}_{{\delta }_s}\\ 0\\ 0\end{array}\right]{\delta }_s \]$

(6)

식 (6)을 일반적인 상태방정식 표현인 식 (5)의 형태로 표현하면 식 (7)과 같이 나타낼 수 있다.

$\[ \begin{array}{c}\dot{\mathit{x}}=Ax+Bu\\ \left[\begin{array}{c}\dot{q}\\ \dot{z}\\ \dot{\theta }\end{array}\right]=\left[\begin{array}{ccc}\frac{M_q}{I_{yy}-M_{\dot{q}}}& 0& \frac{M_{\theta }}{I_{yy}-M_{\dot{q}}}\\ 0& 0& -U\\ 1& 0& 0\end{array}\right]\left[\begin{array}{c}q\\ z\\ \theta \end{array}\right]+\left[\begin{array}{c}\frac{M_{{\delta }_s}}{I_{yy}-M_{\dot{q}}}\\ 0\\ 0\end{array}\right]{\delta }_s\end{array} \]$

(7)

3. 심도 제어용 PD 제어기 설계

3.1 PD 제어기

PID 제어기는 구조가 간단하면서도 안정성이 높고 또 안티와인드업, 수동/자동 무충돌 전환 등의 부가기능과의 결합이 용이하기 때문에 아직도 생산현장에는 PID 제어기가 폭넓게 이용되고 있으므로 본 논문에서도 이를 이용한다[12].

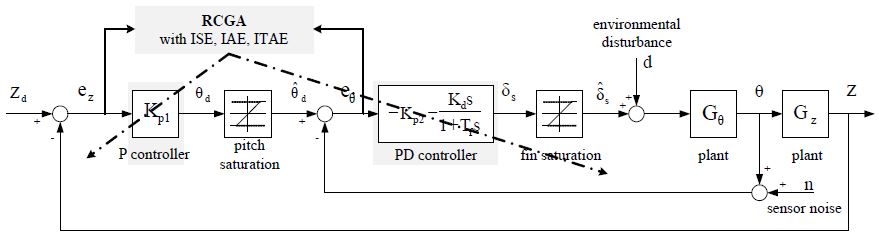
REMUS의 심도 제어기를 Figure 2와 같이 내부(inner loop) 제어시스템의 핀 제어기로는 현장에서 주로 채용하는 식 (8)과 같은 표준 PD 제어기의 수정식을 사용하고, 외부(outer loop) 제어시스템의 피치 제어기로는 식 (9)의 P 제어기를 사용한다.

$\[ \frac{{\delta }_s\left(s\right)}{e_{\theta }\left(s\right)}=-K_{p2}-\frac{K_{d}s}{1+T_{f}s} \]$

(8)

여기서, δ_s는 PD 제어기의 출력으로써 핀의 입력 각도이다. e_θ는 핀의 목표각인 θ_d와 현재 핀의 각인 θ에 대한 오차이다. K_p2는 핀 제어기용 비례제어 이득이고, T_f는 필터 시정수로 T_d /N_d이며, T_d는 미분시간으로 K_d /K_p2이다. N_d는 최대미분이득(maximum derivative gain)으로써 5에서 20 사이에서 경험적으로 정해지는 값이다[13][14]. 이 형은 표준형 PID 제어기에서 일어날 수 있는 미분폭주(derivative kick) 현상을 완화시킬 수 있다.

$\[ \frac{{\theta }_d\left(s\right)}{e_z\left(s\right)}=K_{p1} \]$

(9)

여기서, e_z는 심도오차(Z_d -Z)이고 K_p1은 피치 제어기용 비례제어 이득이다.

식 (8)의 핀 제어기에 음의 부호를 붙여주는 이유는 선체의 피치각과 선미의 핀 각 간에 기호 규칙의 차이가 있기 때문이다. 예를 들어, 양의 방향으로 핀 각(positive sternplane angle)이 움직이면, 핀에 의한 유체의 압력변화로 선체의 후미는 y축에 대하여 음의 방향(negative pitch rate)으로 힘을 받아 움직이게 되고, 결과적으로 선체의 선수는 무게중심을 중심으로 양의 방향으로 모멘트를 생성시키게 된다.

Figure 2에서 Z_d는 목표심도에 대한 입력 명령, Z는 출력으로써 현재 REMUS의 수심을 나타낸다.

Figure 2:

Optimal tuning of the depth controller using a RCGA

4. 제어기 파라미터의 동조

제어기 동조는 전체 제어시스템이 원하는 성능을 갖도록 적절한 방법으로 파라미터를 조정하는 것을 말하며, 식 (8)과 식 (9)의 제어기 파라미터들은 제어 환경에 따라 설정치 추종성능이 최적화되도록 동조된다. 본 논문에서는 Figure 2의 제어시스템에서 설정치 추종 성능이 개선되도록 제어기의 파라미터인 {K_p1 , K_p2, T_d, N_d}을 최적화하는 문제를 다룬다. 설정치를 계단상으로 변경하는 동안 설정치 추종성능을 개선하기 위해 최적화 알고리즘의 한 종류인 RCGA로 동조하게 된다. 심도 제어기의 파라미터를 탐색하기 위해 사용되는 RCGA는 집단이 진화해 가는 동안 개체 간의 우열을 평가하기 위하여 적합도를 필요로 하게 되는데 적합도는 성능지수(목적함수)로부터 계산된다. 탐색된 파라미터에 의한 제어시스템의 성능이 좋고 나쁨을 정량적으로 평가할 수 있는 성능지수로는 식 (10)의 제곱오차적분(ISE), 식 (11)의 절대오차적분(IAE), 식 (12)의 시간곱 절대오차 적분(ITAE) 등을 사용할 수 있다. 본 논문에서는 세가지 성능지수를 모두 고려하였다.

여기서 ϕ_p는 [K_p1, K_p2, T_d, N_d]^T∈R⁴이고, 적분시각 t_f는 이후의 적분값이 무시될 수 있도록 충분히 큰 값이다. 최적화 도구인 RCGA에 의해 탐색되는 동안 ϕ_p는 식 (10) ~ (12)의 성능지수가 최소가 되도록 구해진다.

일반적으로 ISE는 해석이 용이하여 최적제어기 설계 등에 자주 이용되나 오차가 클 때는 큰 벌점을, 작을 때는 작은 벌점을 주는 결과를 초래해 최적해 부근에서 계수의 변화에 둔감하다. 한편 IAE는 오차의 절대크기를 취함으로써 양이나 음의 오차에 균등한 벌점을 부여하는 효과를 주므로 ISE보다 나은 감도를 나타낸다. ITAE는 장시간의 과도현상에 대해 벌점을 주는 매우 유용한 기준으로 IAE나 ISE보다 훨씬 더 변별력이 있으며, 이 적분의 최소값은 시스템의 파라미터들이 변하는 경우에 훨씬 더 잘 정의될 수 있다.

5. 모의실험 및 검토

5.1 모의실험용 데이터와 제어기 파라미터

본 논문의 제어대상인 REMUS의 심도 제어기 설계를 위해 선형화 된 상태방정식은 식 (13)과 같다[9].

$\[ \dot{\mathit{x}}=\left[\begin{array}{ccc}-0.82& 0.00& -0.69\\ 0.00& 0.00& -1.54\\ 1.00& 0.00& 0.00\end{array}\right]\mathit{x}+\left[\begin{array}{c}-4.16\\ 0.00\\ 0.00\end{array}\right]{\delta }_s \]$

(13)

RCGA를 사용하여 REMUS의 심도 제어를 위한 제어기의 파라미터를 Figure 2와 같이 세 개의 성능지수별로 탐색하였다. 이때 사용된 RCGA의 제어변수로서 집단의 크기는 20, 재생산 계수는 1.8, 교배확률은 95%, 동적 돌연변이 확률은 20%가 사용되었고, 미지의 제어기 파라미터들을 탐색하기 위한 구간은 –10≤K_p1≤10, -10≤K_p2≤10, 0.01≤T_d≤10, 5≤N_d≤20으로 한다. 이 때 초기의 동체는 수면 0[m]에서 운항하고 있으며, 목표 심도를 수심 10[m]로 명령한다. 심도 제어시스템에서 포화기로 작용하는 핀각의 작동은 ±9[°], 피치각의 운전 가능 범위는 ±15[°], 피치각의 변화 속도는 ±1[°/sec]로 제한된다. 제안된 방법으로 얻어지는 제어기 파라미터들의 정밀도는 초기집단의 선택에 따라 달라질 수 있어 독립된 씨드(seed)로 생성된 초기집단으로 5회 모의실험을 실시하고 그 결과를 평균하였다. Table 2의 제어기 파라미터들은 참고문헌 [9]에서 제시한 극배치법에 의해 선정한 것과 RCGA에 의해 동조된 결과를 나타낸 것이다.

Table 2:

Tuned parameters of the controllers

5.2 성능 비교

제어기의 파라미터 동조시 포화기의 한계를 고려하지 않은 경우와 고려한 경우를 비교하고, 수정된 미분제어기의 잡음에 대한 성능을 시뮬레이션을 통해 검증한다.

5.2.1 포화기를 고려하지 않고 파라미터를 탐색한 경우

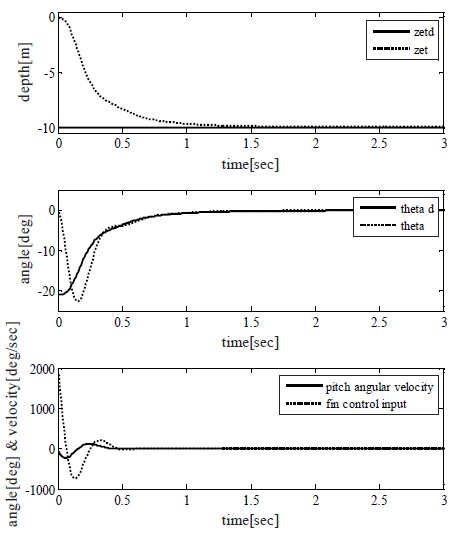
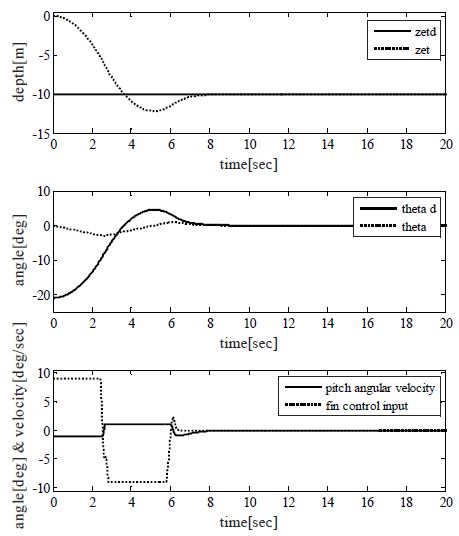
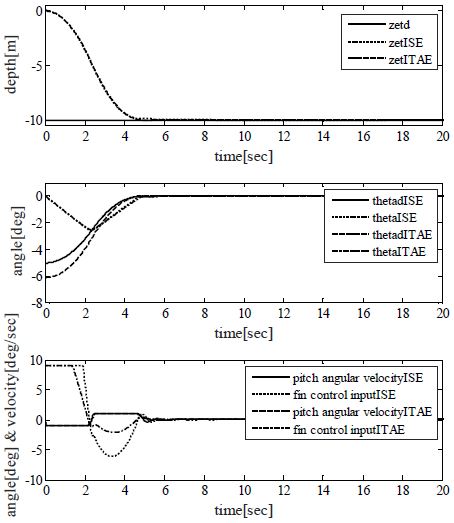
Figure 3은 포화기를 고려하지 않고 ISE 성능지수에 의해 제어기 파라미터들을 탐색한 경우의 심도 설정치를 0[m] → -10[m] 변경에 대한 응답을 보인 것이다. 성능은 2.5초 이내에 설정치인 심도 10[m]에 도달하는 것을 알 수 있다. 그러나 응답에 대한 제어 입력과 핀의 실제 작동상태를 살펴보면 현실적으로는 작동이 불가능한 것을 알 수 있다. Figure 4는 Figure 3에서 사용된 동일한 제어기 파라미터들을 포화기가 설치된 시스템에 적용시킨 결과이다. 제어입력과 핀의 실제 작동상태는 현실적으로 작동이 가능한 포화기의 범위 내에서 작동하고 있으나, 오버슈트가 발생하면서 약 8.9[sec] 이후에 설정치인 심도 10[m]에 도달하고 있다. Table 3은 각 경우를 시뮬레이션 한 성능을 수치화 시킨 것으로 오버슈트(M_p), 상승시간(t_r), 정착시간(t_s), 설정치에 대한 정상상태 오차(e_ss)이며, IAE value는 설정치와 응답의 차이를 적분한 면적을 의미한다.

Figure 3:

Depth tracking response using GA ISE, excluding saturator for pitch, pitch rate and fin control

Figure 4:

Depth tracking response using GA ISE, including saturator for pitch, pitch rate and fin control

Table 3:

Performance of depth control system excluding constraints

5.2.2 포화기를 고려하여 파라미터를 탐색한 경우

핀의 작동, 피치각 및 피치의 각속도가 제한되는 포화기를 고려하여 탐색된 제어기 파라미터들에 대하여 시뮬레이션한 결과를 살펴본다.

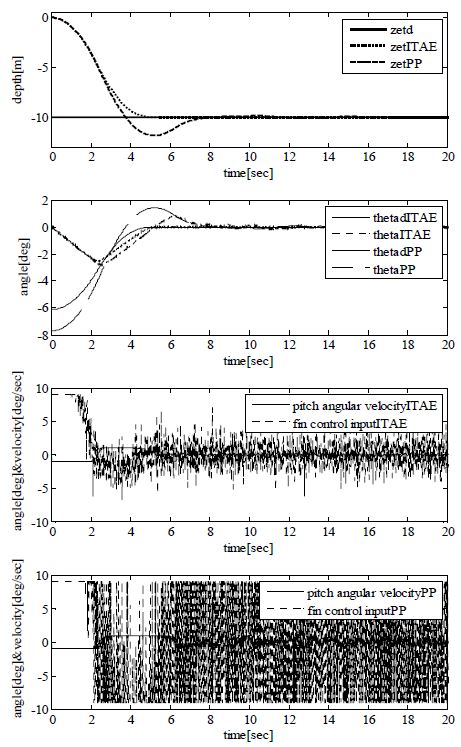
Figure 5는 포화기가 고려된 시스템을 세 가지 성능지수가 각각의 목적함수를 최소화 시키도록 탐색된 제어기 파라미터들을 사용하여 명령심도(0[m] → -10[m])에 대한 응답을 비교한 것이다. Figure 4와 비교하여 오버슈트는 거의 없으며, 정착시간에서 좀 더 빠른 동작을 보여주고 있다. ITAE의 경우 시뮬레이션 결과상으로는 ISE(IAE)의 경우와 비슷한 결과를 보이나 ISE(IAE)에 비해 상승시간과 정착시간에서 좀 더 빠른 동작을 보여주고 있다. Table 4는 Figure 5의 성능을 정량화한 것이다.

Figure 5:

Depth tracking response using GA ISE and ITAE with saturator for pitch, pitch rate and fin control

Table 4:

Performance of depth control system excluding constraints

5.2.3 잡음의 영향

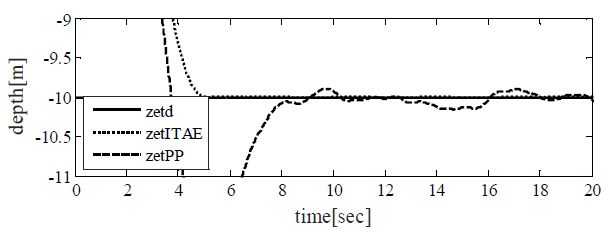
실제 제어 환경에서는 신호계측 시 항상 센서로부터 잡음이 유입될 가능성이 있으므로 제어기 설계시 이 점을 유의할 필요가 있다. 제안한 방법의 잡음에 대한 영향을 알아보기 위해 Figure 6은 센서에 정규잡음 N(0, 0.05)이 유입되는 것으로 가정하고 심도 변경에 대한 응답을 구해 그린 것이다. 미분 폭주현상을 감안하지 못하고 극배치법에 의해 구해진 파라미터에 대한 응답과 비교하여 수정된 미분제어기가 잡음에 대한 영향을 줄이고 있는 것을 알 수 있다. Figure 7은 잡음의 영향으로 인해 심도 설정치 부근을 확대시킨 것으로써 극배치법에 의해 구해진 파라미터의 경우 잡음에 의해 핀 제어 입력이 영향을 받아 설정치 부근에서 상대적으로 많은 움직임을 보이고 있다.

Figure 6:

Depth tracking responses when noise N (0, 0.05) exist

Figure 7:

Depth tracking response when noise N (0, 0.05) exist

6. 결 론

본 논문에서는 REMUS의 심도 제어를 위해 내부 제어시스템의 핀 제어기로는 미분 폭주 현상을 완화시키기 위해 수정된 PD 제어기를 사용하고, 외부 제어시스템의 피치 제어기로는 P 제어기를 사용하였다. 이 때 제어대상 시스템의 기계적 한계를 고려하여 핀의 작동과 피치 운전이 실현가능한 작동 범위 내에서 운전될 수 있도록 포화기를 설치하여 목표 심도에 도달할 수 있도록 제어기의 파라미터들을 동조하였다. 최적화 도구의 한 종류인 RCGA를 이용하여 심도 제어시스템의 설정치 추종성능이 만족되도록 제어기 파라미터들을 탐색할 때, 평가함수로는 ISE, IAE, ITAE 세 가지 성능지수를 사용하였다. 이렇게 구성된 새로운 평가함수의 값이 최소가 되는 관점에서 동조된 제어기의 파라미터들을 REMUS 심도 제어시스템에 적용하였다. 포화기를 고려하여 동조된 제어시스템의 파라미터들을 시뮬레이션한 결과, 현실적으로 작동 가능한 범위 내에서 제어대상을 운전할 수 있었다. 또한, 잡음의 영향을 고려한 PD 제어기를 적용한 결과 잡음 제거의 효과가 탁월하다는 것을 확인 할 수 있었다.

References

• H. S. Kim, K. H. Sohn, and S. K. Lee, “A study on the sliding mode controller of Manta type UUV,", Proceedings of the Korean Institute of Navigation and Port Research Conference, p3-4, (2011), (in Korean).
• H. D. Kim, J. Y. Kim, S. H. Kim, and S. K. Lee, “A study of the control system on the manta-type UUV”, Journal of Navigation and Port Research, 35(5), p359-363, (2011), (in Korean). [https://doi.org/10.5394/kinpr.2011.35.5.359]
• H. Lee, and S. G. Lee, “A study on position control of ship using Kalman filter,", Proceedings of the Korean Institute of Navigation and Port Research Conference, p74-76, (2012), (in Korean).
• K. M. Fauske, F. Gustafsson, and O. Hegrenaes, “Estimation of AUV dynamics for sensor fusion”, IEEE Information Fusion, 10th 2007 International Conference on 9th-12th, (2007). [https://doi.org/10.1109/icif.2007.4408044]
• DAEYANG Electric, Development of Technologies for Navigation and Manipulator System of a Semi-Autonomous Underwater Vehicle: Ministry of Science and Technology, (2003), (in Korean).
• Korea Ocean Research & Development Institute, Development of an Advanced Deep-Sea Unmanned Underwater Vehicle (2): Ministry of Oceans and Fisheries, (2003), (in Korean).
• G. G. Jin, and S. R. Joo, “A study on a real-coded genetic algorithm”, Journal of Institute of Control, Robotics and Systems, 6(4), p268-275, (2000), (in Korean).
• G. G. Jin, Genetic Algorithms and Their Applications, 2nd edition, Seoul, Korea, KyoWooSa, (2004), (in Korean).
• T. J. Prestero, Verification of a Six-Degree of Freedom Simulation Model for the REMUS Autonomous Underwater Vehicle, M.S. Thesis, Massachusetts Institute of Technology/Woods Hole Oceanographic Institution, Department of Ocean and Mechanical Engineering, USA, (2001). [https://doi.org/10.1575/1912/3040]
• M. Purcell, C. von Alt, B. Allen, T. Austin, N. Forrester, R. Goldsborough, and R. Stokey, “New capabilities of the REMUS autonomous underwater vehicle”, Proceedings of the MTS/IEEE Oceans 2000, 1, p147-151, (2000).
• T. I. Fossen, Guidance and Control of Ocean Vehicles, NY, USA, John wiley & Sons, (1994).
• K. J. Åström, and T. Hägglund, PID Controllers: theory, design and tuning, NC, USA, ISA Press, (1995).
• O. Aidan, Handbook of PI and PID Controller Tuning Rules, (3rd Edition), World Scientific, (2009). [https://doi.org/10.1142/9781848162433]
• C. Bohn, and D. P. Atherton, “An analysis package comparing PID anti-windup strategies”, IEEE Systems Magazine, 15(2), p34-40, (1995). [https://doi.org/10.1109/37.375281]