수직 GMA용접에서 V그루브 비드 폭 예측에 관한 연구

1. 서 론

국내에서 용접기술은 이론적인면 보다는 기능적인 개념으로 인식되어 왔기 때문에 용접기술 개발이 늦어졌으며, 이로 인하여 최근에는 전문적인 용접기술 인력의 부족현상이 나타나고 있다. 또한 전문적인 용접관련 기술들은 대부분 외국으로부터의 도입에 의존하고 있는 실정이며, 이러한 문제는 용접공정에 소요되는 경비가 막대하게 증가하고 있다. 이를 극복하기 위해 고효율, 고생산성 저비용 아크 용접의 효과를 얻기 위해 수작업으로만 이루어지던 아크 용접공정을 자동화하기 위한 많은 시도가 이뤄지고 있다. GMA 용접을 이용한 생산공정에서 대상제품의 품질을 제어하기 위해서는 주요 인자들과 관련된 공정변수를 측정하여 변수들만으로 용접품질을 제어해야 하지만 실제 공정에서는 어려운 실정이다. 또한 최근 들어 산업의 경향이 새로운 방향으로 변화하고 있으며 기존의 대량생산방식이 이미 포화상태에 다다르고 있다. 사람들의 소비 경향도 무조건 값싼 제품을 찾는 것이 아니라, 자신의 필요에 따라 원하는 제품을 찾고 있는 경향을 나타낸다. 이러한 생산기술과 생산제품의 변화는 생산라인의 변화를 필요로 하는데 기존의 고정적 기능의 자동화 시스템으로 소비자의 요구사항이나 생산라인 변화를 만족시키지 못한다. 특히 GMA용접은 일반 용접자세와 다르게 용접속도가 느려지기 때문에 슬래그가 용접부에서 빠져나오지 못하고 중간에 응고되는 경우가 발생되는데, 이는 용융 슬래그가 계속 용융지에 머무르게 되고 이러한 현상이 시간이 지남에 따라 용융지에 많은 슬래그가 쌓이게 되어 전기 전도도가 떨어져 불연속적인 아크가 발생하게 된다. 아크가 불안하게 진행되면 스패터 발생량이 많아지고 슬래그가 동시에 비산되어 토치 끝단에 융착되기 때문에 용접 와이어의 송급을 방해하여 용입불량 및 기공발생 등의 이유로 용접안정성을 확보할 수 없다. 따라서 다양한 수학적 모델 및 알고리즘을 개발하여 수직 GMA 용접공정의 비드형상을 예측하고, 용접공정 현장에 즉시 적용시키기 위한 연구들이 시도되고 있다.

일반적으로 용접품질은 모재, 용가재, 용접봉, 모재의 예열과 후열 등과 같이 용접 전후에 수행되는 용접준비 작업에 따라 달라진다. 특히 용접 중에 용접품질은 아크의 안정성과 금속이행(Metal transfer) 중에 용접전류, 아크전압, 아크길이, 보호가스, 단락주파수, 와이어 송급속도 등의 변화에 큰 영향을 받는다. 또한 용접공정 변수인 용접전류와 아크전압은 용접상태에 따라 신호파형이 변화하기 때문에 파형 균일성을 가지고 아크의 안정성 및 용접품질을 판단하고 있다. 용접품질을 용접전류와 아크전압의 파형을 이용하여 평가하는 기존의 연구들은 대부분 용접공정 변수의 평균값, 표준편차 및 단락 주파수를 사용하고 있다[1]-[6].

기존의 연구에서 Ludewig[7]은 용접전류 또는 아크전압의 표준편차, 단락 주파수 및 신호들의 시간에 대한 변화율의 평균값을 이용하여 용접품질을 평가하였다. Quinn[8]은 용접전류, 아크전압 및 용접저항의 평균값을 사용하여 용접품질을 평가하였으며 Adolfsson[9]은 용접전류 및 아크전압 신호의 평균, 표준편자, 분산과 단락주파수, 단락시간 등을 분석하여 용접품질을 평가하였다.

Raveendra와 Parmar[10]는 CO2를 차폐 가스로 사용한 FCA(Flux Cored Arc)용접에서의 비드 폭과 비드형태를 예측하는 수학적 모델을 제시했다. 용접전압, 아크전류, 용접속도, 노즐-모재 간격, 토치각도 등을 함수로 사용하였고 부분 계수법(Fractional factorial technique)과 다중 회귀법(Multiple regression technique)을 이용하여 실험을 수행하였다. 그 결과 수학적 모델이 비드 폭 예측에 효과적인 수단이며 좋은 비드 특성을 얻기 위한 제어 변수값을 예측하는데 유용하다는 사실을 보여주었다.

Chandel[11]은 처음으로 수학적 모델을 GMA(Gas Metal Arc)용접 공정에 적용하여 평판 용접에서의 공정변수와 비드 폭의 관계를 조사하고 Kim[12]은 GMA용접 공정에 적용하여 맞대기 용접에서의 공정변수와 비드 폭의 관계를 조사하여 아크전류가 비드 폭에 가장 큰 영향을 미치며 실험 결과에서 도출한 수학적 모델을 비드 폭 예측에 사용할 수 있다는 사실을 확인하였다.

하지만 기존의 연구들은 측정변수와 용접품질 사이의 상관관계를 분석하기 위해 다양한 분석기법들이 사용되고 있지만 많은 시간과 비용이 필요하며, 복잡한 평가절차로 인한 한계를 가지고 있다.

본 연구에서는 입열량 증가에 따른 물성이 저하될 가능성이 있으며, 비드폭이 넓어지면 용접 결함이 증가하게 된다. 따라서 수직 GMA용접에서의 공정변수 변화에 따른 V그루브의 비드 폭을 예측하고자 2차 회귀방정식, GDBP 및 LMBP 신경회로망을 포함하여 다양한 수학적 모델 및 알고리즘을 개발하고, 개발된 예측 모델의 신뢰성을 검증하기 위하여 실제 용접실험에서 얻은 비드 폭과 상호 비교·분석하여, PAM(Predictive Ability of Model)분석을 통해 비드 폭 예측 정확도를 확인하였다.

2. 용접 데이터 수집을 위한 용접실험

2.1 용접실험 구성 및 방법

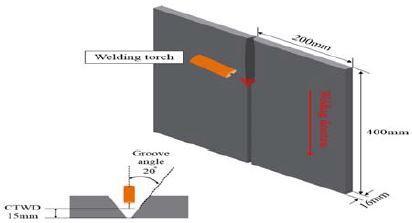
수직 GMA 용접공정에서 V그루브의 비드 폭을 예측하기 위해 500A급 GMA 용접기와 토치 구동부, 와이어 송급장치, 수직형 용접 JIG로 용접시스템을 Figure 1과 같이 구성하여 용접데이터를 수집하였다.

Figure 1:

Experimental setup for vertical GMA welding process

본 실험을 위하여 용접모재는 SS400 재질의 일반구조용 압연강재를 사용하였으며, 400mm × 200mm × 16t의 규격인 시험편을 제작하였다. 또한 시험편의 용접하고자 하는 표면에 녹, 스케일, 산화물 등 이물질이 용접결함의 원인이 되지 않도록 Stainless wirebrush로 깨끗이 닦은 후에 용접실험을 수행하였다. GMA 용접을 수행하기 위한 개략도를 Figure 2에 나타냈으며, 실험에 사용된 시험편의 기계적 성질 및 화학적 조성은 Table 1과 Table 2에 각각 나타내었다.

Table 1:

Mechanical properties of base metal

Table 2:

Chemical compositions of base metal

Figure 2:

A schematic diagram for vertical GMA welding process

실험은 공정변수에 따라 변화되는 비드 폭을 예측 및 분석하기 위해 입력변수로는 용접전류, 아크전압, 용접속도로 선정하여 용접실험을 수행하였다. 출력변수로는 용접부 비드 폭을 선정하였으며, 그 외에 기타 변수들의 경우 고정한 V그루브 각도, 전극간 거리, 용접토치를 선정하여 실험을 진행하였다.

용접실험계획은 반응표면설계 중 박스-벤컨법 (Box-Behnken) [13]을 적용하여 3요인 3수준 인자분석을 수행하고자 총 15회의 실험조건을 생성하였으며, 박스-벤컨법은 3요인 이상일 때 주로 사용하고 요인수가 같은 경우 꼭지점에서 실험을 수행하지 않는 특징을 가지고 있다. 따라서 중심 합성 설계보다 실험횟수가 적어 비용이 많이 들거나 현실적으로 실험이 불가능할 경우에 유용하게 사용할 수 있는 장점들을 포함하고 있다. 초층(1 Pass) 용접조건은 120A, 20V, 30cm/min 으로 용접하고 Fill pass는 Table 3과 같이 공정변수의 실험변수 및 수준을 설정하였다. 본 용접실험은 Table 4와 같이 15개의 실험조건을 사용하였다.

Table 3:

Vertical GMA welding parameters and their levels (2nd~5th pass)

Table 4:

Experimental plan (2nd~5th pass)

3. 실험결과 및 고찰

3.1 V 그루브 비드 폭 측정 결과

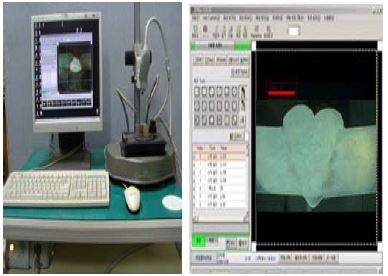
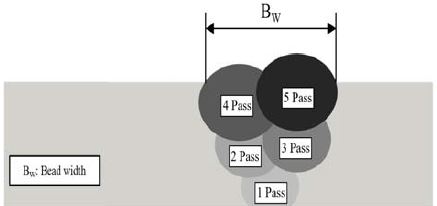
용접조건에 따라 비드 폭에 미치는 영향을 판별하기 위하여 단면형상(Macro)를 촬영하여 비드단면 특성을 분석하였으며, 비드 폭 측정을 위해 용접이 완료된 시험편의 가로축 중간부분을 레이저 절단기를 사용하여 60×30mm의 크기로 절단하고 단면부를 연삭한 후 폴리싱(Polishing) 하였다. 시험편의 단면형상을 명확하게 나타내기 위해 90% Ethanol + 10% Nitric 용액을 혼합하여 단면부에 에칭 작업을 수행한 후 모재에 적절한 용입이 이뤄졌는지 확인하기 위하여 광학 현미경 시스템(SOMETECH社, SV-35)을 이용하였다. 10배의 광학 현미경으로 사진을 현상하여 스캐닝 후 컴퓨터에서 좌표점을 주어 양쪽을 측정하였으며, 총 15개 시험편의 단면 비드크기를 측정하였다. Figure 3과 Figure 4는 비드 폭 측정에 사용된 현미경 및 단면의 비드 폭의 크기를 측정하는 화면과 비드 폭 측정 모식도를 나타냈으며, 측정된 결과인 비드 폭과 각 용접조건에 대한 대표적인 단면 비드형상을 Table 5에 나타냈다.

Figure 3:

Measurement of bead geometry

Figure 4:

Measurement model of bead section

Table 5:

Experimental results data of the vertical GMA welding

3.2 2차 회귀분석을 이용한 비드 폭 예측모델 개발

반응표면분석법이란 여러개의 입력변수 x₁, x₂, x₃, ⋯, x_k가 복합적인 작용을 함으로써 출력변수 y에 영향을 주고 있을 때 이러한 반응의 변화가 이루는 반응표면에 대한 통계적인 분석방법이다. 다시 말해서 입력변수들과 출력변수 간의 함수관계를 데이터로부터 추정하여 입력변수들의 값의 변화에 따라 출력변수의 값이 어떻게 달라지는가를 예측하고 입력변수의 어떠한 값에서 반응량이 최적화로 정의한다. 그러므로 가장 적은 수의 실험으로 가장 좋은 정도를 주는 실험계획법이 무엇인가를 고찰하고, 데이터 분석을 통하여 추정되는 적합한 반응표면의 통계적인 성질을 규명할 수 있는 특징을 가지고 있다.

입력변수 x₁,x₂,x₃,⋯,x_k와 출력변수 y간의 함수관계는 식 (1)과 같이 나타내며, 출력변수인 비드 폭의 예측값이 입력변수와 비선형적인 관계를 가정했을 경우 이를 2차 선형회귀모델(Second order regression model)로 식 (2)로 나타낼 수 있다.

$\[ Y=f\left(I,V,S\right) \]$

(1)

$\[ y={\beta }_0+\sum _{i=1}^k{\beta }_i{x}_i+\sum _{i\le j}^k{\beta }_{ij}{x}_i{x}_j+ϵ \]$

(2)

여기서 Y는 비드 폭, I는 용접전류, V는 아크전압, S는 용접속도를 나타내며 식 (2)은 최소제곱법(Method of least squares)에 의해 식 (3)와 같이 나타낼 수 있다.

$\[ \widehat{y}=\widehat{{\beta }_i}+\sum _{i=1}^k\widehat{{\beta }_i}{x}_i+\sum _{i\le j}^k\widehat{{\beta }_{ij}}{x}_i{x}_j+c \]$

(3)

본 연구에서는 입력변수의 수가 3개 즉, k=3이므로 식(4)와 같이 나타낼 수 있다.

$\[ \widehat{y}=\widehat{{\beta }_0}+\widehat{{\beta }_1}{x}_1+\widehat{{\beta }_2}{x}_2+\widehat{{\beta }_3}{x}_3+\widehat{{\beta }_{11}}{x}_1^2+\widehat{{\beta }_{22}}{x}_2^2+\widehat{{\beta }_{33}}{x}_3^2+\widehat{{\beta }_{12}}{x}_1{x}_2+\widehat{{\beta }_{13}}{x}_1{x}_3+\widehat{{\beta }_{23}}{x}_2{x}_3+\mathrm{c} \]$

(4)

여기서, $$ \widehat{y}$$는 비드 폭의 추정량이고, x_i는 입력변수(용접전류, 아크전압, 용접속도)들의 Coded unit이며, $$ \widehat{{\beta }_0},\widehat{{\beta }_i,}\widehat{{\beta }_{ij}}$$ 는 각각 β₀, β_i, β_ij의 최소 제곱추정량을, ϵ은 오차를 나타낸다.

위 회귀모델(Regression model)을 구하기 위해서는 많은 실험을 통해 관련 데이터를 얻어야한다. 이와 같이 실험을 통해 관련 데이터를 얻으려고 한다면, 수많은 실험의 시행착오와 경제적인 손실이 발생할 수 있으므로 이러한 손실을 줄이고자 2차 회귀모델을 잘 반영하는 실험계획법의 반응표면분석법 중 중심합성계획법을 사용하였으며, 각 항의 계수는 MINTAB을 이용하여 계산하였다.

회귀계수와 식 (4)를 이용하여 비드 폭에 대하여 개발된 2차 회귀모델은 식 (5)와 같다.

$\[ B_W^{2nd}=2.899+0.299I-0.106V-0.023S+0.029I^2-0.001V^2-0.004S^2+0.005IV-0.053IS-0.003VS \]$

(5)

여기서, $$ B_W^{2nd}$$는 비드 폭을 나타낸다.

선정된 수학적 모델의 정확성을 비교·분석하기 위하여 분산분석(Variance technique)을 수행하였으며, Table 6는 식(3)에서 선정된 방정식들의 산출표준오차(Standard error of estimate), 복합상관계수(Coefficient of multiple correlation) 그리고 결정계수(Coefficient of determination)를 나타낸다.

Table 6:

Analysis variance test

복합상관계수와 결정계수를 통해 간단한 2차 회귀모델 만으로도 상당히 정확하게 비드 폭을 예측하고 있기 때문에 선형적인 관계에 있는 것을 확인하였으며, 전체적인 비드 형상에 대해서 예측성이 매우 높음을 확인하였다.

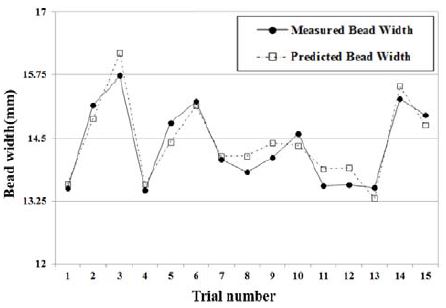
이 중 결정계수는 선형모델의 입력변수를 이용하여 출력변수의 변동(Variability)의 정도를 나타내는 지수로써, 비드 폭의 경우 2차 회귀방정식에 대해 결정계수 값은 98.5%로 나타났다. 2차 회귀의 경우 비드 폭을 예측하는데 매우 뛰어난 성능을 보임을 확인할 수 있다. 또한 개발된 각각 모델의 검증을 위하여 개발한 회귀방정식을 이용하여 실험값과 예측값의 비교·분석을 수행하였으며 그 결과를 Figure 5에 나타냈다.

Figure 5:

Comparison and analysis of predicted values of bead width

3.3 신경회로망을 이용한 비드 폭 예측모델 개발

함수근사법을 위해 입·출력 파라미터 사이의 비선형 매핑이 필요한 연구 분야에서는 신경회로망이 폭넓게 사용되고 있다. 본 연구에서는 수직 GMA 용접공정에서의 V그루브 비드 폭을 예측하기 위하여 비드 폭에 대한 용접전류, 아크전압, 용접속도 등 복잡하고 상호작용이 매우 큰 공정 변수를 매핑하는 도구로 신경회로망을 적용하였다. 비드 폭 예측의 성능을 향상시키기 위하여 가장 적합한 신경회로망을 선정 및 적용하기 위하여 다층퍼셉트론 신경회로망은 역전파 (Back-Propagation) 알고리즘과 Levenberg-Marquardt 알고리즘 2가지를 적용하여 비드 폭 예측모델을 개발하였다.

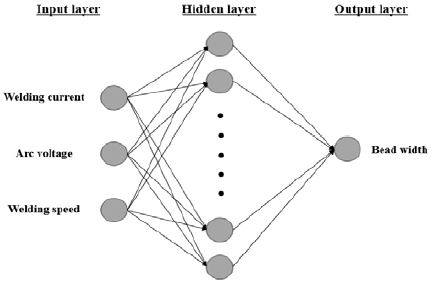
수직 GMA 용접공정에서 비드형상에 영향을 주는 여러 변수가 있지만 본 연구에서는 주요인자인 용접전류, 아크전압, 용접속도를 고려하였으며, 3개의 입력변수에 대한 출력 비드형상을 매핑하기 위해 입력층에는 3개, 출력층에는 1개의 뉴런을 가진 3층 전방향신경망을 Figure 6에 나타냈다.

Figure 6:

Design of optimal neural network for bead width prediction

본 연구에서 네트워크 개발과 학습은 상용 수치해석 프로그램인 MATLAB을 이용하고 각각의 신경회로망 학습에 사용된 데이터는 초층 용접을 제외하고 다층 용접의 비드형상을 측정한 3회 반복실험에서 획득한 15개 조건에 대한 45개의 데이터를 이용하였다. 학습된 신경회로망을 검증하기 위하여 3회 반복실험을 통한 평균 비드 폭 데이터를 토대로 용접 비드 폭을 예측하였다. 신경회로망 구조에서 은닉층의 수는 최적화문제에서는 은닉층의 수가 1개만으로도 충분하므로 은닉층 수는 1개로 고정하였으며, 신경회로망의 은닉층 뉴런수와 반복횟수는 계속 증가시키면서 학습하여 학습오차를 감소시키다가 학습오차의 변화가 안정화되는 부분에서의 뉴런의 수와 반복횟수를 선정하여 신경회로망의 구조를 결정하였다. 신경회로망의 학습에 사용된 입력변수는 용접전류, 아크전압, 용접속도 등 3가지를 이용하였으며, 비드 폭을 출력변수로 선정하였다. 네트워크의 학습 신경회로망에 사용된 사이즈는 1,000이고 초기 오차 목표는 무작위로 선택되도록 구성하였다.

3.3.1 GDBP(Gradient Descent Back-Propagation) 알고리즘

다층 퍼셉트론 신경회로망의 역전파 알고리즘은 원하는 목표값(d)과 실제 출력값(o) 사이의 오차제곱합으로 정의된 비용함수(Cost function) E의 값을 최급강하법(Gradient-descent method)에 의해 최소화 하는 방향의 학습법이다.

$\[ E=\sum _p{E}_p,\left(E_p=\frac{1}{2}\sum _j{\left(d_{pj}-o_{pj}\right)}^2\right) \]$

(6)

여기서 p는 p번째 학습패턴이며, E_p는 p번째 패턴에 대한 오차, d_pj는 p번째 패턴에 대한 j번째 요소, 그리고 o_pj는 실제 출력의 j번째 요소를 나타낸다.

GDBP 알고리즘은 관리학습 패턴의 대표적인 신경회로망 모델로서, 오차 역전파라고 하는 기법을 처리 유닛(Unit)에 적용한 것이다. 출력층의 각 처리 유닛간의 연결강도를 수정함으로서 다음 학습 시 목표값에 더욱 근접된 출력값을 갖게 한다. 출력값이 목표값과 유사하게 될 때까지 학습을 반복하게 되며, 학습이 끝나면 학습한대로 결과를 출력하게 된다. 즉, 주어진 패턴이 반복학습을 통하여 지식을 획득할 뿐만 아니라 규칙이 알려지지 않은 상황에서 패턴과 특성을 발견할 수 있는 능력을 갖고 있다. 최급강하법에 의한 오차 역전파 알고리즘(GDBP)을 이용한 신경회로망의 학습조건을 위한 네트워크 구조 설정은 Table 7에 나타냈으며, GDBP 알고리즘을 이용한 예측성능 결과를 Table 8과 같이 나타냈다.

Table 7:

GDBP algorithm parameter and their levels

Table 8:

Result of GDBP algorithm prediction performance

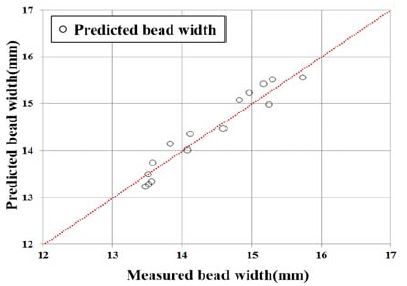
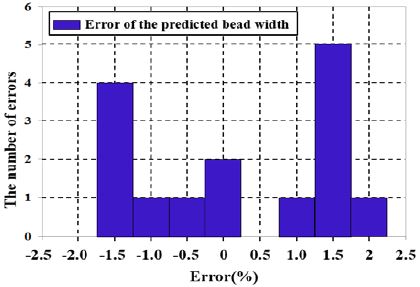
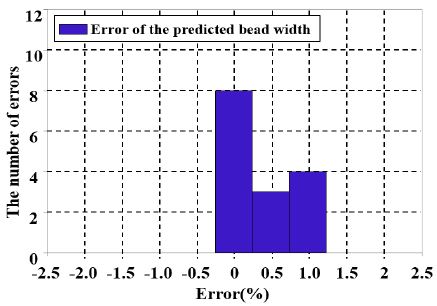
GDBP신경회로망을 이용하여 예측된 비드 폭과 수직 GMA 용접실험을 통해 측정된 비드 폭을 비교한 것과 그에 따른 오차율을 히스토그램을 통해 빈도수 도출 그래프를 Figure 7과 Figure 8과 같이 나타냈다. 다양한 신경망의 RMS오차를 비교·분석한 결과 3-10-2구조의 신경망을 토대로 최소 RMS오차는 10개의 뉴런과 1000 학습주기일 때의 0.4115이다. 그 결과 비드 폭은 실측치를 중심으로 예측치가 상당히 정확하게 예측됨을 확인하였다.

Figure 7:

Comparison and analysis of predicted values on bead width (GDBP)

Figure 8:

Bead width error rate histogram (GDBP)

3.3.2 LMBP(Gradient Descent Back-Propagation) 알고리즘

Levenberg-Marquardt 알고리즘은 네트워크의 정확도를 높이기 위해 사용하였다. 가중치와 편견(Bias)은 전이함수에 따라 조정하였다.

$\[ \Delta W={\left(J^{T}J+\mu I\right)}^{-1}{J}^{T}e \]$

(7)

여기서 J는 각 오차의 편차에 대한 야코비안 행렬(Jacobian matrix), μ는 스칼라, e는 오차함수이다. LMBP 알고리즘을 이용하여 신경망의 전반적인 정확도를 향상시키고자 하였다. 학습은 목표 오차값에 도달하거나 최대 Epoch 수가 끝날 때 또는 μ가 최대값에 도달할 때까지 계속되었다. 학습에 사용된 데이터는 수직 V그루브 용접실험 45개의 데이터를 이용하였으며, 학습된 신경회로망을 검증하기 위하여 동일한 조건의 평균 비드 폭을 적용하였다. LMBP 신경회로망은 GDBP 신경회로망과 동일하게 Epoch수가 1000일 때, 목표오차가 10-10까지 훈련을 수행하였다. 신경회로망 학습에 사용된 입력층은 용접실험의 입력변수인 용접전류, 아크전압, 용접속도이며, 출력층은 비드 폭으로 비선형 함수는 Tangential sigmoid 함수를 사용하였으며, 학습 알고리즘은 학습속도가 빠른 Levenberg-Marquardt 알고리즘을 사용하였다.

LMBP 신경회로망의 학습조건을 위한 네트워크 구조 설정은 Table 9에 나타냈으며, Levenberg-Marquardt 근사 함수를 이용한 다양한 신경망의 예측성능은 Table 10에 나타냈다. 다양한 신경망의 RMS오차를 비교·분석한 결과 3-14-2구조의 신경회로망을 토대로 최소 RMS오차는 은닉층에 14개의 뉴런과 1000 학습 주기일 때의 0.1136이다. 따라서 모든 예측 데이터가 허용 가능한 범위 안에 있기 때문에 GMA용접의 공정변수를 예측하는데 이용하였다.

Table 9:

LMBP algorithm parameter and their levels

Table 10:

Result of LMBP algorithm prediction performance

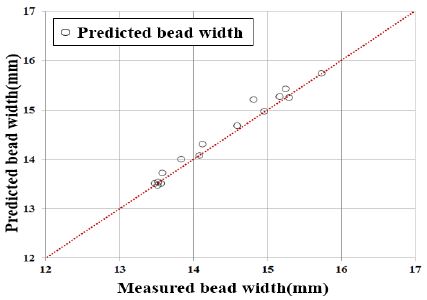
LMBP 신경회로망을 이용하여 예측된 비드 폭과 측정된 비드 폭의 비교 및 그에 따른 오차를 Figure 9와 Figure 10과 같이 나타냈다. 그 결과 비드 폭의 실측치를 중심으로 매우 정확하게 예측함을 확인할 수 있었다.

Figure 9:

Comparison and analysis of predicted values on bead width (LMBP)

Figure 10:

Bead width error rate histogram (LMBP)

3.3.3 PAM 분석을 통한 비드 폭 예측모델 선정

본 연구에서 V그루브의 비드 폭을 예측하고자 2차 회귀방정식, GDBP 및 LMBP 신경회로망을 포함하여 다양한 수학적 모델 및 알고리즘을 개발하였으나, 보다 정확하게 비드 폭 예측성능을 비교·분석하고 용접공정 현장에 즉시 적용시키기 위하여 아래의 식 (8)와 같이 Poliak [14]이 정의한 PAM(Predictive Ability of Model)을 이용하여 정확도를 평가하였다.

$\[ PAM=\frac{N_{PAM}}{N_{total}}\times 100 \]$

(8)

여기서, N_PAM은 $$ \left|\frac{B_M-B_p}{B_M}\right|\le 0.02$$ 범위의 예측치의 수를 나타내며, N_total은 전체 예측치 수를 나타낸다. 그리고 B_M은 실측치 비드 폭이며, B_P는 계산된 비드 폭을 의미한다. PAM은 오차범위 2% 이내에 예측을 정확한 예측으로 간주하여 모델의 정확도를 나타내며, 최대 오차율을 확인함으로써 측정치 비드 폭에 얼마나 근접하게 예측하는지를 나타낸다.

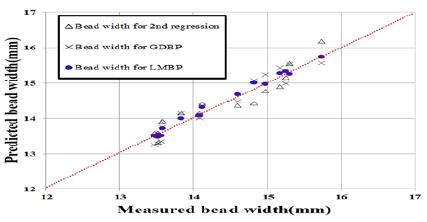
PAM을 이용하여 각 모델별 예측 정확도를 평가한 결과를 Table 11에 나타냈다. PAM 분석결과에 따르면, LMBP 예측모델에서 비드 폭의 최대 오차율은 1.42%로 확인되어 위 모델을 적용할 경우 2% 이내로 비드 폭을 예측 가능할 것으로 판단된다. Figure 11은 각 예측모델에 따른 비드 폭과의 예측치와 실측치를 비교하였으며, 그에 따른 오차율을 비교한 결과, LMBP 신경회로망이 가장 우수한 예측성능을 나타냈다.

Table 11:

PAM analysis of various prediction models

Figure 11:

Comparison and analysis of predicted values on bead width

4. 결 론

본 연구에서는 수직 GMA 용접공정에서 적용되는 V 그루브에 다양한 용접 공정변수에 따른 비드 폭을 제어하기 위한 예측모델을 개발하기 위해 총 15회의 용접실험을 수행하였으며, 광학현미경을 사용하여 비드단면을 측정하였다. 용접시험을 수행함으로써 용접 공정변수와 관련된 2차 회귀방정식, GDBP 및 LMBP 신경회로망을 적용한 3가지 예측모델을 개발하였으며, 정량적으로 성능평가가 가능한 PAM분석을 통해 최적의 비드 폭 예측모델을 선정하였다. 그 결과 GDBP와 LMBP의 신경회로망에서 모두 비드 폭을 PAM 90% 이상으로 정확하게 예측하였지만, 2차 회귀방정식 비드 폭은 직선회귀방정식의 예측성능이 60%로 가장 낮음을 확인하였다. 비교적 학습 데이터의 수가 적고 특히 단순한 신경회로망 구조 및 제한된 실험데이터를 이용하여 신경회로망을 학습한 관계로, 일부 예측값은 2.83%의 오차율이 발생되는 것을 확인하였다. 최대 예측 오차율의 확인을 통해 분석한 결과, LMBP 알고리즘에서 최대 1.42% 오차율을 보여 가장 정밀한 비드 폭을 예측하는 모델로 선정하였으며, Vertical position 용접 자동화 구현에 있어 최적화 알고리즘 및 On-Line 용접품질 시스템에 적용이 가장 적합할 것으로 사료된다.

Acknowledgments

본 연구는 2015년도 정부(교육부)의 재원으로 한국연구재단의 지원을 받아 수행된 기초연구사업임(No.2015R1D1A3A01020246).

References

• G. Doumanidis, M. Hale, and D. E. Hardt, “Multi-variable control of arc welding processes”, Proceeding of International Conference on Trends in Welding Research, p449-457, (1986).
• R. J. Remwick, and R. W. Richardson, “Experimental investigation of GTA weld pool oscillation”, Welding Journal, vol. 62(no. 2), p29-35, (1983).
• P. M. Gonseth, and P. Blanc, “Optiguide - A new optical joint rracking device”, Welding Journal, vol. 62(no. 9), p27-29, (1983).
• S. H. Lee, “Investigation of metal transfer in GMAW using pinch instability theory with arc pressure”, Journal of the Korean Society Precision Engineering, vol. 11(no. 3), p191-196, (1994), (in Korean).
• W. E. Lukens, and R. A. Morris, “Infrared temperature sensing of cooling rates for arc welding control”, Welding Journal, vol. 27(no. 33), (1982).
• Y. Kozono, and S. Kokura, “Relation between surface temperature and reverse side bead width in Girth TIG welding for stainless steel tube”, Quarterly Journal of the Japan Welding Society, vol. 4(no. 2), p331-335, (1986).
• S. A. Haytcher, A. L. Kilty, H. W. Ludewig, D. E. Rees, J. H. Siwicke, and B. L. Wallace, “Method for arc welding fault detection”, US Patent, 5521354, May, 28), (1996.
• T. P. Quinn, C. Smith, C. N. McCowan, E. Blachowiak, and R. B. Madigan, “Arc sensing for defects in constant-voltage gas metal arc welding”, Welding Journal, vol. 78(no. 9), p322-328, (1999).
• S. Adolfsson, A. Bahrami, G. Bolmsjo, and I. Claesson, “On-line quality monitoring in shortcircuit gas metal arc welding”, Welding Journal, vol. 78(no. 2), p59-73, (1999).
• J. Raveendra, and R. S. armar, “Mathematical models to predict weld bead geometry for flux cored arc welding”, Journal of Metal Construction, vol. 19(no. 2), p31-35, (1987).
• R. S. Chandel, “Mathematical modeling of gas metal arc weld features”, Proceedings of the 4th International Conference on Modeling of Casting and Welding Processes, vol. 17(no. 22), p109-120, (1988).
• I. S. Kim, C. E. Park, Y. H. Cha, B. S. Seong, Y. M. Park, Y. H. Ahn, K. W. Kim, and Y. J. Jeong, “Selection of optimal process parameters for butt welding”, The Korean Welding and Joining Society, vol. 2, p3-6, (2001), (in Korean).
• D. S. Kim, and Y. S. Park, “Optimization of electro- UV-ultrasonic complex process for E. coli disinfection using box-Behnken experiment”, Korean Society Of Environmental Engineers, vol. 33(no. 3), p149-156, (2011). [https://doi.org/10.4491/ksee.2011.33.3.149]
• E. I. Poliak, “Application of linear regression analysis in accuracy assessment of rolling force calculations”, Metals and Materials, vol. 4(no. 5), p1047-1056, (1998). [https://doi.org/10.1007/bf03025975]