건조단계 잠수함 품질정보 기반의 함 탑재장비 신뢰성 분석 및 활용방안

2.1 잠수함별 탑재장비 고장발생 비율

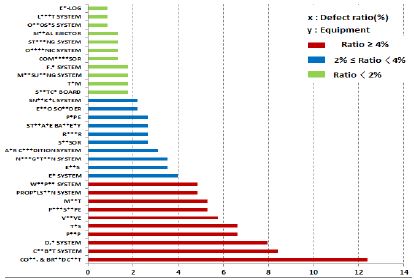
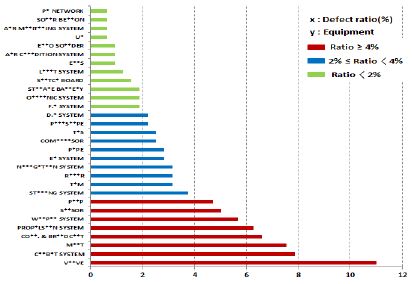
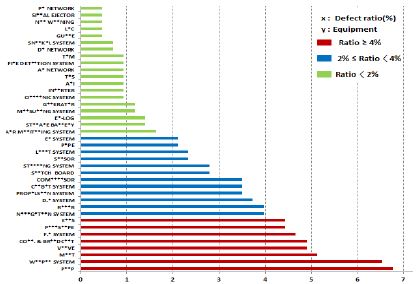
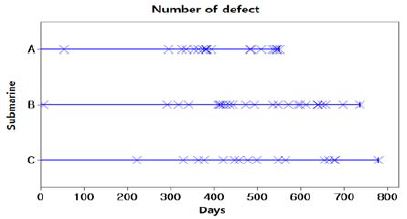
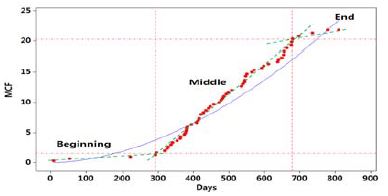
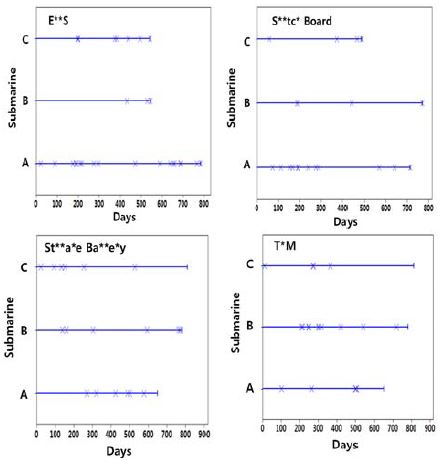
조선소에서 건조한 잠수함은 탑재장비 설치상태 검사, 공장수락시험, 입고검사, 정박 시운전 및 항해 시운전을 통해 각 탑재장비들에 대한 엄격하고 정확한 성능평가를 거쳐 해군으로 인도된다. 국방기술품질원 및 해군 인수평가대는 각 시험 및 시운전 단계에서 발생한 고장에 대해 시정조치 요구 및 조치 후 결과 확인으로 탑재장비의 정상작동 및 고장 수리상태를 확인하고 있다. 본 연구에서는 함 건조단계에서 발생한 시정조치 요구 및 탑재장비 관련 이슈사항을 품질정보로 환류하여 건조단계 잠수함 3척에 대한 탑재장비 품질정보를 획득하였다. 여기서 품질정보는 각 탑재장비에 대한 고장발생 건수, 고장발생 시점, 그리고 국방기술품질원, 해군 및 조선소 등 각 기관별로 관리한 고장정보의 통합 집계를 의미한다. 먼저 다빈도 고장발생 탑재장비를 파악하기 위해 고장발생 시점을 고려하지 않고 건조시작 시점부터 건조완료 시점까지 각 잠수함의 탑재장비에 대한 고장발생 비율을 분석하였다. Figure 1, Figure 2 및 Figure 3은 건조단계 잠수함 3척에서 각각 획득한 탑재장비 고장발생 비율이며, 각 잠수함에서 발생한 전체 고장건수를 기준으로 하여 나타내었다. 이때, 고장이 1건 이하로 발생한 탑재장비는 제외하고 세 그룹으로 구분하였으며, 실적함 건조 중 고장으로 인해 공정에 미쳤던 영향의 경중을 고려하여 고장발생 비율 단계는 2% 및 4%를 기준으로 설정하였다. 붉은색은 전체 고장발생 비율 중 4% 이상을 차지하는 탑재장비를 나타내며, 푸른색은 2% 이상 4% 미만을 차지하는 탑재장비를 나타내며, 초록색은 2% 미만을 차지하는 탑재장비를 나타낸다. 품질정보 기반의 비교분석을 통해 수십 종의 탑재장비 중 3척에서 공통적으로 다수의 고장이 발생한 탑재장비를 파악하였다. 각각의 잠수함을 건조한 조선소가 다르며 3척의 잠수함 건조가 동시에 이루어지지 않고 기간의 차이를 두고 병렬적으로 건조된 점을 고려할 때, 각 잠수함에서의 개별 탑재장비에 대한 고장발생 비율은 정확하게 일치하지 않았으나, 고장발생 경향성 확인 및 고장발생 비율 비교를 통해 다빈도 고장발생 탑재장비를 선정하였다.

Figure 1:

Equipment defect ratio for A submarine

Figure 2:

Equipment defect ratio for B submarine

Figure 3:

Equipment defect ratio for C submarine

2.2 다빈도 고장발생 탑재장비 선정

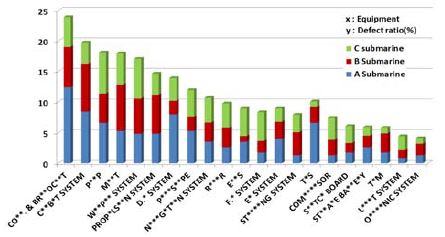
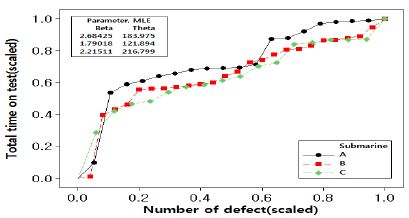
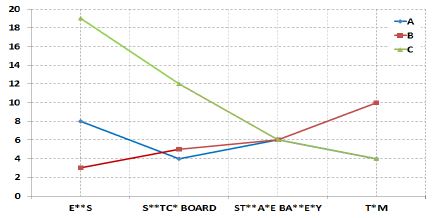
본 연구는 수많은 잠수함 탑재장비 중 건조단계에서 공통적으로 다수의 고장이 발생한 탑재장비에 대한 신뢰성 분석이 목적이므로 다빈도 고장발생 탑재장비 식별이 선행되어야 한다. 건조단계 잠수함 3척에 대한 품질정보를 통합하여 고장발생 건수 순으로 나열한 후 고장발생 비율이 1% 이상인 21종의 탑재장비를 신뢰성 분석 대상으로 선정하였다. Figure 4는 선정된 탑재장비가 각 잠수함에서 차지하고 있는 고장발생 비율을 나타낸다. 가로축은 3척의 잠수함 품질정보를 통합하여 장비 고장발생 건수 순으로 나열하였고 세로축은 각 잠수함별 고장발생 비율로 도시하고 있다. 3척의 잠수함을 통합하여 고려했을 때와 각 잠수함별로 고려했을 때 탑재장비에 대한 가로축의 순서와 세로축 지시값의 순서가 일치하지 않지만, 비슷한 경향을 나타내는 것을 확인할 수 있다.

Figure 4:

High proportion of defect for equipments(21EA)

Table 1은 선정된 다빈도 고장발생 탑재장비에 대한 각 잠수함별 고장비율과 3척의 잠수함을 하나의 시스템으로 통합하였을 때 산출되는 고장비율을 나타낸다. 21종의 탑재장비를 살펴보면 잠수함 통신 및 방송관련 장비 1종, 항해레이더, 항해체계, 타기조종 계통 등 항해관련 장비 5종, 어뢰발사관, 어뢰기만기, 선배열 예인소나, 전자전 장비 등 전투체계 관련 장비 5종, 디젤엔진, 추진체계, 마스트, 펌프류 등 추기 및 기장관련 장비 5종, 축전지, 배전반, 연료전지, 조명계통 등 전기관련 장비 5종으로 구성되어 있다. 이때, V**ve의 경우 3척에서 공통적으로 4% 이상의 고장발생 비율을 보이고 있으나, 유압으로 구동되는 탑재장비의 시스템에 모두 포함되는 장비로써 특정 탑재장비에 대한 고장발생 경향을 나타내지 않으므로 제외하였다.

Table 1:

Defect ratio of equipments for A, B, C and Integration (ABC : A + B + C) (unit : %)

3.1 모수적 신뢰성 분석 기법

수리 가능한 시스템에서 고장에 따른 수리나 교체는 고장발생 직전과 동일 조건으로 회복시키는 최소수리를 가정한다. 이때, 최소수리는 NHPP(Non-homogeneous Poisson Process) 모형으로써 수리 가능한 시스템에 대한 고장을 모형화 할 수 있다[3]. NHPP 모형은 일정하지 않은 고장발생률(ROCOF:Rate of Occurrence of Failure)을 가지는 포아송 과정이다[4]. 수리 가능한 시스템의 고장발생률 모형은 주로 Crow가 제안한 PLP(Power Law Process)가 많이 사용된다[5]. PLP 모형은 (0,t]에서 고장발생률 λ(t)를 식 (1)과 같이 나타낼 수 있는 멱함수 NHPP 모형이며, 이에 상응하는 평균누적함수(MCF:Mean Cumulative Function) μ(t)는 식 (2)와 같이 나타낼 수 있다.

여기서, β는 형상모수, θ는 척도모수, t는 고장발생 시간이다. MCF는 임의의 시점에서 각 개체들의 고장발생 누적함수를 평균한 값들의 집합이다. 즉, MCF의 세로축은 특정 시점에서 고장수의 평균값을 의미하므로 MCF의 세로축 지시값을 통해 해당 시점에서의 탑재장비 고장소요 추정이 가능하다[6]. 수리 가능한 시스템에서 모수적 추정방법을 이용한 신뢰성 분석이 가능한 경우는 멱함수 NHPP 모형이므로 이에 대한 추세검정이 필요하다. 추세검정 방법으로는 Laplace 검정, Anderson-Darling 검정, MIL-HDBK-189 검정 등이 있으나, 주로 Laplace 검정의 경우 대수선형 NHPP 검정에 사용되며, Anderson-Darling 검정의 경우 HPP(Homogeneous Poisson Process) 검정에 사용되며, MIL-HDBK-189 검정의 경우 멱함수 NHPP 검정에 사용된다. 따라서 MIL-HDBK-189 검정을 이용하여 3척의 잠수함에서 다빈도 고장발생 탑재장비 고장모형에 대한 멱함수 NHPP 모형 적용 적정성 분석 및 이에 대한 추세검정이 필요하다[4].

3.2 멱함수 NHPP 고장모형 탑재장비

탑재장비 고장발생 모형에 대한 멱함수 NHPP 모형 적용 적정성 분석을 위해 수행된 MIL-HDBK-189 검정결과이다. 이때, 귀무가설 및 대립가설은 다음과 같다.

귀무가설(H₀) : 고장발생이 일정한 HPP이다.
대립가설(H₁) : 고장발생이 일정하지 않은 NHPP이다.

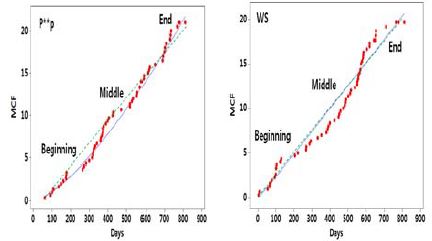
여기서 HPP는 형상모수 β = 1을 의미하며, NHPP는 형상모수 β≠1을 의미한다. 귀무가설을 기각하는 조건은 또는 $$ 2n/\widehat{\beta }>{\widehat{\chi }}_{1-\alpha /2}\left(2n\right)$$ 이다[7]. 여기서 n은 관측된 총 고장발생 건수, $$ \widehat{\beta }$$은 형상모수의 모수 추정값, $$ \widehat{\chi }$$는 MIL-HDBK-189 검정통계량, α는 유의수준이다. 이때, 각각의 잠수함을 건조하는 조선소가 다르고 건조하는 시점이 다르며, 탑재장비의 고장발생은 해당 장비뿐만 아니라 타 장비와의 복잡한 연동문제로 인해 발생하기도 하므로 해당 탑재장비의 운용시간을 기준으로 하여 고장자료를 실시간으로 수집하기 곤란하다. 따라서 운용단계가 아닌 건조단계에서 발생한 고장이라는 특성을 반영하여 품질정보 관리 및 이에 대한 분석은 일(days) 단위로 수행하였다. Table 2는 멱함수 NHPP 고장모형을 따르는 탑재장비에 대한 각 잠수함에서의 MIL-HDBK-189 검정통계량 및 우도비 카이제곱 검정에 따른 P-value를 나타낸다. 선정된 21종의 탑재장비 중 MIL-HDBK-189 검정에 따라 멱함수 NHPP 모형을 따르는 탑재장비는 C**b*t System, M**t, P***s**pe, R***r, T*S 등 15종임을 확인하였다. 3척의 경우 모두 이므로 귀무가설을 기각하고 고장발생 모형이 멱함수 NHPP를 따른다고 할 수 있다. 아울러, 각 잠수함에서의 탑재장비 고장발생 모형 동질성 검정을 위한 우도비 카이제곱 검정에 따른 P-value가 0.05보다 훨씬 크므로 서로 형상모수가 유의하게 다르다고 할 수 없으며, 3척에 대한 각각의 탑재장비 고장발생 모형을 통합하여 분석 가능함을 강력하게 보여주고 있다. 다음은 상기 탑재장비 중 대표적으로 C**b*t System에 대해 모수적 추정방법을 이용하여 신뢰성 분석을 수행한 결과이다. Figure 5는 A함, B함, C함 각각에서 발생한 C**b*t System 고장발생 빈도 및 간격을 나타낸다. Figure 6은 각 잠수함의 C**b*t System 고장발생에 대한 TTT-plot이다. TTT-plot은 Barlow & Campo(1975)에 의해 소개된 추세검정 도시방법으로써 타점된 값들이 45° 직선상에 위치하면 추세가 없는 HPP 모형이라고 판단할 수 있고, 45° 직선상에 위치하지 않으면 NHPP 모형이라고 판단할 수 있다. 3척 모두 β>1 임을 확인할 수 있고, 위로 볼록한 형태이므로 고장발생률 λ(t)가 증가하고 있음을 알 수 있다[3]. 이것은 잠수함이 해군에 인도되기까지 정해진 기간 내에 많은 양의 시운전 평가를 거침에 따라 나타나는 결과로 판단된다. 인도 후 탑재장비에 대한 품질문제가 발생할 경우, 보증수리를 통해 각 탑재장비에 대한 품질 안정화를 달성하고 있다.

Table 2:

Test statistics for MIL-HDBK-189 on each submarine

Figure 5:

Number of defect for C**b*t System

Figure 6:

TTT-plot for C**b*t System on each submarine

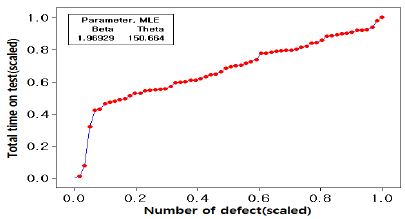
Figure 7은 3척의 잠수함에 대한 C**b*t System 고장발생 모형을 통합하여 나타낸 TTT-plot이다. β가 1.96929로 β>1 임을 확인할 수 있으며, 3척의 잠수함을 통합하여 산출된 고장발생률 λ(t) 역시 증가하고 있음을 알 수 있다.

Figure 7:

TTT-plot for C**b*t System on ABC

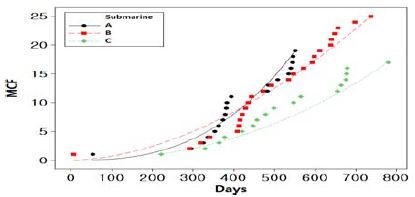
Figure 8은 각 잠수함의 C**b*t System 고장발생에 대한 MCF이다. 이때, A함, B함, C함은 조선소 및 건조공정의 차이로 시간 관측중단 시점이 각각 650, 780, 810일로 상이하다. Figure 9는 3척의 잠수함을 통합하여 나타낸 C**b*t System 고장발생 MCF이다.

Figure 8:

MCF for C**b*t System on each submarine

Figure 9:

9: MCF for C**b*t System on ABC

각 탑재장비에 대해 MCF가 급변하는 시점별로 구간을 나누어 구간별 회귀분석을 수행하였으며, 그 결과를 Table 3, Table 4 및 Table 5에 나타내었다. 이때, P-value를 살펴보면 각 탑재장비에 대한 각 구간별 직선 회귀식은 유의수준 0.05에서 매우 유의하다고 할 수 있다. MCF 기울기는 단위 관측시간당 누적 고장발생 변화를 나타내는 비율이다. 고장발생 모형 전체 구간에 대한 고장발생률은 일정하지 않지만, 분석대상 구간에서 MCF 기울기가 직선으로 표현되면 고장발생률이 일정한 포아송 과정으로 해석할 수 있다. 따라서 MCF의 기울기 역수를 통해 MTBF(Mean Time Between Failure)를 추정할 수 있으며, MCF 기울기 변화 추적을 통해 고장발생 변화 추이를 확인할 수 있다[6].

Table 3:

R2 and ANOVA for MCF regression equation I (1st : Beginning period / 2nd : Middle period / 3rd : End of period)

Table 4:

R2 and ANOVA for MCF regression equation II (1st : Beginning period / 2nd : Middle period / 3rd : End of period)

Table 5:

R2 and ANOVA for MCF regression equation III (1st : Beginning period / 2nd : Middle period / 3rd : End of period)

건조 초기단계인 공장수락시험, 입고검사, 설치상태 검사 단계에서는 각 탑재장비가 타 장비들과 연동하여 실 작동 하기 전 이므로 MCF 기울기가 타 구간에 비해 상대적으로 완만한 것을 확인할 수 있다. 건조 중기단계라고 할 수 있는 정박 시운전 및 항해 시운전 단계에서는 타 탑재장비들과의 연동상태, 장비 작동상태 및 함 운용 성능을 확인한다. 이때, 탑재장비 구성부품 불량, 연동 불량, 절연 불량, 수밀 불량, 탑재장비 내부 S/W 문제 등 다양한 원인들로 인한 탑재장비 고장이 식별된다. 따라서 Figure 9와 같이 MCF 기울기가 타 단계에 비해 급하며, 붉은 타점이 몰려 있는 것으로 보아 고장발생 빈도 역시 잦은 것을 확인할 수 있다. 잠수함 인도 시점에 가까운 건조 말기단계에서는 다양한 종목의 정박 시운전 및 항해 시운전을 통해 각 탑재장비의 성능 안정화가 달성 되었으므로, 건조 초기단계와 같이 MCF 기울기가 다시 완만해지는 것을 알 수 있다. 단, 관측기간이 타 단계보다 짧으므로 MCF 기울기의 절대값은 건조 중기단계보다 큰 값을 보인다. C**b*t System 외 나머지 14종의 탑재장비 역시 대부분 비슷한 경향을 나타낸다. 정박 및 항해 시운전 단계에서 고장이 가장 많이 식별되며, 이후 품질 안정화 과정을 거친다. 그러나, 각 장비 특성 및 시운전 수행 시점이 다르므로 각 장비별 MTBF를 추정하여 이에 대한 품질관리가 필요하다. 대표적으로 C**b*t System의 MTBF는 건조 초기단계에서 중기단계 사이가 73.85일, 건조 중기단계에서 말기단계 사이가 28.28일, 건조 말기단계에서 전력화 시점 사이가 20.47일로 추정된다. 여기서 건조 말기단계의 MTBF가 건조 중기단계보다 짧게 추정되는 것은 건조 말기단계의 관측기간이 건조 중기단계에 비해 상대적으로 많이 짧기 때문이다.

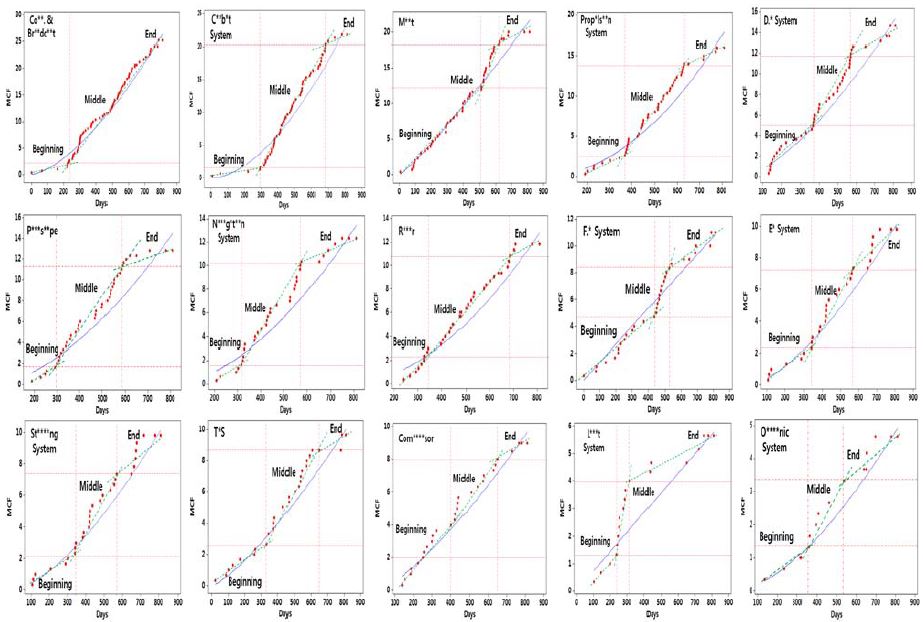
Figure 10은 멱함수 NHPP 고장모형을 따르는 탑재장비 15종 각각에 대해 3척의 잠수함을 통합하여 나타낸 MCF이며, Table 3, Table 4 및 Table 5에 따라 MCF가 급변하는 시점별로 구간을 나누어 직선 회귀식을 녹색으로 도시하였다. 이때, R2과 분산분석을 통한 P-value를 통해 산출된 직선 회귀식이 타당함을 검증하였다.

Figure 10:

MCF for equipments of power function NHPP failure model(15EA) on ABC

3.3 HPP 고장모형 탑재장비

Table 6은 고장발생 모형이 멱함수 NHPP 모형을 따르지 않고 HPP 모형을 따르는 탑재장비에 대해 각 잠수함에서의 MIL-HDBK-189 검정통계량 및 우도비 카이제곱 검정에 따른 P-value를 나타낸다. 선정된 21종의 탑재장비 중 MIL-HDBK-189 검정에 따라 유의수준 0.05에서 HPP 모형을 따르는 탑재장비는 P**p, W**p** System(이하 WS)임을 검정을 통해 확인하였다. 아울러, 각 잠수함에서의 탑재장비 고장발생 모형 동질성 검정을 위한 우도비 카이제곱 검정에 따른 P-value가 0.05보다 훨씬 크므로 3척의 잠수함 각각의 탑재장비 고장발생 모형을 통합하여 분석할 수 있다.

Table 6:

Test statistics for MIL-HDBK-189 on each submarine

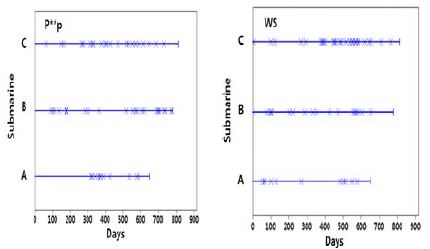
다음은 P**p 및 WS에 대한 신뢰성 분석 결과이다. Figure 11은 A함, B함, C함 각각에서 발생한 P**p 및 WS 고장발생 빈도 및 간격을 나타내며, Figure 12는 3척의 잠수함에 대한 탑재장비 고장발생 모형을 통합하여 나타낸 TTT-plot이다.

Figure 11:

Number of defect for P**p and WS

Figure 12:

TTT-plot for P**p and WS on ABC

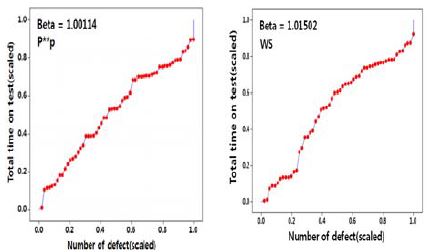
β가 각각 1.00114, 1.01502≈1 이며, TTT-plot상의 타점된 값들이 거의 45° 직선상에 위치하고 있으므로 고장발생률 λ(t)는 추세가 없다고 판단할 수 있다. 아울러, Figure 13은3척의 잠수함을 통합하여 나타낸 P**p 및 WS 고장발생 MCF이며, 이에 대한 회귀분석 결과는 Table 7과 같다.

Figure 13:

13: MCF for P**p and WS on ABC

Table 7:

R2 and ANOVA for MCF regression equation

3척의 잠수함에 대한 탑재장비 고장발생 모형을 HPP 모형으로 통합하였을 때 산출되는 MTBF는 P**p 34.53일, WS 39.12일이다. Figure 11과 같이 각 잠수함에서 P**p 및 WS의 고장발생 빈도 및 간격은 상이하나, 하나의 HPP 모형으로 통합하여 MTBF를 산출함으로써 건조 초기단계, 중기단계 및 말기단계에 걸쳐 해당 장비가 평균적으로 고장이 발생할 수 있는 간격을 제시하였다.

3.4 멱함수 NHPP 및 HPP 혼합 고장모형 탑재장비

Table 8은 고장발생 모형이 멱함수 NHPP 모형 및 HPP 모형이 혼재하는 탑재장비에 대한 MIL-HDBK-189 검정통계량 및 고장발생 모형을 나타낸다. 고장발생 모형의 혼재로 3척의 잠수함 품질정보를 통합할 수 없으므로 해당 탑재장비에 대한 정략적 MTBF를 제시하기는 어렵다. 따라서 Figure 14및 Figure 15와 같이 A함, B함, C함 각각에서의 해당 탑재장비에 대한 고장발생 빈도 및 간격을 분리하여 나타냈다. 선정된 다빈도 고장발생 탑재장비 21종 중 상대적으로 고장발생 빈도가 낮은 장비에서 멱함수 NHPP 모형 및 HPP 모형이 혼재하는 경우가 관측되었다. 이것은 고장발생 모형을 분석하는데 품질정보가 충분하지 않다는 것을 의미할 수 있으며, 좀 더 세밀한 분석을 위해서는 3척의 잠수함 이후 건조되는 후속함에 대한 품질정보를 본 연구에 환류하여 신뢰성 분석이 추가적으로 이루어져야 할 것으로 판단된다.

Table 8:

Test statistics for MIL-HDBK-189 on each submarine

Figure 14:

Number of defect for NHPP & HPP mixed type

Figure 15:

Defect plot for NHPP & HPP mixed type

3.5 야전운용 데이터 신뢰성 분석결과 비교

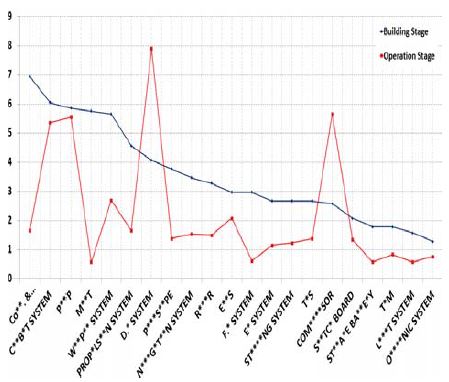
본 논문의 신뢰성 분석대상과 동일한 현재 작전 운용중인 잠수함 3척의 탑재장비에 대한 야전운용 데이터를 이용하여 건조단계 다빈도 고장발생 탑재장비와 비교분석을 수행하였다. 야전운용 데이터는 ‘07년도에서 ‘16년도까지 총 10년간 수집된 잠수함 탑재장비에 대한 고장발생 관련 정보이다[2]. 야전운용 데이터를 통해 산출된 각 탑재장비에 대한 MTBF 구체적 수치는 군사자료이며, 실제 장비운용 누적시간을 기준으로 산출되었으므로 본 논문을 통해 추정된 건조단계 탑재장비 MTBF와 직접적인 비교는 어려우나, 건조단계에서의 탑재장비 고장발생 비율과 야전운용 단계에서의 탑재장비 고장발생 비율 비교를 통해 고장발생 경향성을 살펴보았다. Figure 16은 건조단계와 야전운용 단계에서 탑재장비에 대한 고장발생 비율을 비교하여 나타냈다.

Figure 16:

Compare with Building stage and Operation stage

건조단계의 경우 21종의 탑재장비가 총 고장발생 건수 의 74.6%를 차지하는 반면, 야전운용 단계의 경우 해당 탑재장비가 총 고장발생 건수의 46.1%를 차지하였다. 이는 오랜 시간동안 함 운용 과정을 거치면서 건조단계에서는 문제되지 않았던 장비들의 고장이 증가함에 따라 21종의 탑재장비 고장건수 비율이 상대적으로 감소한 결과로 판단된다.

그러나, 건조단계와 야전운용 단계에서 고장발생 비율 및 빈도의 경향은 차이가 있었지만, 건조단계에서 고장이 다빈도로 발생한 탑재장비는 야전운용 단계에서도 고장이 잦은 것을 확인할 수 있으므로 상기 탑재장비에 대해서는 건조단계 뿐만 아니라 야전운용 단계에서도 꾸준한 품질관리가 요구된다.