도플러 천이/도달지연시간차 하이브리드 기법을 이용한 수중 고속 기동 표적의 속도 및 거리 추정 기법

1. 서 론

수중에서 기동하는 표적의 속도와 거리를 측정하는 기법은 민간이나 군사적으로 매우 많이 활용되고 있으며, 정확도를 향상시키기 위한 다양한 탐지 기법이 연구되고 있다[1][2].

최근에는 측정 장비의 시간 측정정확도 성능 향상으로 인해 특정 음파를 송신하지 않고 선배열 센서로 수신되는 표적의 방사소음 도달지연시간차(TDoA)를 이용하여 표적의 위치를 측정하는 기법이 많이 연구 되었다[3]. 이때, TDoA 성능에 결정적인 영향을 미치는 요소는 선배열 센서의 간격 및 표적의 속도 그리고 센서로 부터의 거리이다[4].

M. S. Han et al. [4]는 표적이 센서로부터 근접 고속 기동할 경우 TDoA 기법 적용시 복합 수중 채널의 영향을 최소화 하여 수신신호의 상관도를 최대로 할 수 있는 최적의 센서 간격에 대한 연구를 수행하였으며, 분석 주파수 대비 4λ이하의 센서 간격을 제시하였다. 하지만 수신되는 신호의 상관도를 높이기 위해 선배열 센서 간격을 너무 좁게 할 경우 TDoA 기법 적용시 미세한 방위 오차가 포함되더라도 큰 거리 추정오차를 야기할 수 있다. 특히, 표적 장비의 RPM (Revolution Per Minute) 정보는 불가피하게 시간적으로 변하기 때문에 표적 수중방사소음을 이용하는 TDoA 성능은 더욱 저하된다. 그러므로 근접 고속 기동하는 표적의 속도 및 거리 추정 정확도 향상을 할 수 있는 별도의 기법이 추가로 요구된다.

도플러 천이(doppler shift) 기법은 표적이 일정한 궤적과 속력으로 CPA 통과시 변화하는 기계류 소음원의 협대역 주파수 변화량을 관찰 및 이용하는 기법이다[5]-[7]. 이때, 특정 시점에서의 도플러 주파수의 최대 및 최솟값 변화량을 측정하면, 표적의 속도 정보를 계산할 수 있다[8]. 하지만 S. Barnwal et al. [8]은 도플러 기법 수식에 표적의 방위각 정보 cosθ를 1로 가정했기 때문에 방위각에 따른 속도 정보 오차가 존재한다.

따라서 본 논문은 도플러 천이 및 TDoA 하이브리드 기법을 이용하여 수중에서 선배열 센서로부터 근접 고속 기동하는 표적의 파라미터를 추정하는 기법을 제시한다. 우선 표적이 CPA 통과시 특정 시점에서의 수신기와 표적의 상대 속도에 의해 발생되는 도플러 주파수 최대 및 최소값을 계측한다. 다음으로 TDoA 기법을 이용하여 도플러 주파수 계측 시점에서의 표적 방위각을 계산하고 도플러 기법 수식에 대입함으로써 표적의 속도를 계산한다. 그리고 계산된 속도 정보를 삼각함수 기법에 적용하여 CPA 시점에서의 거리를 계산한다. 최종적으로 제안된 기법의 성능 검증을 위해 해상실험을 수행하였다.

2. 제안 방법

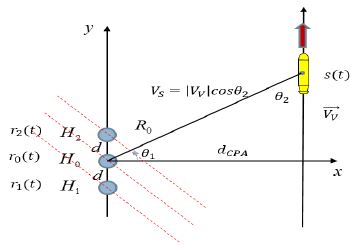
일정한 속도로 기동하는 표적에서 방사되는 소음 s(t)는 Figure 1과 같이 선배열 센서에 r_n(t)으로 수신되고 n은 센서들의 번호이다.

Figure 1:

Target moving at a constant velocity on a straight path

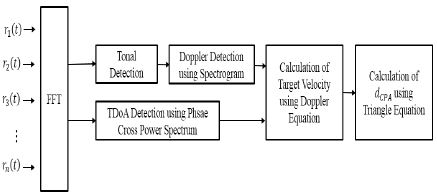
Figure 1에서 R₀ 및 θ₁ 그리고 V_S는 H₀ 센서에서 바라보는 표적의 거리 및 방위 그리고 상대속도를 나타낸다. 그리고 |V_V|는 일정한 속도로 기동하는 표적의 진속도이며, d_CPA는 표적과 H₀ 센서간의 CPA 거리를 나타낸다. 이때 수신되는 표적의 방사소음은 선배열 센서 간격에 따라 서로 다른 위상정보를 갖고 도달하고 이 정보를 이용해 각 신호의 TDoA를 계산할 수 있다. 또한 표적이 H₀ 센서를 기준으로 CPA를 통과하게 되면 표적의 엔진 또는 기계류 방사소음의 주파수가 도플러 천이 현상에 의해 변화된다. 이러한 정보를 이용하여 표적의 진속도 |V_V| 및 R₀ 그리고 d_CPA를 추정하기 위해 제안된 알고리즘은 Figure 2와 같다.

제안된 알고리즘은 CPA 상황에서 수신된 신호 r_n(t)를 FFT한 후 도플러 주파수 및 방위 탐지를 실시하고 계산된 결과 값을 doppler shift/TDoA 하이브리드 기법에 적용함으로써 표적의 속도 및 거리를 계산한다.

Figure 2:

Proposed algorithm for estimation of target’s velocity and distance

2.1 표적 도플러 탐지

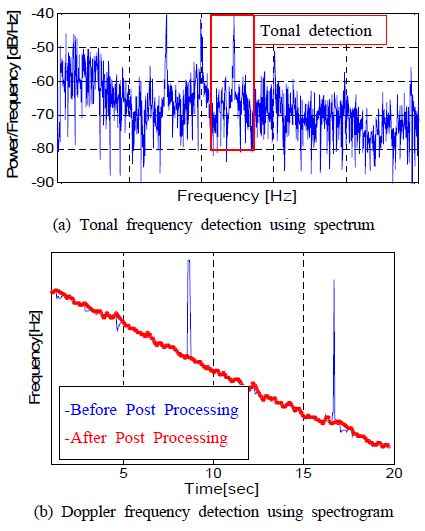
CPA 상황에서 표적 방사소음에 대한 주파수 변화량을 측정하기 위해 Figure 3과 같이 H₀ 센서를 기준으로 배경소음 대비 표적 방사소음 신호의 세기가 특정 값 이상의 주파수를 탐지한다.

Figure 3:

Target doppler frequency detection from H0 sensor

Figure 3 (a)는 표적 방사소음의 1초간의 스펙트럼 결과이며, 특정 토널 주파수를 탐지한다. 이때, 탐지된 토널 주파수는 표적 장비 및 해상 상태에 따라 왜곡될 수 있으므로 탐지 결과에 kalman filter 및 보간법 등을 적용하여 시간에 따라 Post processing을 수행한 후 Figure 3 (b)와 같이 나타낸다[9].

2.4 표적 CPA 거리 추정

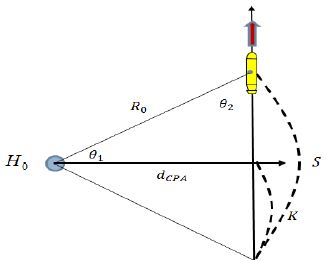
H₀센서를 기준으로 표적이 일정 시간동안 등속도 |V_V|로 Figure 4와 같이 기동 할 때 표적과 센서간의 상대거리 R₀ 및 d_CPA는 식 (11) ~ 식 (14)와 같다.

Figure 4:

Geometrical view of calculating target distance

표적의 이동거리 S는 식 (11)과 같이 표적 이동시간 t와 속도 |V_V|와의 곱과 같다.

$\[ S=\left|V_V\right|\times t \]$

(11)

Figure 5에서 표적의 총 이동거리의 S의 절반인 K는 표적이 등속도 기동을 하였기 때문에 식 (12)와 같다.

Figure 5:

Sound Velocity Profile

$\[ K=S/2 \]$

(12)

여기서 H₀ 센서에서 바라보는 표적의 대각선 거리 R₀는 식 (13)과 같으며, θ₂와 K로 나타낼 수 있다.

$\[ R_0=\frac{S}{2\times \text{cos}{\theta }_2} \]$

(13)

최종적으로 d_CPA값은 삼각함수 공식을 사용하여 식 (14)와 같이 나타낸다.

$\[ d_{CPA}=\sqrt{R_0^2-K^2} \]$

(14)

3. 해상실험 및 결과

3.1 해상실험 환경

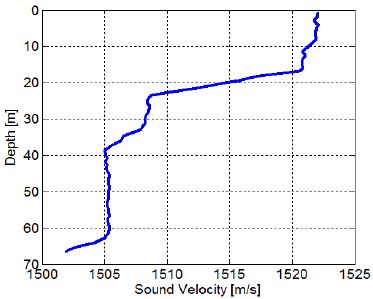
본 실험은 남형제도 근방에서 수행하였으며, 해역의 수심은 약 70m 천해이다. 시험 당시 해양환경은 SS(Sea State) 2정도였으며, Bathythermograph로 측정된 수심에 따른 수중음속은 Figure 5과 같다.

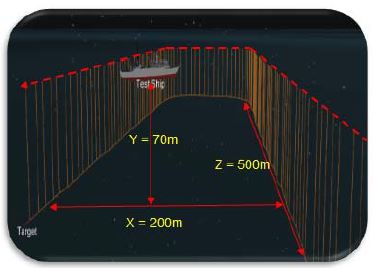
Figure 6은 표적의 관성항법장치 데이터를 기초로 실제 해상실험 진행을 도식화 한 것이며, 시험선 CPA 기준 25노트의 속도로 x축 200m, y축 70m, z축 500m 왕복 기동 하였다.

Figure 6:

Geometrical view of target tracks in sea trial

표적 수중방사소음 수신 및 속도 그리고 거리 계산 하고 근접 고속 기동하는 표적의 TDoA 성능 향상을 위해 M. S. Han et al. [4]이 제안한 바와 같이 시험선 우현 측에 Figure 7처럼 3개의 센서를 분석주파수 대비 4λ 간격으로 설치 하였으며, 사용된 장비 사양 및 정보는 Table 1과 같다.

Figure 7:

Sensors arrangement for localization of target

Table 1:

Parameters for experimental equipments

3.2 해상실험 결과

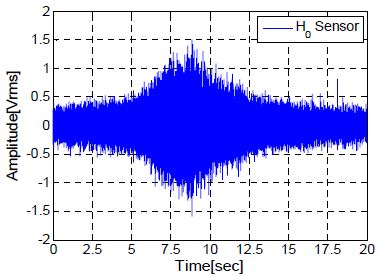
CPA 지점에서의 표적 속도 및 거리 측정을 위해 CPA 기준 ±10초 구간 데이터를 사용하였으며, 이때 수신된 신호는 Figure 8와 같다.

Figure 8:

Received signal from H0 sensor

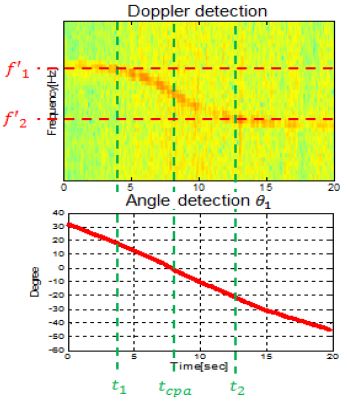
Figure 8에서 CPA 예상 지점인 7~9초 부근 수신음압의 포락선 값이 가장 높게 확인되었다. 이때, 표적의 도플러 및 방위를 계산하기 위해 2장에서 제시한 수식을 적용한 결과는 Figure 9과 같다.

Figure 9:

Result of estimating doppler shift and angle of the target from H0 sensor

Figure 9에서 도플러 탐지시 표적의 기동으로 인하여 특정 대역에서 주파수 천이 현상을 확인할 수 있고 특정 t₁, t₂시점에서의 f′₁ 및 f′₂ 값은 보안과 관련된 이유로 생략한다. 그리고 t₁, t₂ 시점에서 H₀ 센서에서 바라보는 표적의 방위각 θ₁값은 20.10°로 확인되며, 식 (6)에 따라 θ₂는 69.90°이다.

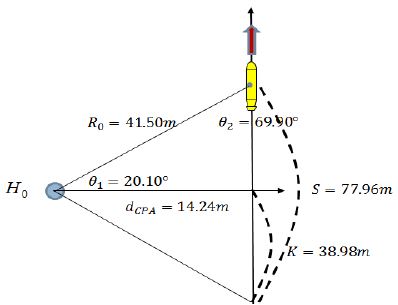
위에서 계산된 값을 식 (10)에 대입하면, 진속도 |V_V|는 25.48 노트로 계산되고 표적의 거리 d_CPA는 Figure 4와 식 (14)에 따라 14.24m로 Figure 10과 같다.

Figure 10:

CPA distance of the target from H0 sensor

제시한 방식과 동일하게 총 6회 해상실험을 진행한 결과를 INS 데이터와 비교한 값은 Table 2와 같다.

Table 2에서 6회 실험에 대한 INS 데이터와 제안된 방법은 속도 편차는 0.78 노트, 거리 편차는 11.61m가 발생하였다.

Table 2:

Performance comparison INS and proposed method

4. 결 론

수중에서 기동하는 표적의 속도 및 거리를 측정하기 위해 표적에서 방사되는 기계류 소음을 이용하는 TDoA 기법이 연구되어 왔다. 하지만 표적이 측정 선배열 센서로부터 근접 고속으로 기동할 경우 수신되는 방사소음이 복합 수중 채널 영향을 받아 왜곡되어 수신 신호들 간의 상관도 성능을 급격하게 저하시킨다. 따라서 선배열 센서 간격을 4λ이하로 좁게 만들었지만 TDoA 기법 특성상 센서간 간격이 좁으면 조금의 방위각 오차에도 큰 거리 오차로 야기 될 수 있다.

본 논문에서는 기존의 TDoA 기법의 한계를 극복하기 위해 표적이 CPA 지점을 지날 때 특정 시점에서 발생되는 도플러 주파수 변화량 및 방위각을 관측하여 도플러 방정식에 대입함으로써 표적의 속도 및 거리를 측정 하는 방법을 제안하였다. 그리고 제안된 방법 검증을 위해 6번의 해상실험을 실시한 결과 INS 데이터 기준 속도 편차는 0.78 노트, 거리 편차는 11.61m가 발생하였다. 하지만 INS 데이터도 절대적인 값이 아니기 때문에 정확한 비교는 될 수 없지만 표적 기준속력 25노트 대비 약 5% 이내의 정밀도를 가지는 것으로 보아 제안된 기법의 유용성을 잘 보여주고 있다.

References

• C. H. Knapp, and G. C. Carter, “The generalized correlation method for estimation of time delay”, IEEE Transactions on Acoustics, Speech and Signal processing, vol. 24(no. 4), p320-327, (1976). [https://doi.org/10.1109/tassp.1976.1162830]
• S. E. Lee, S. Y. Chun, S. B. Hwang, and H. U. Lee, “Implementation of the omnidirectional target bearing detector utilizing towed linear array”, Journal of the Korea Institute of Military Science and Technology, vol. 5(no. 1), p59-64, (2002), (in Korean).
• A. Dresan, and Y. Tanik, “Passive radar location by time difference of arrival”, Proceedings of IEEE Military Communications Conference 2002, vol. 2, p1251-1257, (2002).
• M. S. Han, J. Y. Choi, D. S. Kang, K. Son, and P. H. Lee, “A study on optimal hydrophone arrangement for the direction finding of high speed moving target in underwater”, Journal of the Korea Institute of Military Science and Technology, vol. 20(no. 3), p369-375, (2017), (in Korean).
• C. Couvereur, and Y. Bresler, “Doppler-based motion estimation for wide-band source from single passive sensor measurements”, Proceedings of the 1997 IEEE International Conference on Acoustics, Speech, and Signal Processing, vol. 5, p3537-3540, (1997).
• Y. T. Chan, and F. L. Jardine, “Target localization and tracking from doppler-shift measurements”, IEEE Journal of Oceanic Engineering, vol. 15(no. 3), p251-257, (1990). [https://doi.org/10.1109/48.107154]
• V. Cevher, R. Chellappa, and J. H. Mcclellan, “Vehicle speed estimation using acoustic wave patterns”, IEEE Transactions on Signal Processing, vol. 57(no. 1), p30-47, (2009). [https://doi.org/10.1109/tsp.2008.2005750]
• S. Barnwal, R. Barnwal, R. Hegde, R. Sigh, and B. Raj, “Doppler based speed estimation of vehicles using passive sensor”, 2013 IEEE International Conference on Multimedia and Expo Workshops (ICMEW), p1-4, (2013). [https://doi.org/10.1109/icmew.2013.6618278]
• J. Li, and J. Zhang, “Research on the algorithm of multi-autonomous underwater vehicles navigation and localization based on the extended kalman filter”, 2016 IEEE International Conference on Mechatronics and Automation, p2455-2460, (2016). [https://doi.org/10.1109/icma.2016.7558951]