정전 시 공공기관 마이크로그리드의 분산전원 최적 운영 기법 연구

2.1 대상 공공기관의 마이크로그리드 구성

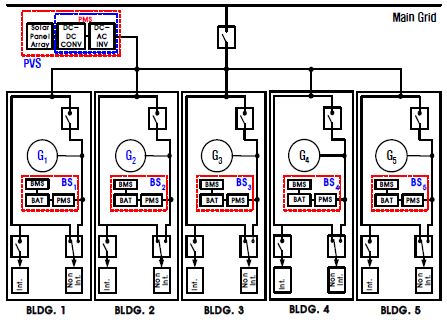
Figure 1은 대상 공공기관의 마이크로그리드 구성도를 나타낸 것으로, 그림에서 BLDG는 대상 공공기관에 속한 건물들 중 중요부하(Non-interruptible Load)들이 존재하는 5개 건물을 나타내고, G는 디젤발전기, BS는 배터리팩, BMS (Battery Management System) 및 PMS (Power Management System)를 포함한 배터리시스템, PVS (Photo-Voltaic System)는 태양광 패널 어레이와 PMS로 이루어진 태양광발전시스템, Non-Int.는 중요부하, 그리고 Int.는 일반부하로서 정전 시 전력이 공급되지 않아도 되는 부하를 나타낸다.

Figure 1:

The microgrid of the public institution

마이크로그리드 내에 기존 설치된 발전원은 5개 건물에 300 kW 디젤발전기 1대씩 모두 5대를 비롯해, 각 건물에 설치된 배터리시스템을 모두 합한 300kWh 배터리시스템 1세트, 80kW 태양광 발전시스템 1세트로 이루어져 있다. 이때 각 건물들 사이의 거리는 무시하여 선로손실은 없다고 가정한다. 실제로 건물들 사이의 이격거리는 100m에 가까운 것도 있으므로, 선로손실을 고려하여 인접한 디젤발전원부터 가동시키는 것이 올바른 방법이지만, 선로길이에 따른 영향은 무시할 수 있는 수준이므로 본 논문에서는 고려하지 않았으며, 수명을 늘이기 위해 각 디젤발전기의 가동시간 역시 균일하도록 유지해야 하나, 문제의 간략화를 위해 고려하지 않았다.

2.2 대상 공공기관의 일일 중요부하 변화

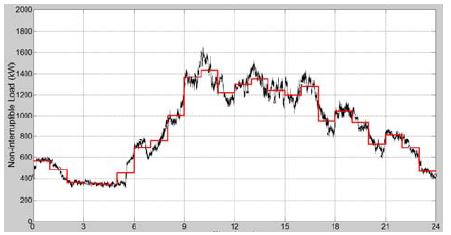
대상 공공기관의 중요부하는 주로 공조기, 조명, 서버, 전열기, 정밀계측기, 견인용 구동기 등으로 이루어져 있다. Figure 2는 공공기관의 5개 건물에 대해 연간 가장 부하량이 크고 변화도 심한 특정한 여름날의 전체 중요부하의 순시변화량을 측정한 것(검은 실선)과 이를 각 시간대별로 구분하여 평균값을 나타낸 것이다(붉은 실선).

Figure 2:

The non-interruptible load profile of the microgrid of the public institution for one day

그림에서 알 수 있듯이, 하루 중 중요부하의 전력사용량이 가장 많은 시간은 9시부터 저녁 6시 사이로 피크치는 1.6MW에 달하는데, 이는 주로 공조기와 견인용 구동기의 사용량이 크기 때문이며, 밤 11시부터 새벽 6시까지는 약 400kW 정도의 부하가 걸리고 있다.

2.3 디젤발전기 연료소모율

디젤발전기는 설치가 용이하고, 기동시간이 짧아 기동정지가 빈번히 일어날 수 있는 마이크로그리드의 중요부하 담당 전원으로 많이 사용되고 있다. 마이크로그리드에서 많이 사용되고 있는 수 백 kW급의 60Hz 디젤발전기들의 연료소모량을 분석해 보면, 출력의 50%와 100% 사이에서는 발전 효율과 밀접한 관련이 있는 출력 당 연료소모량이 거의 비슷하나, 50% 이하에서는 급격히 떨어짐을 알 수 있다.

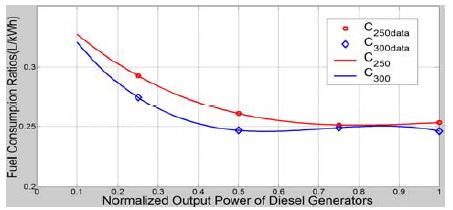
특히 250kW 및 300kW 디젤발전기에 대해 발전기 제작사가 제공하는 출력의 25%, 50%, 75%, 100%에서의 연료소모량의 값들(C_250data 및 C_300data)을 사용하여 그림의 실선과 같은 3차식을 만들어 그래프(C₂₅₀ 및 C₃₀₀)로 그린 것이 Figure 3에 주어져 있다. 그림에서 보듯이 발전기의 출력이 크면 출력 당 연료소모량도 다소 감소함을 알 수 있다. 특히 본 연구에서 대상으로 하고 있는 300kW급 디젤발전기를 보면, 출력의 50%와 100% 사이에서는 출력 당 연료소모량이 거의 비슷한 반면, 그 이하로 출력이 낮아질수록 연료소모량이 증가하여 20% 부근에서는 0.287L/kWh로서 50%일 때의 0.2467L/kWh보다 약 16.3% 정도 증가함을 Table 1로부터 알 수 있다.

Figure 3:

Fuel consumption ratios of 250kW and 300kW diesel generators

Table 1:

Fuel consumption ratios of 250kW and 300kW diesel generators

2.4 태양광발전시스템

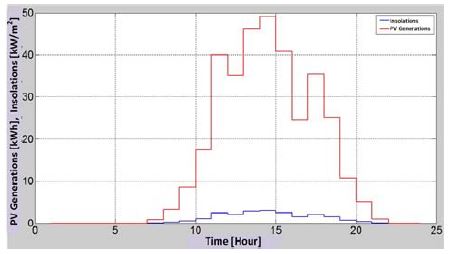
Figure 4는 중요부하를 측정한 당일에 대해, 기상청의 자료를 이용해 공공기관이 위치해 있는 창원지역의 시간 당 평균 일사량(파란 실선)을 기반으로 그때의 80kW 태양광 발전시스템의 발전량(붉은 실선)을 나타낸 것이다. 이때 대기의 청명도는 창원지역의 여름날 평균치인 0.6을 적용했다. 그림에서 보듯이 태양광발전시스템은 오전 9시경부터 오후 7시경까지 매 시간 약 8 ~ 48kWh의 전력량을 생산할 수 있다.

Figure 4:

Insolations in Changwon city where the public institution is located and photo-voltaic power generations for the same day

2.5 배터리시스템

각 건물에 설치된 배터리시스템의 용량은 20 ~ 100kWh로 다양하지만, 시뮬레이션 시에는 이들을 모두 합하여 하나의 300kWh 배터리시스템으로 다루었다. 이는 앞서 설명한 것과 마찬가지로 본 논문의 취지를 해치지 않으면서 문제를 간략화하기 위한 것이다. 배터리의 초기 SOC는 100%, 최소 SOC는 30%로 설정하였으며, 충방전효율은 100%로 가정하였다.

2.6 수리모델

디젤발전기의 총 효율이 최대(연료소모량이 최소)가 되도록 혼합정수계획법을 이용하여 단위시간별 대상시스템의 발전 용량을 결정하는 수리모델을 아래에서 제시하였다. 수리모델에서 고려한 가정은 다음과 같다.

•　 정전 시부터 전원복구 시까지 마이크로그리드의 독립운전이 가능한 한 오래 지속될 수 있도록 하는 것이 목적이므로, 배터리시스템의 충방전 횟수로 인한 수명 감소는 고려하지 않는다.
•　 각 발전원들은 기존에 설치되어 있기 때문에 초기투자비와 유지보수비는 고려하지 않는다.
•　 수리모델의 시간구간은 1시간으로 설정하였다. 각 시간대에 따라서는 중요부하의 전력순시치가 평균치에서 10% 이상 벗어나는 경우도 있기 때문에, 좀 더 정확한 운용계획을 세우기 위해서는 5분 또는 10분 등의 단위로 세분화할 수 있지만, 이는 단지 해를 구하는 시간이 늘어날 뿐 다른 영향은 없기 때문에, 문제를 간단히 하기 위해 1시간 단위로 구간을 정해도 본 논문의 취지는 훼손되지 않는다.
•　 독립모드로 운전되는 마이크로그리드의 시간대별 발전량은 부하전력을 만족시켜야 한다.
•　 독립모드로 운전되는 마이크로그리드는 동일 성능의 디젤발전기 5대, 배터리시스템 1세트, 태양광발전시스템 1세트 및 중요부하로 이루어져 있다.
•　 시간대마다 각 디젤발전기의 출력은 정격출력의 10% 단위로 달라질 수 있다.
•　 디젤발전기와 태양광발전시스템은 부하를 담당하거나 배터리를 충전시킬 수 있다.
•　 배터리시스템은 최초 시간대에 100%로 충전되어 있으며, 충방전 효율은 100%라고 가정한다.
•　 태양광발전시스템의 단위시간별 발전가능량은 주어져 있다.
•　 수명을 위해 배터리의 충전상태(State of Charge, 이하 SOC)는 30% 이하가 되지 않아야 한다.

본 연구에서 수립한 마이크로그리드의 최적 운용을 위한 수리모델과 입력데이터 및 의사결정변수는 다음과 같다.

A) 목적함수

B) 제약조건

C) 수리모델에서의 각 입력데이터와 의사결정 변수

식 (1)은 각 디젤발전기의 연료소모율의 합을 최소화하는 것으로서, 이때 목적함수값은 하루 동안 최적 운영 방안으로 가동된 디젤발전기들의 총 연료소모량을 나타낸다. 식 (2)는 각 시간대에서 디젤발전량과 배터리 보유 전력량, 태양광 발전량의 합은 부하전력의 크기보다 커야 함을 나타내고, 식 (3)은 디젤발전기가 여러 효율 중 하나의 형태로 발전하는 것을 의미한다. 식 (4)는 태양광 발전으로 생산된 전력은 부하를 담당하거나 배터리에 충전될 수 있음을 나타내고, 식 (5)는 배터리의 충방전에 관계되는 것으로, 각 발전시스템의 총 발전전력 중 부하를 담당하고 남은 전력은 다음 시간대를 위하여 배터리에 충전됨을 의미하며, 식 (6)은 수명을 고려하여, 배터리는 최대충전과 최소충전 상태 사이에서 동작해야 함을 나타낸다. 즉, 시간대별 배터리 용량은 최소 일정량(30%) 이상이 되어야 한다. 식 (7)은 배터리가 보유 전력량 한도 내에서 부하를 담당할 수 있다는 것이며, 식 (8)은 각 변수가 가질 수 있는 값의 범위를 나타내고 있다.

2.7 최적화 알고리즘을 이용한 시뮬레이션

이상과 같이 수립된 수리모델의 타당성을 평가하기 위해, 간단한 예를 통하여 제시된 수리모델을 검증하였다. 시뮬레이션에는 용량 300kW의 디젤발전기 5대와 300kWh 배터리시스템 1세트, 80kW 태양광 발전시스템 1세트로 이루어진 마이크로그리드를 대상으로 하였으며, 이때 디젤발전기는 4가지의 출력으로만 운전하며, 그때의 연료소모량 C_ij는 Table 2와 같다고 가정하였다.

Table 2:

Fuel consumption ratios according to output power of the diesel generator

또한 최적해를 구하기 위한 수행시간을 고려하여 시간대는 임의로 5구간만을 설정하였으며, 각 시간대별 중요부하의 크기와 태양광 발전시스템의 발전전력 또한 임의의 값을 설정하였다.

주어진 입력 자료를 바탕으로 운영체제 Window 7에서 Intel Core(TM) i3(3.6 GHz) CPU를 이용하여 Lindo(ver. 6.1) 프로그램을 최적화 수리모델에 적용한 결과, Table 3과 같은 최적해를 구하였다. 표에서 $$ P_L^t,P_{G1j},P_{G2j},P_{G3j},P_{G4j},P_{G5j},P_{PV}^t$$는 각각 부하전력량, 디젤발전기 1~5의 발전전력량, 태양광 발전기의 발전전력량을 나타내고, $$ P_B^t$$와 $$ P_B^{t+1}$$은 각각 현재 시간대 및 다음 시간대의 배터리 전력량을 나타내며, 이들의 단위는 모두 kWh이다. 표의 결과를 보면 태양광시스템은 항상 최대로 발전시켜 운용하고, 대부분의 중요부하 전력은 디젤발전기와 배터리시스템이 담당하는 것으로 나타났는데, 이는 직관적으로도 당연한 결과라 할 수 있으므로, 최적화 수리모델의 타당성은 입증되었다 할 수 있다. 또한 중요부하를 담당하고 남은 전력은 다시 배터리를 충전하는데 사용됨을 알 수 있다. 이때 최적해의 목적함수값, 즉 5시간 동안 가동된 발전기들의 총 연료소모량은 1,509L/kWh였으며, 최적해를 구하는데 소요된 시간은 2시간 25분이었다.

Table 3:

Simulation results of the optimization mathematical model

그러나 제시된 수리모형을 이용하여 실제 문제 크기인 하루 동안(즉 24개의 시간대)의 발전계획을 수립하기 위하여 최적화 알고리즘을 이용하여 시뮬레이션을 수행하였지만 최적해를 구하지 못하였다.

3.1 휴리스틱 알고리즘

본 연구에서는 빠른 시간 안에 각 발전시스템의 운용계획을 수립하면서도 최적에 가까운 해를 구하기 위해 수정된 수리모델을 이용한 휴리스틱 알고리즘을 제안하였다. 제안된 알고리즘의 수행절차는 다음과 같다.

단계 1)
각 시간대별로 배터리를 제외한 공급전력량(디젤발전기 및 태양광 발전시스템의 전력량의 합)과 중요부하의 크기를 파악한다. 이때 모든 시간대에서 공급전력량이 중요부하량 보다 클 때는 각 시간대별 필요전력량은 중요부하량과 동일하다. 만약 어떤 시간대에서 공급전력보다 중요부하가 크면 이를 병목(bottle neck)시간대라 하며, 배터리 전력량까지 사용해야만 중요부하에 전력을 공급할 수 있는 시간대이다. 이 경우 병목시간대에서 배터리가 공급해야 할 전력량(중요부하 전력량 - 디젤발전기 발전량 - 태양광 발전량)을 구하여 병목 앞 시간대에서 부족한 전력량만큼 배터리가 담당하게끔 설정한다. 만약 병목시간대가 연속적으로 발생하면, 모두 합한 부족전력량을 이전 시간대들로 최적으로 분산 배치시켜 배터리가 담당해야 될 전력량을 미리 결정한다.
단계 2)
단계 1에서 구한 각 시간대별 요구전력량을 만족시키기 위하여 태양광 발전전력을 우선 사용한 후, 부족한 전력은 연료소모량을 최소화할 수 있도록 디젤발전기를 가동시키며, 이때 전력요구량보다 남거나 부족한 부분은 배터리를 충전 또는 방전시킨다. 각 시간대마다의 효율적인 발전 계획은 다음과 같은 수정된 수리모델을 이용하여 최적해를 구한다.

A) 목적함수

B) 제약조건

수정된 수리모델의 목적함수는 앞서 제시된 최적화 수리모델의 목적함수에서 시간대 t가 빠진 것을 제외하고는 동일하다. 또한 제약조건은 디젤발전기의 총 발전량이 해당 시간대의 중요부하 전력요구량을 만족시켜야 한다는 식 (10)과 디젤발전기는 여러 효율 중 하나의 효율로 발전함을 나타내는 식 (11)이다. 이때 어떤 시간대에서 발전된 전력량 중 남은 것은 배터리를 충전시키며, 다음 시간대에서는 앞 시간대에서 충전된 배터리전력량을 고려하여 디젤발전기의 최적 운영 계획을 수립하게 된다. 따라서 제시된 수리모델은 각 단일 시간대에 대한 발전방안을 수립하는 것이기 때문에, 최적해를 빠른 시간 내에 구할 수 있다.

이상의 단계를 거쳐 공공기관의 마이크로그리드 최적운영 문제를 해결하기 위해 휴리스틱 알고리즘을 적용하였다.

3.2 Case 1

대상 마이크로그리드 시스템은 300kW 디젤발전기 5대, 300kWh 배터리시스템 1세트, 80kW 태양광발전시스템 1세트로 이루어져 있으며, 시간대별 중요부하 전력요구량과 태양광 발전량이 각각 Figure 2와 Figure 4로 주어진 경우, 정전 시 24시간 동안의 발전계획을 수립하기 위한 시뮬레이션을 수행하였다.

단계 1)
병목시간대는 존재하지 않는다. 추가적인 배터리 필요량은 고려하지 않아도 된다. 배터리의 총 용량 중에서 최소 보유 용량 75kWh를 제외한 175kWh가 사용가능한 최대 배터리 용량이 된다.
단계 2)
디젤발전기의 발전량은 전력요구량에서 태양광발전량과 앞 시간대에 남은 배터리 전력량을 빼서 구한다.

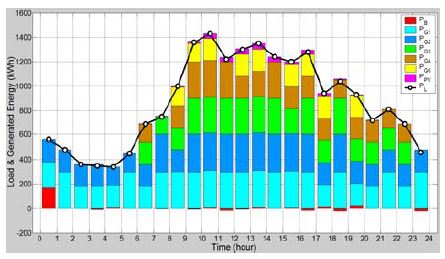
수정된 수리모델을 이용하여 다음 Table 4와 같은 시간대별 전력발전 계획을 얻었으며, 단위는 모두 kWh이다. 또한 Table 4를 그래프로 나타낸 것이 Figure 5로서, 배터리전력량은 붉은색으로 표시되어 있으며, 0kWh를 기준으로 양으로 표시된 것은 방전, 음으로 표시된 것은 충전되었음을 나타낸다.

Table 4:

Simulation results of performing the optimized solution using heuristic algorithms for Case 1

Figure 5:

The simulation results of the optimal management scheme using heuristic algorithms for Case 1

시뮬레이션 결과를 보면, 태양광 발전전력을 먼저 사용한 후, 디젤발전기는 연료소모량이 가장 낮은 출력(180kW)에서 가동시켜도 될 경우는 그 출력에서 가동시키고, 그 이상의 전력공급이 필요한 경우에는 그 다음으로 낮은 연료 소모량을 갖는 출력에서 가동시키는 전략을 취하고 있음을 알 수 있다. 즉 부하의 크기로부터 필요한 디젤발전기 대수에 대하여 연료효율이 가장 좋은 것부터 고려하여 필요한 발전용량 조합을 구하고, 사용하고 남거나 모자라는 전력은 배터리를 충전 또는 방전시킨다.

이때 제안된 휴리스틱 알고리즘으로 구한 해의 목적함수값(5대 디젤발전기의 총 연료소모량)은 5,034.4L이었다. 반면에 Lindo 프로그램을 이용하여 최적화 수리모델인 식 (1) ~ 식 (8)에 적용한 시뮬레이션 결과, 천만회의 반복시행으로 7시간 동안 탐색하였으나 최적해는 구하지 못하였고, 그때까지 얻어진 목적함수의 하한값은 5,007.3L이었으며, 그때까지 구한 해 중 가장 좋은 값은 5,011.0L로 나타났다.

제안된 휴리스틱 알고리즘으로 구한 해의 목적함수 값은 최적화 알고리즘으로 천만 회 반복하여 구한 하한값 대비 최대 100.5%(5,034.4/5,011.0 × 100)로서, 매우 우수한 성능을 가진 해법임을 알 수 있다. 또한 휴리스틱 알고리즘을 이용한 최적해 탐색시간은 수 초로서 거의 시간이 걸리지 않았다.

3.3 Case 2

앞서 다루었던 문제 조건에서는 병목시간대가 존재하지 않았기 때문에, 제안된 휴리스틱 문제해결 방안의 타당성을 검증하기 위해 병목시간대가 존재하는 가상의 마이크로그리드를 설정하여 최적운영 방안을 도출하였다. 이때 시간대별 중요부하의 크기는 Case 1과 동일하며, 그리드 내 각 발전원은 250kW 디젤발전기 5대, 350kWh 배터리시스템 1세트, 80kW 태양광 발전시스템 1세트로 설정하였으며, 250kW 디젤발전기의 출력별 연료소모량은 Table 1과 같다.

단계 1)
배터리의 총 용량 중에서 최소 보유 용량 105kWh를 제외한 245kWh가 사용가능한 최대 배터리용량이 된다. 중요부하량이 배터리를 제외한 전력량(이 경우는 5대 디젤발전기의 발전량 250 × 5 = 1,250kWh과 해당 시간대의 태양광발전량을 합한 값)보다 클 때인 병목시간대는 9-10, 10-11, 12-13, 13-14 시간대로 총 4구간(표에서 회색으로 표시된 시간대)에서 발생한다. 따라서 9-10 시간대에서는 93kWh(1360 – 17 – 250 × 5 = 93), 10-11 시간대에서는 140kWh(1430 – 40 – 250 × 5 = 140)가 부족하므로, 8-9 시간대에서 앞의 두 시간대에서 부족한 233kWh(93 + 140kWh)를 추가로 발전시켜 배터리에 저장한다. 마찬가지로 11-12 시간대에서는 55kWh, 12-13 시간대에서는 51kWh의 추가전력을 발전시켜야 한다.
단계 2)
수정된 전력수요량을 기준으로 태양광 발전량과 배터리용량을 고려하여 단일 시간대에 대하여 순차적으로 휴리스틱 수리모델을 적용함으로써 최적 디젤발전조합을 결정한다.

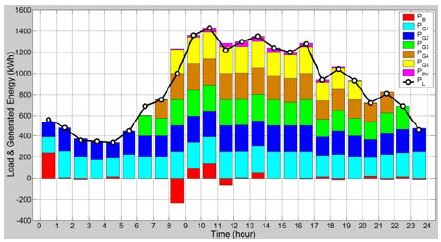
수정된 수리모델에 휴리스틱 알고리즘을 적용시켜 시뮬레이션한 결과가 Table 5에 주어져 있으며, 이를 그래프로 나타낸 것이 Figure 6이다.

Table 5:

Simulation results of performing the optimized solution using heuristic algorithms for Case 2

Figure 6:

The simulation results of the optimal management scheme using heuristic algorithms for Case 2

시뮬레이션 결과를 보면 병목시간대 바로 앞인 8-9시간대에서는 해당 시간대에서 필요한 부하전력량 1,000kWh와 뒤의 병목시간대에서 필요로 하는 추가 배터리용량 233kWh에 대한 발전계획이 필요하다. 태양광 발전량 9kWh와 4대의 디젤발전기에서 각 250kWh씩 1,000kWh를 생산하고 나머지 1대의 디젤발전기로 225kWh를 생산함으로써 총 1,234kWh를 생산하여 해당 시간대의 부하량 1,000kWh를 담당하고 남은 234kWh를 배터리에 충전하여 총 배터리의 전력량은 238kWh가 되도록 발전 계획을 수립하여 다음 병목시간대의 부족전력량 233kWh를 준비하는 것을 알 수 있다.

또한 제안된 휴리스틱 알고리즘으로 구한 해의 목적함수값은 5,118.2 L이었으며, 탐색시간은 10초 이내였다. 반면에 Lindo 프로그램을 이용하여 최적화 수리모델에 적용한 시뮬레이션 결과, 천만회의 반복시행으로 7시간 동안 탐색하였으나 역시 최적해는 구하지 못하였고, 그때까지 얻어진 목적함수의 하한값은 5,103.2L이었으며, 그때까지 구한 해 중 가장 좋은 값은 5,131.1L로 나타났다.

제안된 휴리스틱 알고리즘으로 구한 목적함수값이 최적화 수리모델에서 구한 가장 좋은 값보다 오히려 더 나은 결과를 나타내었는데, 이는 최적화 알고리즘으로 같은 값을 얻으려면 훨씬 더 많은 계산시간을 거쳐야 한다는 것을 의미한다. 휴리스틱 알고리즘으로 구한 해의 목적함수값은 최적화 알고리즘으로 구한 하한값 대비 100.3 % (5,118.2/5,103.2 × 100)로서, 매우 우수한 성능을 가진 기법임을 다시 한 번 입증되었다.

아래 Table 6은 Case 1과 2에 대하여 최적화 알고리즘과 휴리스틱 알고리즘의 결과를 비교, 요약한 것이다.

Table 6:

Comparison of the simulation results between the optimization algorithm and the heuristic algorithm