난류 예혼합 화염의 평균방향벡터와 평균곡률에 대한 수치적 연구

1. 서 론

난류 예혼합 연소는 실생활과 산업에 이용되는 많은 에너지 변환기기에서 나타나는 복합적인 물리 현상이다. 그 대표적인 예로 차량, 선박용 내연기관과 발전, 항공기용 가스터빈 엔진과 같은 연소기들을 들 수 있다. 연소기의 높은 에너지변환 효율과 엄격한 배출가스규제를 동시에 충족시키기 위해 연소기의 설계조건은 나날이 까다로워지고 있다.

연소기의 설계 및 개발 단계에서 시간과 비용의 절감을 위하여 수치해석기법의 활용이 증가되는 추세이고, 고 정확도의 난류연소해석을 위해 필요한 난류연소모델의 개발에 관한 연구도 지속되고 있다[1]. 난류 예혼합 연소 모델로서 층류 화염편 모델에 기초한 G방정식 모델[2]은 대 와동모사에 적용되어 보염기 주위의 난류 예혼합 연소 유동을 모사하는 등[3] 널리 이용되고 있지만, 모델의 근간이 되는 층류 화염편 모델의 개념에 대한 보완의 필요성도 보고되고 있다[4].

최근 심각한 환경문제로 대두되고 있는 미세먼지와 관련이 높은 soot 생성에 관하여 국내외적으로 실험적, 수치해석적 연구가 활발히 진행되고 있다[5][6]. Soot, NOx, SOx 등의 배기배출에 대한 수치해석적 예측 정확성은 난류연소 해석의 정확성과 직결되므로 고 정확도의 난류연소모델 개발의 중요성은 더욱 커졌다.

본 연구에서는 난류연소모델의 개발과 관련이 높은 난류 예혼합 화염의 중요 매개변수들에 대한 지배방정식이 유도되었고, 직접수치해법을 통해 구현한 화염들을 대상으로 유도된 지배방정식의 검증 및 각 성분항의 중요도를 살펴보았다. 난류 예혼합 연소에서 화학 반응이 일어나는 영역은 일반적으로 반응진행변수 c에 의해 설명되며, 이는 온도 또는 반응물 중 부족한 화학종의 농도로부터 정의된다. 반응진행변수는 미연 가스에서는 0이며, 완전 연소된 가스에서는 1의 값을 가진다. 높은 Damkohler 수를 가지는 연소 영역에서 형성된 얇은 화염 내부에서 반응진행변수는 0과 1사이에서 변하게 된다. 주어진 도메인 내에서 반응진행변수의 확률밀도함수와 화염 관련 모든 스칼라 및 벡터의 평균을 얻으려면 반응진행변수의 평균값 $$ \stackrel{-}{c}$$에 대한 정보가 중요하다. 반응진행변수의 수송식은 연속체 형태[7]와 표면 전파 형태[8]의 두 가지로 나타낼 수 있다. 전자는 난류 플럭스의 평균 반응항과 역구배 확산을 포함하고 후자는 대류 속도와 화염의 변위 속도가 화염 표면을 따라 넓은 범위에서 변한다. 두 가지 형태의 수송식 모두에서 평균 반응 속도, 난류 플럭스 및 화염브러쉬를 통한 화염 표면의 이동을 결정하기 위해서는 화염의 내부 구조 및 통계적 특성을 이해하는 것이 중요하다. 따라서 본 연구에서는 난류 예혼합 화염의 통계적 거동을 일관되게 설명하기 위해 표면 전파 형태의 반응진행변수 수송식으로부터 평균반응진행변수, 화염면적밀도(flame surface density, FSD), 평균방향벡터 및 평균곡률에 대해 조건평균을 이용한 새로운 수송식을 유도하였다.

2. 평균방향벡터와 평균곡률의 수송식 유도

반응진행변수 c의 수송식은 식 (1)과 같다.

여기서 ρ는 밀도, v는 대류속도, D_m은 분자확산계수, $$ {\dot{w}}_c$$는 반응진행변수의 생성률이다. 식 (1)의 표면 전파 형태는 식 (2)와 같다.

여기서 대류속도의 법선성분 v_n은 대류속도와 방향벡터와의 내적인 υ·n으로 정의되며, 화염면의 방향벡터(n)은 $$ n=-\frac{\nabla c}{\left|\nabla c\right|}$$, 화염면적함수$$ \left({\mathrm{\Sigma }}_f^{\text{'}}\right)$$는 $$ {\mathrm{\Sigma }}_f^{\text{'}}=\left|\nabla c\right|$$, 연소속도(S_d)는 $$ S_d=\frac{1}{{\mathrm{\Sigma }}_f^{\text{'}}}\left(\frac{1}{\rho }\nabla \cdot \left(\rho D_m\nabla c\right)+{\dot{w}}_c\right)$$으로 정의된다. 따라서 $$ \nabla c=-n{\mathrm{\Sigma }}_f^{\text{'}}$$ 와 $$ {\mathrm{\Sigma }}_f^{\text{'}}=-\frac{\partial c}{\partial n}$$이 성립한다. 난류 예혼합 화염의 내부구조 및 전파특성을 해석하기 위한 조건평균과 편차는 화염면적밀도를 이용하여 주어진 스칼라나 벡터에 대해 식 (3), 식 (4)와 같이 정의한다.

방향벡터 n에 대한 수송식을 유도하기 위해 식 (2)에 구배 연산자(gradient operator)를 적용하면 식 (5)를 얻게 된다.

여기서 (v_n+S_d)는 미연 가스 방향으로 움직이는 화염의 법선방향 속도를 나타내며, ∇_T 는 접선구배 연산자로서 스칼라 ϕ에 대해 $$ {\nabla }_T\varphi =\nabla \varphi =n\frac{\partial \varphi }{\partial n}$$으로 정의한다. 화염면적함수에 대한 수송식을 유도하기 위해 방향벡터(n)와 식 (5)의 내적을 취하면 식 (6)이 유도된다.

식 (6)을 평균하면 참고문헌[9][10]에 나오는 종래의 수식과 동등한 형태의 식 (7)이 유도됨을 알 수 있다.

화염면의 곡률 ∇·n에 대한 수송식을 유도하기 위해 식 (2)의 양변에 ($$ \frac{{\partial }^2}{\partial n^2}-{\nabla }^2$$) 연산을 수행하고, 반응진행변수의 2계 미분에 대한 관계식 $$ \frac{{\partial }^{2}c}{\partial n^2}-{\nabla }^{2}c={\mathrm{\Sigma }}_f^{\text{'}}\nabla \cdot n$$[11]을 대입하면 식 (8)이 유도된다.

평균진행변수와 평균화염면적밀도에 대한 수송식은 식(2)와 식 (6)을 평균하여 각각 식 (9)와 식 (10)으로 유도된다.

난류 예혼합 화염이 통계적 정상상태에 도달하면 시간에 대한 미분항이 소거되므로 식 (11)과 식 (12)가 성립한다.

식 (5)를 평균하면 평균방향벡터 <n>_f에 대한 수송식이 식 (13)과 같이 유도된다.

마지막으로 식 (8)을 평균하고 식 (9)와 식 (10)을 대입하면 평균곡률에 대한 수송식인 식 (14)가 유도된다.

3. 직접수치해석 계산조건

3.1 비압축성 자유전파화염

3차원 직접수치해석을 이용하여 비압축성 난류 유동장에서 형성된 자유전파화염을 구현하였으며, Figure 1 (a)는 화염의 형상을 보여준다. 스펙트럴 기법에 기반하여 비압축성 등방성 난류 유동장을 생성하였고, 유한차분법(finite dif-ference method)을 이용하여 반응물의 질량 분율에 대한 스칼라 수송을 계산한다. 공간 차분을 위해 6계 compact scheme을 적용하였고[12], 시간 적분을 위해 4계 Runge-Kutta 기법을 적용하였다[13]. 화학반응은 식 (15)와 같은 Arrhenius 형태의 비가역 단일단계반응을 가정하였다.

Figure 1:

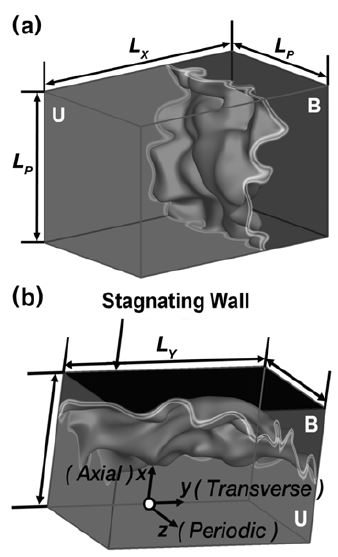
Configurations for (a) incompressible freely propagating flames and (b) a compressible stagnating flame

$\[ {\dot{w}}_c=A\rho \left(1-c\right)\text{exp}\left(-\frac{\beta }{\alpha }\right)\text{exp}\left(-\frac{\beta \left(1-c\right)}{1-\alpha \left(1-c\right)}\right) \]$

(15)

여기서 A는 화학반응상수이며, 열방출 매개변수(α)는 $$ \alpha =\frac{T_b-T_u}{T_b}$$, Zel’dovich 수(β)는 $$ \beta =\frac{E_a\left(T_b-T_u\right)}{R{T}_b^2}$$으로 정의되며, E_a는 활성화에너지, T_b는 기연가스 온도, T_u는 미연가스 온도, R은 기체상수이다. Table 1에 계산에 사용된 값을 나타내었으며, 화염이 생성되는 연소영역은 Table 2에 나타난 무차원 수를 통해 나타내었다. 계산 영역의 크기는 F1에 대하여 Lx ✕ Lp ✕ Lp = 3π ✕ 2π ✕ 2π, F2에 대하여 Lx ✕ Lp ✕ Lp = 5π ✕ 2π ✕ 2π으로 설정하였으며, 균일격자를 2π당 162개 사용하여 층류화염두께($$ {\delta }_L^0$$) 내부에 최소 7개의 격자점이 포함된다. 그 외 계산조건에 대한 상세사항은 D. Lee와 K. Y. Huh [14]을 참조하였다.

Table 1:

Physical parameters of F1, F2 and F3

Table 2:

Specifications of three test flames

4. 결과 및 고찰

Figure 2는 F1, F2 및 F3에 대한 c 분포의 순간 이미지를 보여준다. F1과 F2는 동일한 층류 화염 특성을 공유하며 각각 난류 예혼합 연소영역 중 wrinkled flamelet 영역과 thin reaction zone 영역에 해당한다. F2는 F1보다 더 강한 난류 하에서 화염편의 상당한 팽창을 보여주며, 화염브러쉬 양단에서 곡률의 급격한 변화를 관찰할 수 있다. 또한 화염면이 유지되지 못하고 분리되면서 섬 형태로 떨어져 나간 부분이 관찰되는데 이것은 난류의 영향으로 화염 양단의 곡률이 증가함에 따른 것으로 층류화염편 가정이 모든 연소영역에서 성립하지 않는다는 것을 보여준다. Figure 2 (c)는 압축성 유동장에서 구현된 화염이지만 Figure 2 (a)와 유사한 화염 형상을 보여주며 corrugated flame 영역에 해당한다.

Figure 2:

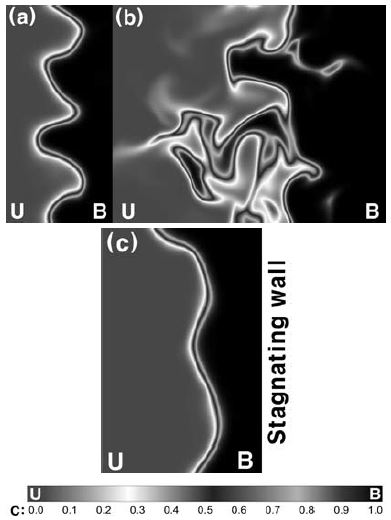
Instantaneous images of c distribution in (a) F1 (b) F2 and (c) F3. “U” and “B” represent unburned and burned gas

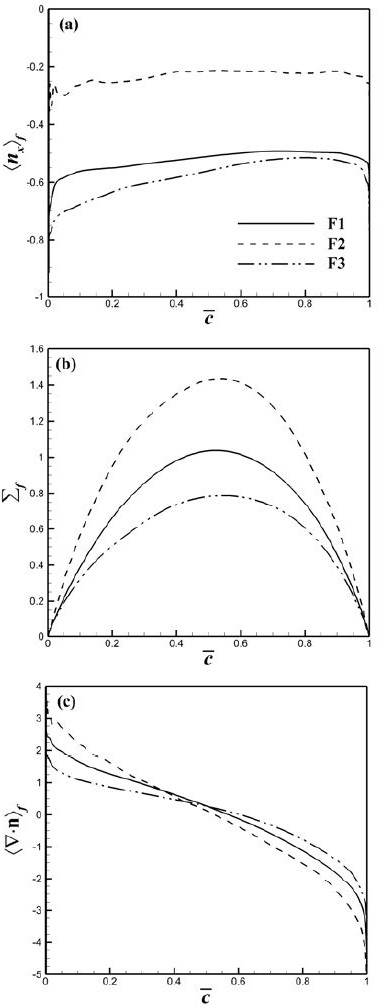
Figure 3은 세 가지 화염브러쉬 내부에서 <n_x>_f, ∑_f 및 <∇·n>_f의 분포가 크기는 다르지만 유사한 형태로 변화하는 것을 보여준다. F2는 상대적으로 강한 난류 조건으로 인해 세 화염 중 가장 작은 |<n_x>_f|을 보여주는데 이것은 화염의 전파방향이 일정하지 않다는 것을 의미한다. 또한 ∑_f와 |<∇·n>_f|는 모두 F2에서 가장 큰 값을 가지는데 이것은 난류강도가 증가함에 따라 화염면적이 증가하고 곡률이 증가함을 의미한다. ∑_f의 최대값은 $$ \overline{c}$$= 0.5보다 약간 큰 곳에서 나타나는데, 난류 예혼합 화염의 내부 구조에서 반응-확산층이 대류-확산층보다 화염의 후단에 있기 때문에 반응-확산층 근처에서 최대 ∑_f가 형성된다. <∇·n>_f는 화염의 양단을 제외한 브러쉬 내부에서 거의 선형적으로 감소하는 형태를 보여주며, 화염의 양단으로 갈수록 절대값이 급격히 증가한다.

Figure 3:

Distributions of (a) <nx>f (b) Σf and (c) <∇·n>f in the c¯ space

$$ \frac{1}{{\mathrm{\Sigma }}_f^{\text{'}}}\frac{{\partial }^{2}c}{\partial n^2}$$는 평균방향벡터와 평균곡률의 수송식에 모두 나타나는 중요한 항으로서 층류화염 내부에서의 분포를 Figure 4 (a)에서 확인할 수 있으며, 길이 스케일의 역수로서 화염선단에서 후단으로 가면서 양의 값에서 음의 값으로 감소한다. $$ {〈\frac{1}{{\mathrm{\Sigma }}_f^{\text{'}}}\frac{{\partial }^{2}c}{\partial n^2}〉}_f$$은 화염 선단에서 양의 값을 가지며 그 이유는 Figure 4 (b)에 나타난 것처럼 양의 평균곡률을 가지는 화염선단에서 $$ \frac{1}{{\mathrm{\Sigma }}_f^{\text{'}}}\frac{{\partial }^{2}c}{\partial n^2}$$의 값이 양인 가스부피가 음인 가스부피보다 더 크기 때문이다. 반대 이유로 화염후단에서는 음의 값을 가진다.

Figure 4:

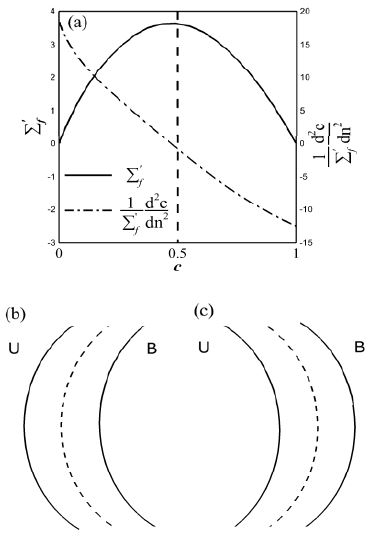
(a) Distributions of Σf' and 1Σf'∂2c∂n2 in a laminar flamelet, (b) flame configuration with positive curvature and (c) flame configuration with negative curvature. “U” and “B” represent unburned and burned gas

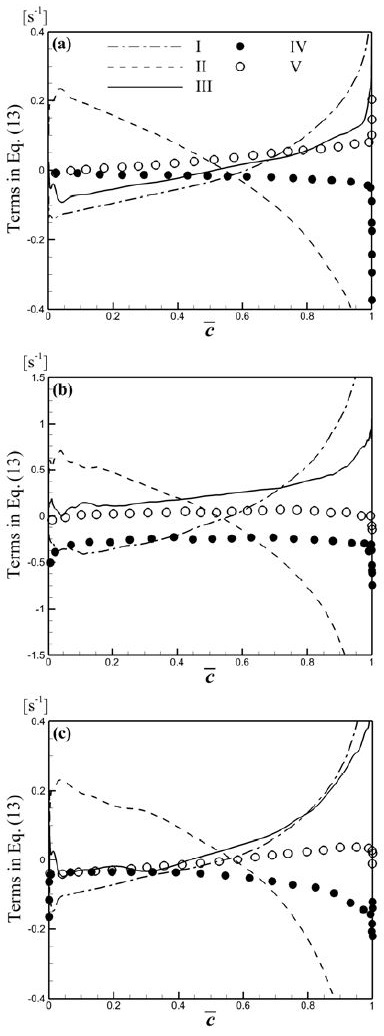
Figure 5는 통계적 정상상태에 있는 난류 예혼합 화염에 대하여 화염브러쉬 내에서 식 (13)의 모든 항의 x성분 분포를 보여준다. 식 (13) 우변에 있는 5개 항 중에서 I, II 항이 지배적인 항으로 나타나는데, I항은 (v_n+S_d)의 접선방향 구배의 조건평균으로서 화염의 선단에서 음의 값을 가지고 화염의 후단에서 양의 값을 가진다. II항은 I항과 반대로 화염의 선단에서 양의 값을 가지고 후단에서 음의 값을 가진다. 2개 항 모두 화염브러쉬 내부에서 양단으로 갈수록 급격한 변화를 보이며 선단보다는 후단에서의 절대값이 더 크다. 이러한 경향은 조건평균에 사용된 화염면적밀도의 c 공간에서의 구배가 화염후단에서 더 큰 것과 관련이 있는 것으로 이해되지만 일정 부분은 후처리 방법 때문에 화염 양단에서의 변화가 더 급격해 보일 수도 있다. 다시 말해 조건평균을 유동방향이 아닌 c 공간에서 도시함으로써 실제 물리적인 영역보다 c 공간에서의 변화가 더 압축되게 나타나는 것일 수도 있다. III항은 n_x, (v_n+S_d), $$ \frac{1}{{\mathrm{\Sigma }}_f^{\text{'}}}\frac{{\partial }^{2}c}{\partial n^2}$$의 3중 2개 항 모두 화염브러쉬 내부에서 양단으로 갈수록 급격한 변화를 보이며 선단보다는 후단에서의 절대값이 더 크다. 이러한 경향은 조건평균에 사용된 화염면적밀도의 c 공간에서의 구배가 화염후단에서 더 큰 것과 관련이 있는 것으로 이해되지만 일정 부분은 후처리 방법 때문에 화염 양단에서의 변화가 더 급격해 보일 수도 있다. 다시 말해 조건평균을 유동방향이 아닌 c 공간에서 도시함으로써 실제 물리적인 영역보다 c 공간에서의 변화가 더 압축되게 나타나는 것일 수도 있다. III항은 n_x, (v_n+S_d), $$ \frac{1}{{\mathrm{\Sigma }}_f^{\text{'}}}\frac{{\partial }^{2}c}{\partial n^2}$$의 3중 상관관계를 나타내는 것으로 화염 선단에서는 큰 의미가 없으나 화염 후단으로 가면서 크기가 급격히 증가하며, 압축성 정체화염인 F3의 경우 화염 후단에서 I항과 비슷한 크기를 가진다. 이러한 차이는 유동장의 특성 및 직접수치해석 기법과 관련이 있는데 비압축성 유동의 경우는 운동량과 에너지 보존이 분리되어 계산되므로 에너지 수송이 유동장에 영향을 주지 않지만 압축성 유동의 경우는 화염 후단에서의 급격한 부피 팽창과 더불어 운동량과 에너지 보존을 연립하여 풀이하는 수치해석기법의 차이로부터 유동과 화학반응의 상관관계가 더 크게 나타나는 것으로 판단된다. IV항은 비압축성 화염인 F1과 F2의 화염브러쉬 내부에서는 큰 변화를 보이지 않고, F2에서만 의미있는 크기를 가지는데 이는 난류강도의 증가에 따라 화염면의 방향과 화염전파속도의 법선방향의 구배 사이에 상관관계가 커진다는 것을 의미한다. F3의 경우 화염 선단에서는 무시할 정도의 값을 가지지만 후단으로 갈수록 감소하는 경향을 보이며, 이는 화염의 방향이 보다 불규칙적일수록 화염면의 법선방향으로 화염면의 전파속도의 구배가 커지는 것을 의미한다. V항은 화염면의 전파속도와 화염면적밀도의 접선방향 구배 사이의 상관관계를 의미하는 항으로서 세 가지 화염 모두에서 상대적으로 무시할만한 크기를 가진다. 즉, 화염의 전파속도는 접선방향으로 형성되는 화염면적밀도 구배와는 상관관계가 없는 것으로 해석할 수 있다.

Figure 5:

x-component terms of Eq. (13) in (a) F1, (b) F2 and (c) F3

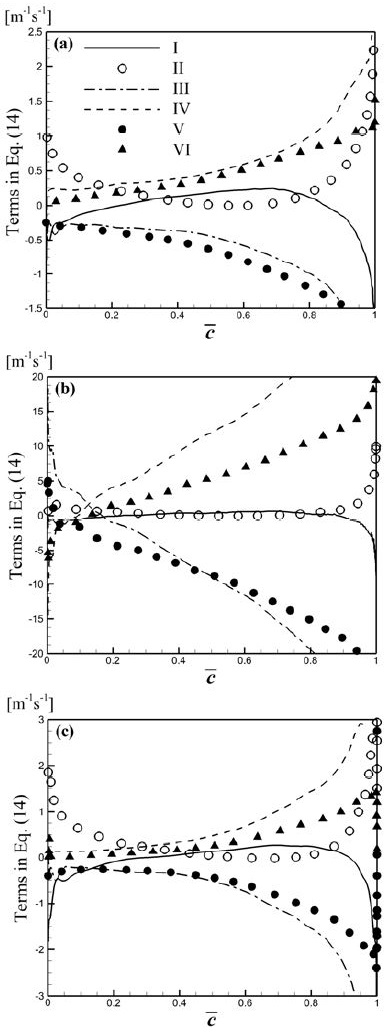
Figure 6는 통계적 정상상태에 있는 난류 예혼합 화염에 대하여 화염브러쉬 내에서 식 (14)의 모든 항의 분포를 보여주며, 평균곡률의 거동에서 III-VI 4개 항이 중요한 의미를 가지고 있다. I항은 화염브러쉬 양단을 제외하면 무시할만한 크기를 보여준다. II항도 마찬가지이나 그 경향이 I항과 반대로 나타난다. 논문에 나타내진 않았으나 후처리 결과 II항을 구성하는 성분 중 $$ {〈{\left(\nabla \cdot n\right)}^{"}{v}_n^{"}〉}_f$$은 양의 값으로 화염 양단을 제외하면 거의 일정한 값을 가지며, $$ {〈{\left(\nabla \cdot n\right)}^{"}{S}_d^{"}〉}_f$$은 음의 값으로 화염 후단으로 갈수록 중요한 의미를 가진다. 그러나 2개 성분의 합은 화염 선단에서 양의 값을 가지고 화염 후단에서 음의 값을 가진다. III항은 ∇·n, (v_n+S_d), $$ \frac{1}{{\mathrm{\Sigma }}_f^{\text{'}}}\frac{{\partial }^{2}c}{\partial n^2}$$의 3중 상관관계를 나타내는 것으로 대부분의 화염브러쉬 영역에서 음의 값을 가지며 화염후단으로 갈수록 감소한다. IV항은 화염 후단으로 갈수록 증가하고 III항과 반대되는 경향의 거동특성을 보여주며, 크기는 III항과 비슷하다. IV항의 구성성분 중 $$ {〈{\left(\nabla \cdot n\right)}^{"}{\left(\frac{\partial v_n}{\partial n}\right)}^{"}〉}_f$$는 무시가능하나 $$ {〈{\left(\nabla \cdot n\right)}^{"}{\left(\frac{\partial S_d}{\partial n}\right)}^{"}〉}_f$$은 음의 값을 가지며 화염 후단으로 갈수록 중요한 의미를 가진다. V항은 화염면 전파속도의 접선방향 구배와 화염면적밀도의 접선 방향 구배 사이의 상관관계를 나타내는 것으로 F1-F3 모든 경우에서 화염 후단으로 갈수록 감소하는 경향을 보인다. 후처리 결과 v_n과 S_d의 접선방향 구배는 서로 반대되는 경향을 보였으며, 비압축성 화염의 경우 화염 후단에서 S_d의 접선방향 구배가 지배적이고, 압축성 화염의 경우 화염 양단에서 S_d의 접선방향 구배가 지배적이다.

Figure 6:

Component terms of Eq. (14) in (a) F1, (b) F2 and (c) F3

5. 결 론

난류 예혼합 화염의 전파특성에 중요한 영향을 미치는 화염면의 평균방향벡터(<n>_f)와 평균곡률(<∇·n>_f)에 대한 조건평균 기반의 지배방정식이 유도되었다. 통계적 정상상태의 비압축성 자유전파화염과 압축성 정체화염을 대상으로 지배방정식의 평형을 확인하였으며, 화염브러쉬 내부에서 지배방정식을 구성하는 각 항의 거동특성을 파악하였다.

평균방향벡터의 거동은 지배방정식에서 ∇_T(v_n+S_d)와 n″(v_n+S_d)″를 포함하는 I, II, III항에 의해 지배적인 영향을 받으며, 난류 강도의 증가로 화염브러쉬의 두께가 두꺼워진 경우에는 화염 전파방향으로 형성되는 화염면 전파속도 구배인 $$ \frac{\partial \left(v_n+S_d\right)}{\partial n}$$를 고려해야 하며 이는 층류화염편 모델에서 화염 두께에 의한 전파특성을 보완해 주어야 함을 의미한다.

평균곡률의 거동은 지배방정식에서 III, IV, V, VI 4개 항에 의해 지배적인 영향을 받으며, 음의 평균 곡률을 가지는 화염브러쉬 후단에서 $$ \nabla \cdot n, v_n+S_d, \frac{\partial \left(v_n+S_d\right)}{\partial n},\mathrm{ }\frac{1}{{\mathrm{\Sigma }}_f^{\text{'}}}\frac{{\partial }^{2}c}{\partial n^2}, {\nabla }_T\left(v_n+S_d\right), \frac{1}{{\mathrm{\Sigma }}_f^{\text{'}}}{\nabla }_T{\mathrm{\Sigma }}_f^{\text{'}}$$ 항 사이의 강한 상관관계에 의해 화염브러쉬 후단으로 갈수록 발산하는 경향을 보인다.

본 연구결과 새롭게 유도된 지배방정식의 평형과 각 항 사이의 거동은 일정부분 파악되었지만 난류 상황에서 다양한 화염 매개변수들 간의 상관관계에 대한 보다 심도있는 연구가 필요하며, 이러한 기초 연구는 난류화염전파속도의 모델링에 큰 기여를 할 것으로 기대된다.

References

• D. Veynante, and L. Vervisch, “Turbulent combustion modeling”, Progress in Energy and Combustion Science, vol. 28(no. 3), p193-266, (2002).
• A. R. Kerstein, W. T. Ashurst, and F. A. Williams, “Field equation for interface propagation in an unsteady homogeneous flow field”, vol. 37(no. 7), p2728-2731, (1988). [https://doi.org/10.1103/physreva.37.2728]
• N. S. Park, and S. C. Ko, “Large eddy simulation of turbulent premixed combustion flow around bluff body based on the G-equation with dynamic sub-grid model”, Journal of the Korean Society of Marine Engineering, vol. 34(no. 8), p1084-1093, (2010), (in Korean). [https://doi.org/10.5916/jkosme.2010.34.8.1084]
• J. Kwon, Y. Park, and K. Y. Huh, “Flamelet characteristics at the leading edge and through the flame brush of statistically steady incompressible turbulent premixed flames”, Combustion and Flame, vol. 164, p85-98, (2016). [https://doi.org/10.1016/j.combustflame.2015.11.003]
• M. W. Bae, and S. W. Ahn, “A study on the effect of turbulent combustion upon soot formation in premixed constant-volume propane flames”, Journal of the Korean Society of Marine Engineering, vol. 27(no. 7), p889-898, (2003), (in Korean).
• I. M. Kennedy, “Models of soot formation and oxidation”, Progress in Energy and Combustion Science, vol. 23(no. 2), p95-132, (1997). [https://doi.org/10.1016/s0360-1285(97)00007-5]
• K. N. C. Bray, P. A. Libby, G. Masuya, and J. B. Moss, “Turbulence production in premixed turbulent flames”, Combustion Science and Technology, vol. 25(no. 3-4), p127-140, (1981). [https://doi.org/10.1080/00102208108547512]
• F. A. Williams, J. Buckmaster (Ed.), The Mathematics of Combustion, Philadelphia, Society for Industrial and Applied Mathematics, p97-131, (1985).
• S. B. Pope, “The evolution of surfaces in turbulence”, International Journal of Engineering Science, vol. 26(no. 5), p445-469, (1988). [https://doi.org/10.1016/0020-7225(88)90004-3]
• S. M. Candel, and T. J. Poinsot, “Flame stretch and the balance equation for the flame area”, Combustion Science and Technology, vol. 70(no. 1-3), p1-15, (1990). [https://doi.org/10.1080/00102209008951608]
• K. Y. Huh, J. Kwon, and D. Lee, “Relationships for maximum flame surface density and brush thickness through conditional analysis in turbulent premixed combustion”, Physics of Fluids, vol. 25(no. 7), p075108, (2013). [https://doi.org/10.1063/1.4816289]
• S. K. Lele, “Compact finite difference schemes with spectral-like resolution”, Journal of Computational Physics, vol. 103(no. 1), p16-42, (1992). [https://doi.org/10.1016/0021-9991(92)90324-r]
• C. A. Kennedy, M. H. Carpenter, and R. M. Lewis, “Low-storage, explicit Runge–Kutta schemes for the compressible Navier–Stokes equations”, Applied numerical mathematics, vol. 35(no. 3), p177-219, (2000). [https://doi.org/10.1016/s0168-9274(99)00141-5]
• D. Lee, and K. Y. Huh, “Statistically steady incompressible DNS to validate a new correlation for turbulent burning velocity in turbulent premixed combustion”, Flow, Turbulence and Combustion, vol. 84(no. 3), p339-356, (2010). [https://doi.org/10.1007/s10494-009-9221-3]
• D. Lee, and K. Y. Huh, “Validation of analytical expressions for turbulent burning velocity in stagnating and freely propagating turbulent premixed flames”, Combustion and Flame, vol. 159(no. 4), p1576-1591, (2012). [https://doi.org/10.1016/j.combustflame.2011.11.007]