Performance improvement for velocity controller of fish sorting belt conveyor system under bounded disturbance in transient phase

1. Introduction

In a fish sorting system (FSS), captured fishes are transported by a fish pump from a ship into a fish sorting line through a conveyor system. The captured fishes are sorted by the injury rate, which is estimated by using an image processing system. Thus, the conveyor system speed plays a key role in estimating the injury rate of fishes with high accuracy. Accordingly, the velocity of the conveyor system should be controlled with suitable speed to achieve reliable recognition with the image processing system. The conveyor system in a FSS consists of three or more conveyors, the desired velocities of which are defined as trapezoidal velocity profiles [1]. To control the closedloop dynamics of the conveyor system close to the desired velocities, a system model is used to develop a model-based controller. However, the conveyor system has some uncertain parameters, such as a friction factor, belt elastic factor, pulling force, and others, which are unmeasured in the conveyor system.

An adaptive controller was considered for its important ability to deal with system uncertainties without requiring explicit, unknown plant parameter identification [2][3]. A conventional model reference adaptive controller (CMRAC) tuning control parameters directly is one of the main schemes utilized in the field of adaptive control [4]-[6]. Although asymptotic tracking could be achieved in CMRAC systems, the tracking performance in the transient state could be poor [7] because it is impossible to achieve a small deviation of the tracking error in the transient state with an insufficient adaptation rate.

For engineering systems, it should be noted that the control input signal is frequently saturated and has proved to be a source of performance degradation. An input control signal saturation could lead to poor control performance and even closed-loop system instability [8][9] if its effect is not considered in the design of the controller.

In addition, the estimated parameters in the update laws can be varied smoothly in the presence of bounded disturbances. Therefore, certain modifications [10], such as the dead-zone technique, e-modification, or projection operator were utilized to the modify update laws.

This paper proposes a model reference adaptive control approach, in which the reference model is modified by a feedback of a modeling error signal [11], and applied to the velocity control of the conveyor system in a FSS with uncertain parameters, saturated input, and bounded disturbances. In the presence of bounded disturbance, a σ-modification is utilized in the update laws of the proposed controller to eliminate the drift phenomenon of the control parameters. In addition, an auxiliary error vector [12] is employed to compensate for the error dynamics when input saturation occurs. The experimental results verify the effectiveness and the performance of the proposed controller.

2. System Modeling

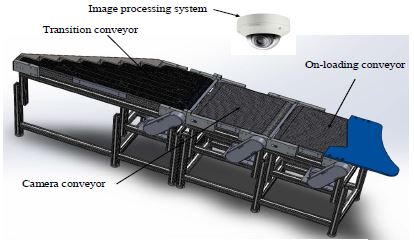
A typical conveyor system in an FSS, as shown in Figure 1, consists of an on-loading conveyor (1st conveyor), a camera conveyor (2nd conveyor) to examine moving fish boxes using an image processing system, and a transition conveyor (3rd conveyor). Each conveyor consists of a mechanical subsystem and an electrical subsystem. The simplified model of the mechanical subsystem of the ith conveyor of the FSS is shown in Figure 2 (i = 1, 2, 3).

Figure 1:

Typical conveyor system in a FSS

Figure 2:

Simplified model of the ith conveyor of FSS

In Figure 2, J_i1 and J_i2 are the moments of inertia of the driving and driven rollers, ω_i1 and ω_i2 are the angular velocities of the driving and driven roller, f_i1 and f_i2 are friction coefficients of bearings inside the driving and driven rollers, and D_i1 and D_i2 are diameters of the driving and driven rollers, respectively.

To simplify the mechanical subsystem modeling, Assumption 1 is proposed as follows:

•　 Assumption 1

√　 The connection between the motor shaft and driving roller is rigid and short.
√　 Belt slippage on the rollers is negligible.
√　 Fish box slippage on the belt is negligible.

The electrical subsystem is used to drive the mechanical subsystem. The inverter with a DC voltage input controls the induction motor to generate sufficient torque to drive the mechanical subsystem, as shown in Figure 2.

Under the above assumptions, the ith mechanical driven system can be expressed by the following:

where J_i = J_i1 + J_i2, f_i = f_i1 + f_i2, τ_di(t) is a bounded external disturbance torque and τ_i is the sufficient torque to drive the mechanical subsystem of the ith conveyor, given as follows:

where k_i is an amplifier gain and u_i^* is the DC voltage input of the ith inverter to create the desired torque τ_i. u_i^* is defined as a saturated control input of the ith conveyor as follows:

where u_i^* is the designed control input for the ith conveyor by the proposed controller, and u_imin and u_imax are the limited thresholds of the ith designed control inputs.

A dynamic FSS based on Equation (1) - Equation (3) can be expressed in the state space as follows:

where x = [ω₁₁ ω₂₁ ω₃₁]^T is an angular velocity output vector of the FSS measured by encoders attached to the driving rollers, ω_i1 is the angular velocity of the driving roller of the ith conveyor, $$ {\mathrm{u}}^{\mathrm{*}}=sat\left(\text{u}\right)={\left[u_1^{*} u_2^{*} u_3^{*}\right]}^T$$ is a saturated control input vector, d(t/)=[d₁ d₂ d₃]^T is a bounded external disturbance vector with $$ d_i=\frac{T_{di}\left(t\right)}{k_i}$$, and the unknown constant matrices A, B∈ℜ^3×3 and a known matrix B_m∈ℜ^3×3 are given as follows: $$ \mathrm{A}=\left[\begin{array}{ccc}{a}_{11}\hfill & 0\hfill & 0\hfill \\ 0\hfill & a_{22}\hfill & 0\hfill \\ 0\hfill & 0\hfill & a_{33}\hfill \end{array}\right]$$, $$ \mathrm{B}=\left[\begin{array}{ccc}{b}_{11}\hfill & 0\hfill & 0\hfill \\ 0\hfill & b_{22}\hfill & 0\hfill \\ 0\hfill & 0\hfill & b_{33}\hfill \end{array}\right]$$ with $$ a_{ii}=-\frac{f_i}{J_i}$$ and $$ b_{ii}=-\frac{k_i}{J_i}$$.

3. Controller Design

The control objective is to determine a designed control input vector u = [u₁ u₂ u₃]^T for a modified model reference adaptive system with saturated inputs and bounded disturbance, such that the angular velocity output vector tracks the output vector of a reference model.

A modified reference model used for its output vector to asymptotically track a trapezoidal-type reference input vector r is chosen as follows:

where λ > 0 is an error feedback gain, x_m = [ω_m1 ω_m2 ω_m3]^T the angular velocity output vector of the modified reference model, ω_mi is the ith reference angular velocity, e is a modeling error vector, r = [r₁ r₂ r₃]^T is the reference angular velocity input vector, and A_m,B_m∈ℜ^3×3 are given as follows:

$$ {\mathrm{A}}_m=\left[\begin{array}{ccc}{a}_{m1}\hfill & 0\hfill & 0\hfill \\ 0\hfill & a_{m2}\hfill & 0\hfill \\ 0\hfill & 0\hfill & a_{m3}\hfill \end{array}\right],{\mathrm{B}}_m=\left[\begin{array}{ccc}{b}_{m1}\hfill & 0\hfill & 0\hfill \\ 0\hfill & b_{m2}\hfill & 0\hfill \\ 0\hfill & 0\hfill & b_{m3}\hfill \end{array}\right]$$

where a_miv, b_mi are reference model parameters chosen to satisfy Assumptions 2 and 3 as follows.

•　 Assumption 2: Given a known Hurwitz matrix A_m∈ℜ^3×3 and a known matrix B_m∈ℜ^3×3 of full rank, there exists an unknown control gain matrix K∈ℜ^3×3 and an unknown positive definite diagonal constant matrix Λ∈ℜ^3×3 such that the following equations hold:

•　 Assumption 3: A positive symmetric definite matrix P = P^T > 0 is the solution of the following Lyapunov equation:

where Q_m is a positive definite matrix.

Substituting Equation (7) into Equation (4), adding and subtracting B_mr, $$ \dot{\text{r}}$$ yields

where Φ = Λ⁻¹, Ω=(B_m/)^-1, and u_r is an ideal control input vector as follows:

The first-order time derivative of e is given by

If u^* = u_r, $$ \dot{\text{e}}\text{=}\left({\text{A}}_m\text{-}\lambda \text{I}\right)\text{e}$$. Because A_m and (A_m-λI) are Hurwitz matrices, it can be concluded that e→0 as t →∞. This implies that the plant in Equation (4) can asymptotically track the reference model in Equation (5). However, the ideal control input vector cannot be implemented, because the matrices K, Φ, and Ω, and the disturbance vector d(t) are unknown. Therefore, a designed control input vector u is chosen as an estimate of u_r in the following form:

where $$ \widehat{\text{K}},\widehat{\text{Φ}},\widehat{\text{Ω}}$$ are estimations of unknown control gain matrices K,Φ,Ω and $$ \widehat{\text{d}}$$∈ℜ³ is an estimated vector of an unknown constant vector $$ \overline{\text{d}}$$, which is the averaged-value vector of d(t) in Equation (4).

A saturated input error vector is defined as

From Equation (10) - Equation (13), the first-order time derivative of e is given as

where $$ \stackrel{\mathrm{~}}{\text{K}}\text{=}\widehat{\text{K}}\text{-K, }\stackrel{\mathrm{~}}{\text{Φ}}\text{=}\widehat{\text{Φ}}\text{-Φ, }\stackrel{\mathrm{~}}{\text{Ω}}\text{=}\widehat{\text{Ω}}\text{-Ω}$$, and $$ \stackrel{\mathrm{~}}{\text{d}}\text{=}\widehat{\text{d}}\text{-d}$$.

To remove the effect of the saturated input, an auxiliary error vector e_Δ is defined as

where (A_m − λI) is a stable Hurwitz matrix and $$ {\widehat{\text{K}}}_{\text{Δ}}\in {\mathfrak{R}}^{3\times 3}$$ is the adaptable parameter matrix.

Therefore, a new error vector is defined as follows:

From Equation (14) ~ Equation (16), the first-order time derivative of e_u is given as

where $$ {\stackrel{\mathrm{~}}{\text{K}}}_{\text{∆}}\text{=}{\widehat{\text{K}}}_{\text{∆}}\text{-}{\text{B}}_m\text{Λ}$$.

The control gains $$ \widehat{\text{K}}\text{,}\widehat{\text{Φ}}\text{,}\widehat{\text{Ω}}\text{,}\widehat{\text{d}}$$ in Equation (12) are estimated by update laws based on a σ-modification that will be designed in Theorem 1.

Theorem 1: An M-MRAC system of Equation (4) is stable as long as a designed control input vector of Equation (12) is given and update laws using a σ-modification are given as

where γ₁, γ₂, γ₃ > 0 are the adaptation rates, and σ is a design parameter.

[Proof of Theorem 1]: A candidate Lyapunov function is chosen to analyze the stability of the system as follows:

The first-order time derivative of V(t) is given as

Using Equation (18) - Equation (20) yields

Using the Rayleigh principle, Equation (23) can be written as follows:

where $$ a_1={\lambda }_{\text{min}}\left({\text{Q}}_m\right)+2{\lambda }_{\text{min}}\left(\text{P}\right)\lambda >0,d_{*}=‖\text{P}{\text{B}}_m\Lambda \left(d-\overline{d}\right)‖\in l_{\infty }, {‖.‖}_F$$ is the Frobenius norm and c is given as follows:

$$ \dot{V}\left(t\right)$$ in Equation (24) is negative semi-definite outside the compact set

This implies that $$ {\text{e}}_u\text{,}\widehat{\text{K}}\text{,}\widehat{\text{Φ}}\text{,}\widehat{\text{Ω}}\text{,}{\widehat{\text{K}}}_{\text{Δ}}\text{, and }\widehat{\text{d}}$$, and $$ \widehat{\text{d}}$$ are bounded from Equations (21), (24), and (26), and 0 e_u → as t →∞ by Barbalat's lemma. Hence, e→e_Δ and e is bounded if and only if e_Δ is also bounded. The boundedness e_Δ is proven as follows:

A candidate of Lyapunov function is chosen as

Using Equations (15) and (27), the first-order time derivative of W is given as

where $$ {\lambda }_3=2‖-{\mathrm{e}}_{\mathrm{\Delta }}^T\text{P}{\widehat{\text{K}}}_{∆}^T\mathrm{\Delta }\text{u}‖\ge 0 \text{and} {\lambda }_2=\frac{a_1}{{\lambda }_{\text{max}}\left(\text{P}\right)}>0.$$

By using the Gronwall–Bellman Inequality, Equation (28) implies that

Using Equations (27) and (29), the following are obtained:

It can be proven that e_Δ is also bounded.

E.O.D

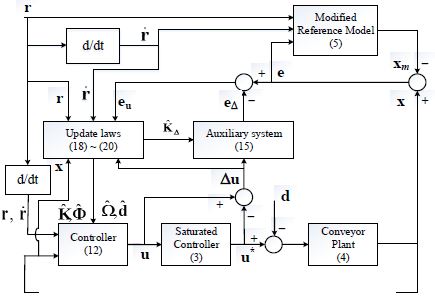
The block diagram of the proposed controller is shown in Figure 3.

Figure 3:

Block diagram of the proposed controller

A comparison of M-MRAC with CMRAC is given in Table 1.

Table 1:

Comparison of M-MRAC with CMRAC

4. Experimental Results

To evaluate the effectiveness of the proposed controller (MMRAC) with σ -modification and compare it with the CMRAC, an experiment was carried out under the following conditions.

The initial values of the state variables and the controller inputs were set to zero. The input voltages of the inverters considered as control inputs of the proposed controller can vary in range from u_1min = u_2min = u_3min = 0 V to u_1max = u_2max = u_3max = 5 V.

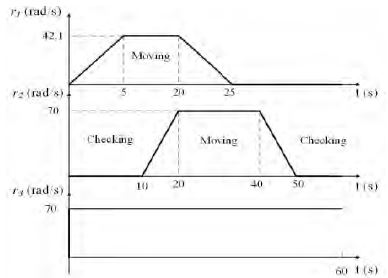
The parameters of the modified model reference system was given by a_m1 = a_m2 = a_m3 = −30 and b_m1 = b_m2 = b_m3 = 30. The error feedback gain was chosen as λ = 10, the fixed controller gains were chosen as γ₂ = 3.3, γ₃ = 1.3, σ = 0.03, and the positive symmetric definite matrix was chosen as P = diag([10^-8 10^-8 10^-8]). The reference inputs for the conveyor plant were the angular velocity inputs and are given in Figure 4.

Figure 4:

Velocity profiles of all conveyors

To demonstrate the effectiveness of the proposed controller, the following three cases were considered.

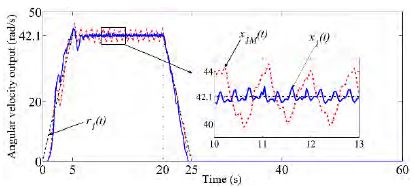
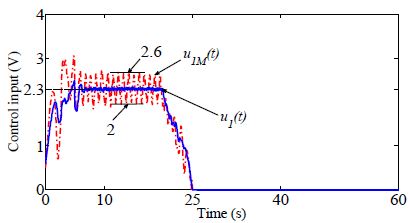
Case 1: The adaptation rates of both the CMRAC and MMRAC are set to γ₁ = 1.67. It can be seen that both the output of the proposed M-MRAC x₁(t) and the output of the CMRAC x_1M(t) for the 1st conveyor track the reference input r₁(t), as shown in Figure 5. However, the output amplitude of the CMRAC varies more strongly than that of the proposed MMRAC. High-frequency oscillations are generated in the control input signal u_1M(t) of the CMRAC, whereas the control input signal u₁(t) of the proposed M-MRAC remains nearly unchanged, as shown in Figure 6, when the angular velocity output reaches 42.1 rad/s in Figure 5.

Figure 5:

Output of the CMRAC and M-MRAC for the 1st conveyor

Figure 6:

Control input of the CMRAC and M-MRAC for the 1st conveyor

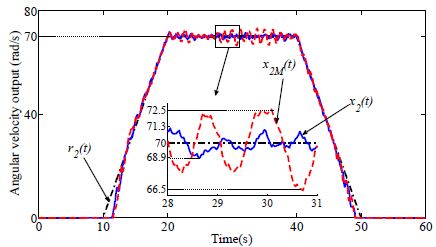
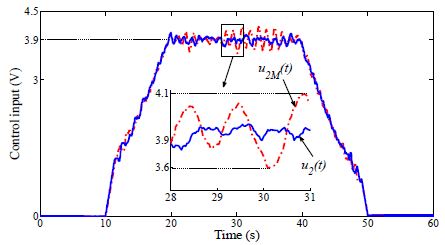
Case 2: The adaptation rates of both the CMRAC and MMRAC are set to γ₁ = 10. The angular velocity output x₂(t) of the proposed M-MRAC for the 2nd conveyor tracks the reference input r₂(t) with a small error (from −1.1 rad/s to +1.3 rad/s), whereas the angular velocity output x_2M(t) of the CMRAC for the 2nd conveyor tracks the reference input r₂(t) with an error from −2.3 rad/s to +2.5 rad/s in Figure 7. The control input u_2M(t) of the CMRAC also oscillates with higher frequency and amplitude than the control input u₂(t) of the proposed M-MRAC, as shown in Figure 8. The maximum and minimum values of the control input of the CMRAC are 4.1 V and 3.72 V, respectively, and the average value of the control input is 3.88 V. The control input for the proposed M-MRAC varies more slowly than that for the CMRAC. Therefore, the performance of the proposed M-MRAC is better than that of the CMRAC in this case.

Figure 7:

Output of the CMRAC and the M-MRAC for the 2nd conveyor

Figure 8:

Control input of the CMRAC and M-MRAC for the 2nd conveyor

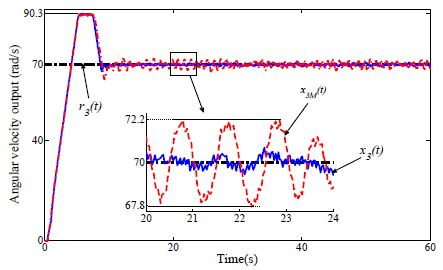
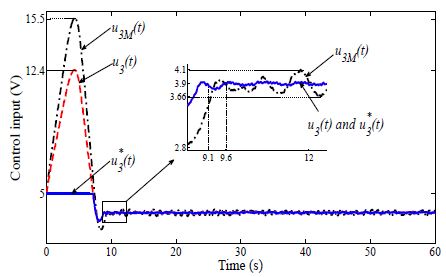
Case 3: Similarly, the adaptation rates of both the CMRAC and M-MRAC are set to γ₁ = 6.67. The angular velocity output x₃(t) of the proposed M-MRAC for the 3rd conveyor also tracks the reference input r₃(t) better than the angular velocity output x_3M(t) of the CMRAC, as shown in Figure 9. Because the reference input r₃(t) is a step type, the control input signal amplitudes of both the proposed M-MRAC and the CMRAC are large (15.5 V and 12.5 V, respectively), as shown in Figure 10. Therefore, the saturated control input u₃^*(t) is set to u_3max = 5 V, and the angular velocity outputs of both the proposed MMRAC and the CMRAC reach 90.3 rad/s in Figure 9.

Figure 9:

Output of the CMRAC and the M−MRAC for the 3rd conveyor

Figure 10:

Control input of the CMRAC and the M−MRAC for the 3rd conveyor

The tracking performance of the proposed M-MRAC controller versus the CMRAC is given in Table 2.

Table 2:

Modeling error of the CMRAC and M−MRAC

5. Conclusion

A modified-model reference adaptive controller for belt conveyors in an FSS with uncertainty parameters, input saturation, and bounded disturbances was proposed. The feedback of the modeling error signal in the proposed MMRAC controller obtained a smaller modeling error than that in the CMRAC. The tracking performance of the proposed M−MRAC showed a better improvement in both the transient and asymptotic states than that of the CMRAC, and the highfrequency elements in the control input signals were reduced in the proposed M−MRAC when the adaptation rate was increased. The error dynamics under the input saturation were compensated by the auxiliary output error. The experimental results showed that the proposed M-MRAC became more effective than the CMRAC when the adaptation rate was large and the error feedback gain was suitably selected.

Acknowledgments

This research was a part of the project titled “Localization of unloading automation system related to Korean type of fish pump,” funded by the Ministry of Oceans and Fisheries, Korea.

References

• S. Thirachai, P. Komeswarakul, U. Supakchukul, and J. Suwatthikul, “Trapezoidal velocity trajectory generator with speed override capability”, International Conference on Control Automation and Systems, p1468-1472, (2010).
• K. J. Astromn, and B. Wittenmark, Adaptive Control, 2nd ed., Dover publication: INC, (2008).
• D. K. Le, and T. K. Nam, “Optimal iterative learning control with model uncertainty”, Journal of the Korean Society of Marine Engineering, vol. 37(no. 7), p743-751, (2013). [https://doi.org/10.5916/jkosme.2013.37.7.743]
• V. T. Duong, J. H. Jeong, N. S. Jeong, M. S. Shin, T. T. Nguyen, G. S. Byun, and S. B. Kim, “Cross-coupling synchronous velocity control for an uncertain model of transformer winding system using model reference adaptive control method”, Lecture Notes in Electrical Engineering, vol. 371, p441-455, (2016).
• T. T. Nestorovic, H. Koppe, and U. Gabbert, “Direct model reference adaptive control (MRAC) design and simulation for the vibration suppression of piezoelectric smart structures”, Communications in Nonlinear Science and Numerical Simulation, vol. 13(no. 9), p1896-1909, (2008).
• S. Karason, and A. Annaswamy, “Adaptive control in the presence of input constraints”, IEEE Transactions on Automatic Control, vol. 39(no. 11), p2325-2330, (1994). [https://doi.org/10.1109/9.333787]
• D. J. Wagg, “Transient bounds for adaptive control systems”, IEEE Transactions on Automatic Control, vol. 39(no. 1), p171-175, (1994).
• D. Y. Abramovitch, and G. F. Franklin, “On the stability of adaptive pole-placement controllers with a saturating actuator”, IEEE Trans. on Automatic Control, vol. 35(no. 3), p303-306, (1990). [https://doi.org/10.1109/9.50341]
• W. Sun, H. Gao, and O. Kaynak, “Vibration isolation for active suspensions with performance constraints and actuator saturation”, IEEE/ASME Transactions on Mechatronics, vol. 20(no. 2), p675-683, (2015). [https://doi.org/10.1109/tmech.2014.2319355]
• V. Stepanyan, and K. Kalmanje, “Input and output performance of M-MRAC in the presence of bounded disturbances”, AIAA Guidance, Navigation, and Control Conference, p2-5, (2010). [https://doi.org/10.2514/6.2010-7688]
• T. Gibson, A. Annaswamy, and E. Lavretsky, “Adaptive systems with closed–loop reference models, Part I: Transient performance”, American Control Conference, p3376-3383, (2013).
• V. T. Duong, T. H. Nguyen, T. T. Nguyen, J. M. Lee, and S. B. Kim, “Modified model reference adaptive controller for a nonlinear SISO system with external disturbance and input constraint”, Lecture Notes in Electrical Engineering, vol. 415, p118-128, (2016).