자기벡터기반 최대우도추정법을 이용한 실내위치측위 연구

2.1 지자기기반 자기벡터특성

지구의 남극에 N극이 위치하고 북극에 S극이 위치하여 지구 전체를 감싸는 자기장을 지자기장이라 한다. 지구의 자력선 방향은 남극의 N극에서 북극의 S극으로 흐르며 남극의 N에서 상향, 북극의 S극에서 하향, 적도를 중심으로 수평으로 위도에 따라 다르게 분포 한다[11].

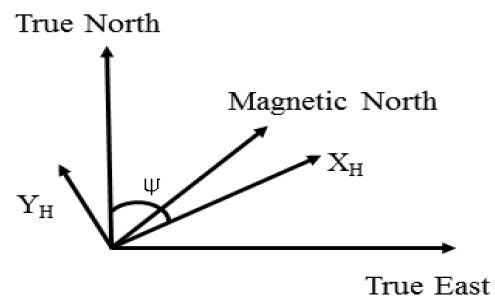
지자기장의 크기는 매우 작기 때문에 지자기 센서 주변의 물체 및 환경의 영향에 의해 왜곡 발생이 쉬우며 방위각의 오차를 유발시킨다. Figure 1은 수평 좌표계 상에서 평면 자기벡터와 방위각의 상호 관계를 나타낸 것이다. 방위각은 3축 지자기를 측정하여 이를 현재 자세에 대한 수평좌표계로 변환한 후 획득한 평면 자기벡터를 이용하여 계산하며 식 (1)과 같다.

Figure 1:

Correlation between plane Magnetic vector and Azimuth angle

여기서, X_H와 Y_H는 각각 평면 자기벡터성분이고 mx, my, mz는 각 축의 지구자기장이다. ϕ와 θ는 각각 Roll, Pitch의 자세 각이고, Ψ는 기준좌표계에 대한 방위각이다. 지자기 센서를 이용하여 실내에서 지구자기장을 측정할 경우 센서에 영향을 줄 수 있는 자성 물체 및 건축구조와 동작 환경에 따라 측정값의 왜곡이 발생할 수 있다[13]-[15].

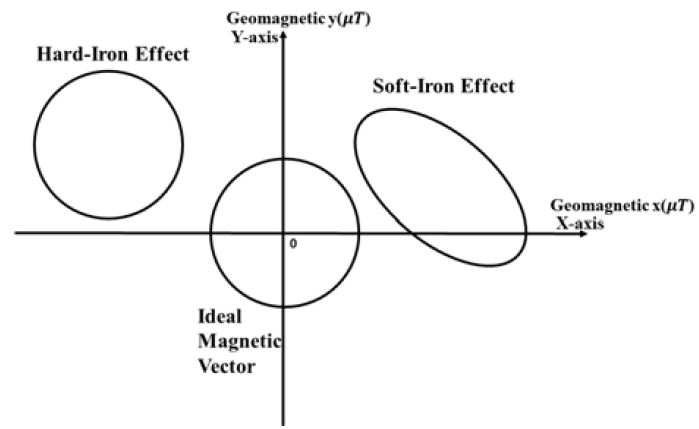
지자기 센서를 yaw축을 중심으로 0°~360°로 회전시킨 지자기 x값과 지자기 y값을 그래프 상에 출력시키면 Figure 2와 같은 수평 자기벡터특성이 나타난다. Figure 2의 x축은 지자기 x값이며 y축은 지자기 y값을 의미하며 Ideal Magnetic Vector는 주변에 자기 왜곡이 없는 이상적인 자기 벡터특성이다. Hard-Iron Effect는 센서 주변의 자성 물체 및 건물 구조를 이루는 철골 등에 의하여 왜곡이 생긴 특성으로 이상적인 자기벡터와 같이 원의 형태를 이루고 있으나 좌표 상 중점이 이동된다. Soft-Iron Effect는 지자기 센서 내부에 철과 니켈 등의 재료들이 전기적인 신호를 받아 자기장을 형성함으로서 왜곡이 발생하는 특성으로 타원의 형태로 출력되는 특성이다. 이러한 위치 별 왜곡 특성 분석을 기반으로 위치 구분이 가능하다.

Figure 2:

Magnetic vector

2.2 최대우도추정법

최대우도추정법은 어떤 확률변수에서 표집한 값들을 토대로 그 확률변수의 모수를 구하는 방법으로 어떤 모수가 주어졌을 때 원하는 값들이 나올 가능도를 최대로 만드는 모수를 선택하는 방법이다. 확률벡터 X_d 가 모수벡터가 μ 와 Σ인 다변수 정규분포(Multivariate Normal distribution, MVN)를 따른다고 할 때 X_d는 X의 d x 1벡터, μ 는 d x 1벡터, Σ는 d x d 행렬이 된다.

이러한 다변수 정규분포의 확률밀도함수(Probability Density Function)는 식 (3)과 같다.

x_i는 i개의 표본 값을 의미하며 n개의 샘플 사이즈를 가정할 경우 우도함수(Likelihood function)는 식 (4)와 같이 나타낸다.

양변에 로그 함수를 취하여 로그우도함수(Loglikelihood function)를 도출하면 식 (5)와 같다.

최대우도추정연산은 로그우도함수를 최대로 만드는 μ와Σ의 값을 구하는 것이므로 식 (6)과 같이 모수와 관계없는 첫 번째 항을 생략해도 구하고자 하는 값은 동일하다.

본 연산을 통해 위치인식을 위한 공간에서 생성한 DB와 수집되는 값과의 위치 별 최대가능도 비교가 가능하며 오차거리를 줄일 수 있다.

3.1 시스템 구성

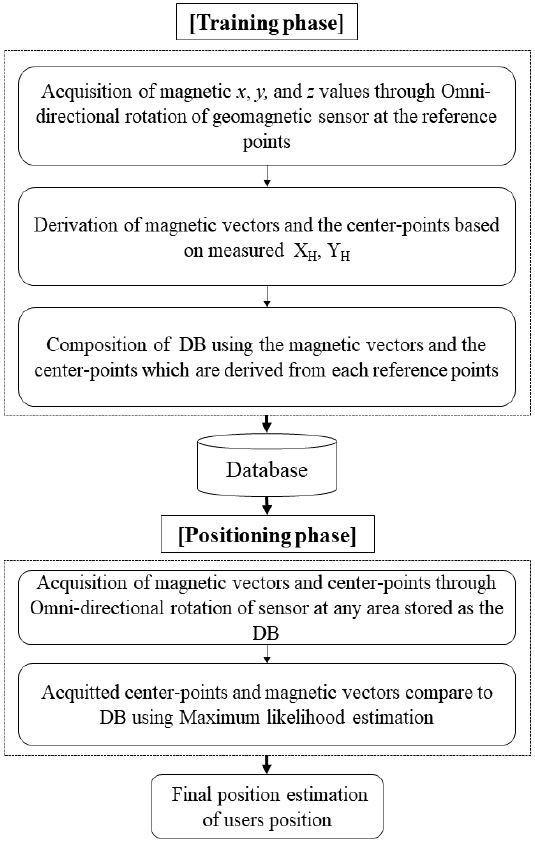
제안하는 시스템은 Figure 3으로 실내공간에서 Wi-Fi, 블루투스 등의 WLAN환경에서 가장 많이 쓰이는 실내위치추정 방법인 Fingerprint를 기반으로 위치정보를 DB에 저장하기 위해 일정한 간격으로 설정한 참조위치(Reference point)를 기준위치로 잡는다. 그 위치에서 센서의 신호를 수집하여 DB를 구성 하는 Training phase와 구성된 DB와 비교를 통해 실시간으로 센서에 측정되는 신호 값을 이용하여 위치를 추정하는 Positioning phase로 진행한다. Training phase에서 방위가 변하더라도 위치인식을 위한 공간에서 다수의 기준위치 당 동일한 yaw축에서 지자기센서를 0°~350° 전방향으로 회전시켜 수집되는 지자기 x, y, z값을 획득한다. 획득된 지자기 값을 기반으로 식 (1)을 적용하여 타원의 형태로 출력되는 자기벡터성분인 X_H와 Y_H를 획득하고 그 중점을 DB로 저장한다.

Figure 3:

The positioning system architecture by proposed algorithm

Positioning phase에서 위치 인식을 위한 지점에서 지자기 센서의 0°~360° 전 방향 회전을 통해 수집되는 지자기 x, y, z값에 따른 자기벡터를 획득하고 그 중점을 DB와 비교한다. 이 때 획득하는 자기벡터성분인 지자기 x, y값, 중점좌표 x, y를 센서 회전을 통해 위치 당 각도에 따라 수집 가능하며 최대우도추정연산을 통해 수집되는 값들을 DB와의 위치추정확률을 향상시켜 위치를 인식한다.

3.2 자기벡터특성의 파라미터 도출

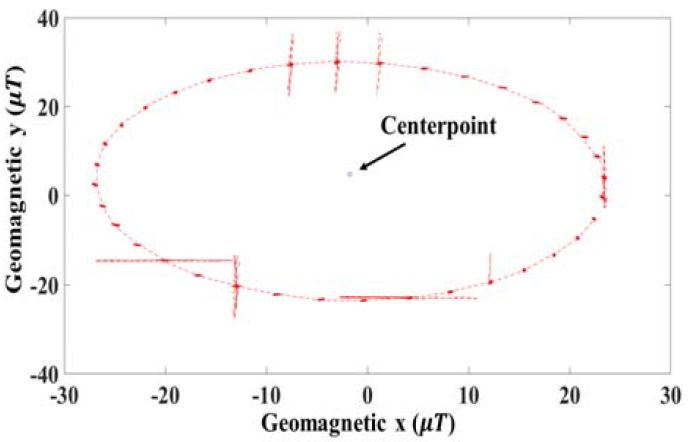
위치측위 시 임의의 위치에 방위각에 따른 자기벡터의 중점을 얻기 위하여 0°~360° 전방향에 대하여 지자기 x, y, z 값을 수집한다. 식 (1)에 따라 연산을 하여 X_H, Y_H를 도출하여 그래프 상에 출력시키면 Figure 4와 같이 타원의 형태로 출력되는 특성이 나타난다. 다음과 같이 타원의 형태로 출력되는 자기벡터특성은 지자기의 왜곡 현상에 의해 발생하며 식 (7)의 연산을 통해 중점 획득이 가능하다. max(m_x ) 는 X_H의 최댓값, min (m_x )는 X_H의 최솟값으로 두 값의 중심을 중점 x좌표인 Centerpoint_x로 Y_H의 최댓값인 max(m_y )와 Y_H의 최솟값 min (m_y )의 중심을 중점 y좌표인 Centerpoint_y로 도출하여 타원의 중점 좌표 Centerpoint를 획득한다.

Figure 4:

The centerpoint of magnetic vector

3.3 최대우도추정법을 이용한 위치정보 파악

본 시스템에서는 센서로부터 획득한 기준위치 당 자기벡터와 그 중점에 대한 평균벡터 M을 저장하기 위해 다음의 식 (8)을 이용한다.

여기서, X_i는 기준위치 당 수집되는 자기벡터 및 그 중점과 DB를 비교하여 얻은 값이며 i는 기준위치 개수다. n은 해당 위치 별 자기벡터와 중점의 수집데이터 개수이며 M_{1 : p}는 p개 위치를 가진 평균벡터다. M_{1 : p}는 MX_H, MY_H, MCP_x, MCP_y로 이루어진 벡터이며 MX_H와 MY_H는 자기벡터성분인 X_H, Y_H이며 그 중점좌표에서 x좌표 MCP_x, y좌표 MCP_y로 나타낸다.

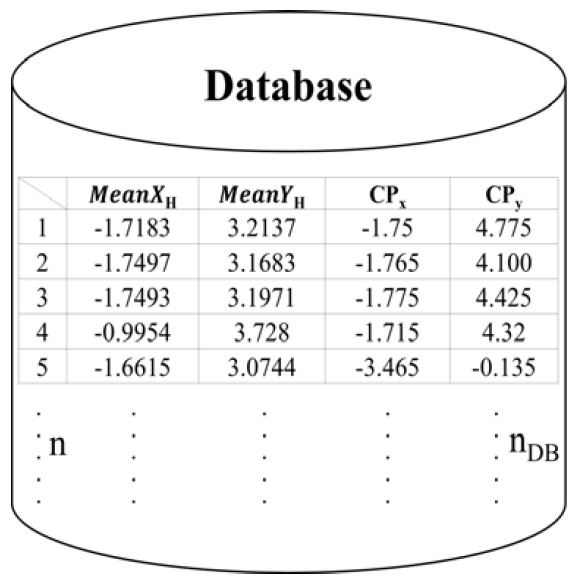
제안하는 시스템에 따른 DB를 Figure 5에 나타내었다. MeanX_H와 MeanY_H는 n개의 기준위치 당 자기벡터 성분인 X_H, Y_H를 전방향 각도에 따른 값들을 평균을 낸 값이고 CP_x와 CP_y는 중점좌표의 값으로 n_DB개 구축한 것이며 이를 식 (9)에 DB정보로 사용한다.

Figure 5:

The proposed database

여기서, DBX_{H(i )}, DBY_{H(i )}는 MeanX_H, MeanY_H값이고 DBCp_{x(i )} , DBC p_{y(i )}는 CP_x, CP_y값이다. X_{H(i )}, Y_{H(i )}, Cp_{x(i )}, Cp_x(i)는 각 위치에서 각도별 X_H, Y_H, CP_x, CP_y의 값이다. DBX_{H(i )}, DBY_{H(i )}, DBC p_{x(i )}, DBCp_{y(i )}와 n개를 1개씩 순서대로 비교한 후 이로부터 획득된 평균벡터를 식 (10)에 적용한다.

여기서, 위치별 수집되는 자기벡터 및 그 중점들의 추정 값을 획득하기 위해 기준위치에서 수집되는 값 x_i를 DB의 모수벡터 μ와 수집 개수 m개씩 비교하였다. x_i와 μ는 $$ {LX}_{H_{1:p}},{LY}_{H_{1:p}},{LCP}_{H_{1:p}},{LCP}_{H_{1:p}}$$의 4개의 요소에 의해 위치 확률을 찾으며 연산 시 $$ {LX}_{H_{1:p}},{LY}_{H_{1:p}},{LCP}_{H_{1:p}},{LCP}_{H_{1:p}}$$는 각각 기준위치 당 자기벡터 성분인 X_H, Y_H와 중점좌표 CP_x, CP_y의 위치확률로 DBX_{H(i )}, DBY_{H(i )}, DBC_{px(i )}, DBC_{py(i )}를 μ의 값으로 각각 대입하여 전체 위치 확률을 찾는다.

4.1 알고리즘 적용을 위한 실험환경

본 논문에서는 DB 구축 및 위치인식을 위해 Figure 6 (a)에 3축 가속도, 각속도, 지자기, 온도, 자세 및 방향 정보를 제공하는 mySen-C AHRS센서를 이용하여 x, y, z축 지자기 값을 측정하였다.

Figure 6:

The AHRS sensor and module used for experiment and experimental condition

해당 센서의 자세한 스펙은 Table 1과 같으며 100Hz의 빠른 데이터 출력 속도를 가지므로 사용 환경에 따라 유연하게 적용 가능한 옵션설정을 지원한다. 본 논문에서는 초당 100개를 수집함에 따라 위치측위 시 수집 개수에 따른 오차 거리 및 정확도를 분석하였으며 최적의 수집 개수를 결정하여 결과 도출하였다.

Table 1:

mySen-C Specification

실험 장소는 책상과 장애물로 이루어진 일반적인 실내 공간에서 위치정확도를 파악하기 위해 한국해양대학교 공과대학 1호관 2층 전기전자실험실을 선정하였다.

실험 장비구성은 센서 회전을 위해 Figure 6 (b)와 같이 아두이노와 스테핑모터를 모듈화 하였으며 스테핑모터의 상부중앙부분과 센서의 중심축을 고정하여 yaw축에 대하여 원하는 방위각에 따라 정확한 회전을 가능하도록 하였다.

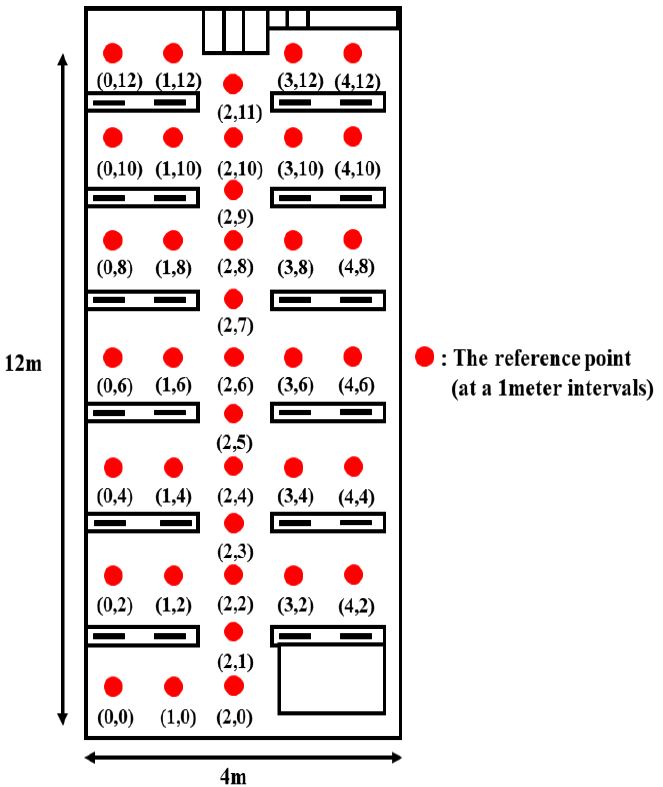
실제 실험측정위치는 Figure 6 (c)의 4 m x 12 m 공간에서 사람의 이동 간격을 1m로 가정하여 Figure 7과 같이 기준위치를 1m로 설정하였으며 측정거리 1m, 높이 1m의 간격으로 38개 위치 당 센서를 전방향에 대해 회전시켜 0°~350°의 36개 방위각에서 10° 단위로 500회씩 x, y, z축 지자기 값을 수집하였다.

Figure 7:

Collection of geomagnetic signal through the sensor

기존 지자기세기 기반 DB 구축 방식은 기준위치 당 한각도에서 DB를 구축하기 때문에 전방향 방위각에 대한 지자기 값을 포함하지 않는다. 제안하는 방식은 기준위치 당 전방향 방위각의 지자기 값을 포함하여 기준 방식 대비 시간이 소요되지만 방위각이 변화하더라도 위치인식 정확도가 개선되었다.

획득한 지자기 값을 식 (1)의 연산을 적용하여 자기벡터를 얻고 그 값을 기반으로 식 (7)의 연산을 적용하여 각 위치 당 자기벡터의 중점을 도출하였으며 최대우도추정연산을 위하여 식 (9)에 기준위치 개수 p = 38, 획득개수 n = 500으로 적용하여 샘플평균벡터 refposi_{1 : 38} 를 생성하였다. 생성된 샘플평균벡터의 따른 수집개수 m결정과 그에 따른 분석 및 위치추정결과를 설명한다.

4.2 실험 결과

생성된 샘플평균벡터를 식 (10)에 대입하기 위해 위치 정확도와 평균거리오차를 도출할 수 있는 수집개수 m을 결정한 실험 결과는 Table 2와 같다.

Table 2:

Determination of m according to accuracy and positioning time

여기서, m은 수집 개수이며 Accuracy는 정확도, Mean error distance는 평균오차거리, Positioning time은 위치인식 시 임의의 위치에서 지자기 x, y, z값의 수집시간과 자기벡터와 그 중점을 도출하여 위치를 추정하는 연산시간이며 a는 최대 정확도인 m = 250과 m = 500을 기준으로 각각의 m을 백분율로 나타낸 것이고 b는 최소 위치인식시간인 m = 5를 기준으로 각각의 m을 백분율로 나타낸 것이며 c는 a와 b의 벡터 크기 값으로 m = 10일 경우에 130.44로 최적의 m을 결정하였다. 이에 따라 식 (10)의 수집 개수 m을 10으로 결정하고 위치인식 시 위치 당 지자기 x, 지자기 y, 중점 x, 중점 y값을 10개씩 수집하고 DB와 비교하여 각 위치별 최대우도추정연산을 하였다.

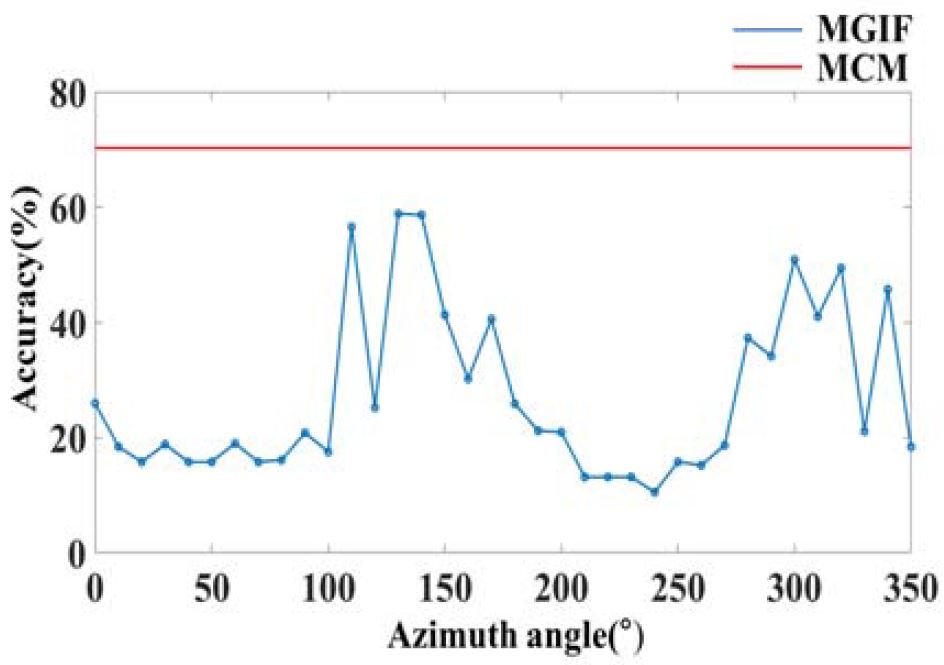
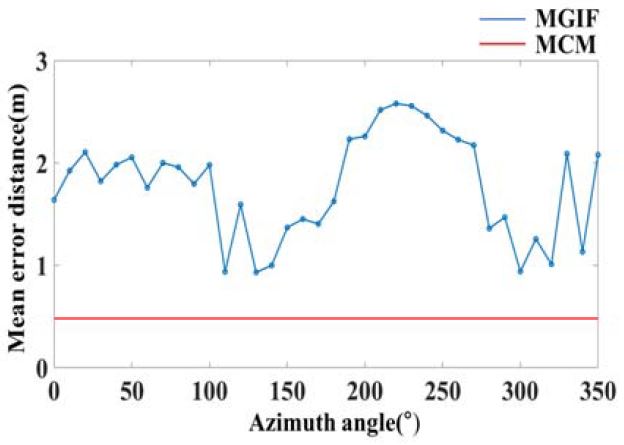
Figure 8과 Figure 9는 각각 0°~350° 전방향에 대해 각도에 따른 위치별 정확도와 평균오차거리를 나타낸 그래프로 x축은 0°~350° 전방향 각도, y축은 정확도를 의미한다. 기존 Fingerprint기반 지자기 위치인식 방식(Using Magnitude of the Geomagnetic Intensity based Fingerprint: MGIF)은 파란 실선과 점으로 표현하였다. 위치별 정확도와 평균오차거리를 보면 0°~100°까지는 유사한 x, y, z축 지자기 값의 각 벡터별 크기의 합에 의해 동일한 부분으로 인식하여 오차가 발생하고 평균오차거리가 가장 큰 210°~260°는 위치별 정확도에서 가장 낮은 정확도를 가지며 평균정확도 27.146 %, 평균오차거리 1.778 m로 방위각이 변화함에 따라 오차 범위가 다양하게 분포되어있다.

Figure 8:

Position accuracy from 0° to 350° degrees in all directions

Figure 9:

Position mean error distance from 0° to 350° degrees in all directions

제안하는 알고리즘(Using Magnetic vector and Centerpoint based Maximum likelihood estimation: MCM)의 결과는 빨간 실선으로 표현하였다. Figure 8과 Figure 9에서 제안하는 방법을 각도에 따라 점으로 표현하지 않은 이유는 DB와 실시간으로 수집되는 전방향 자기벡터 및 중점 값만을 비교하기 때문에 각도에 의한 정확도와 오차를 구분하기 어렵다. 센서 내재적 오차가 존재함에도 불구하고 동일한 위치에서 방위각이 변화하더라도 70.315 %의 정확도와 평균오차거리 0.4817 m로 위치인식의 성능을 검증하였다.

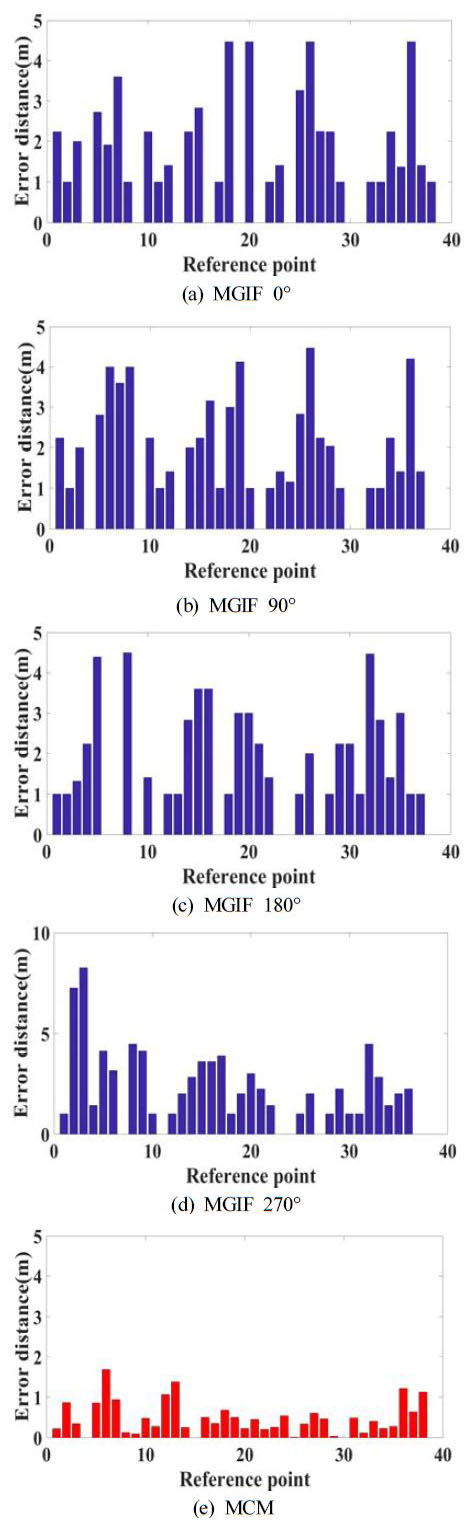
Figure 10 (a) ~ Figure 10 (d)는 MGIF 방식을 이용하여 0°, 90°, 180°, 270°의 각도에서 위치별 오차거리를 나타낸 것이고 Figure 10 (e)는 MCM 방식의 위치별 오차거리를 나타낸 것으로 x축은 38개의 기준 위치고 y축은 오차거리다. Figure 10에 위치를 인식하는 오차거리 0 m를 제외한 Figure 10 (a)는 평균오차거리 1.639 m로 2, 8, 11, 17, 22, 29, 32, 33, 38번째 위치에서 최소오차거리 1 m이며 18, 20, 26, 36번째 위치에서 최대오차거리 4.472 m다. Figure 10 (b)는 평균오차거리 1.796 m로 2, 11, 17, 20, 22, 29, 32, 33번째 .위치에서 최소오차거리 1 m이며 26번째 위치에서 최대오차거리 4.472 m다. Figure 10 (c)는 평균오차거리 1.625 m로 1, 2, 12, 13, 18, 25, 28, 31, 36, 37번째 위치에서 최소오차거리 1 m이며 8번째 위치에서 최대오차거리 4.504 m다. Figure 10 (d)는 평균오차거리 2.173 m로 1, 10, 12, 18, 25, 28, 30, 31번째 위치에서 최소오차거리 1 m이며 3번째 위치에서 최대오차거리 8.246 m다. Figure 10 (e)는 평균오차거리 0.482 m로 25번째 위치에서 최소오차거리 0.02 m이며 6번째 위치에서 최대오차거리 1.689 m다. Figure 10 (a) ~ Figure 10 (d)는 x, y, z축의 지자기 값의 각 벡터별 크기의 합을 이용하여 위치를 인식하기 때문에 위치인식을 하고자 하는 공간에서 전방향 방위각에 따라 동일한 크기의 값이 분포하여 오차가 발생한다. Figure 10 (e)은 x, y, z축의 지자기 값의 자기벡터를 획득하고 그 중점을 사용함으로써 방위각이 변화하더라도 오차에 강인함을 보였으며 다음의 분석을 기반으로 알고리즘에 따른 결과를 Table 3에 나타내었다.

Figure 10:

Position error distance using MGIF 0°, 90°, 180°, 270° degrees in all directions and MCM

Table 3:

Comparison of MGIF and MCM

4 m x 12 m 실내공간에서 0°~350° 전방향에 대한 위치인식 결과로 기존 방법인 Fingerprint기반 x, y, z축의 지자기값을 획득하여 각 벡터별 크기의 합을 이용하여 DB를 구성하고 수집되는 값과 비교하는 방식은 최소 오차거리 1 m, 최대 오차거리 8.246 m, 평균 오차거리 1.778 m, 정확도 27.146 %로 나타난다. 제안하는 방법은 x, y, z축 지자기 값의 자기벡터와 그 중점을 찾아 DB를 구성하고 위치인식시 센서를 회전시켜 수집되는 자기벡터 그 중점을 DB와 최대우도추정연산을 통해 위치인식 하는 방식으로 최소 오차거리 0.02 m, 최대 오차거리 1.689 m, 평균 오차거리 0.482 m, 정확도 70.315 %로 방위각에 변화에 따라 위치인식에 개선된 결과를 보였다.