단상 모델을 이용한 알루미나/물 나노유체 열전달 특성에 관한 수치해석
Copyright ⓒ The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
본 연구에서는 단상 모델 접근법을 이용하여 나노유체의 열전달 특성에 관한 수치해석적 연구를 수행하였다. 수치해석은 기존에 수행된 실험적 연구를 기반으로 진행되었다. 나노유체는 직경 10-20nm의 0.5vol%, 1.0vol% 알루미나/물이며, 길이 1m, 내경 7mm 원관에서의 열전달 특성을 분석하였다. 원관 벽면에 일정한 열유속 9000W/m2가 적용되었으며, 레이놀즈수 470에서 1900 범위에서 수행되었다. 입구 측에서는 높은 열전달 계수가 나타났으며, 출구 측으로 갈수록 열전달 계수는 감소하였다. 그리고 레이놀즈수가 증가할수록 열전달 계수는 증가하였다. 전반적으로 수치해석에 의한 결과는 실험 결과를 잘 예측하였다. 1vol%의 나노유체에서 열전달 계수는 물에 비해서 최대 15% 증가하였다.
Abstract
A numerical study on the heat transfer characteristics of nanofluid was conducted using a single-phase model. The numerical analysis was performed based on a previous experimental study. The nanofluids were Al2O3/water with particle sizes of 10 to 20 nm and particle concentrations of 0.5 and 1 vol%. The heat transfer characteristics were analyzed in a tube having a length and inner diameter of 1 m and 7 mm, respectively. A constant heat flux of 9000 W/m2 was applied at the tube wall, and the Reynolds number ranged from 470 to 1900. Consequently, high heat transfer coefficients were obtained at the inlet region. The heat transfer coefficients decreased as the nanofluid flowed to the outlet region, but increased as the Reynolds number increased. The numerical results generally agreed with the experimental results. The heat transfer coefficient of the nanofluid with 1.0 vol% increased up to 15%.
Keywords:
Computational fluid dynamics (CFD), Nanofluid, Alumina, Heat transfer coefficient, Thermal conductivity, Single phase model키워드:
전산유체역학, 나노유체, 알루미나, 열전달 계수, 열전도도, 단상 모델1. 서 론
에너지 관리의 측면에서 공학자들은 계속해서 ‘보다 효율적인’ 시스템 개발에 많은 노력을 기울이고 있으며, 이러한 노력에 힘입어 시스템 내 각종 장비들의 효율 개선에 새로운 개념의 많은 공학적 도전이 이루어지고 있다. 그 중 일부는 현재까지도 지속적으로 연구되고 있으며 또한 효과적으로 활용되고 있다.
높은 열효율을 얻기 위한 방법 중 하나인 나노유체(nanofluid)는 Choi and Eastman[1]에 의해 제안되었으며, 기반유체(base fluid)에 100nm 이하의 크기를 가지는 고체 나노입자를 분산시켜 열전달 유체로 활용하여 높은 열전달 성능을 얻는 방법이다. 열교환기에서 열전달 성능의 향상은 같은 양의 열 교환을 위해서는 적은 양의 냉매를 필요로 하며, 이것은 곧 장비 사이즈의 축소와 제작 단가의 감소를 가져온다.
일반적으로 유체는 금속과 비교해서 매우 낮은 열전도도를 가진다. 따라서 유체에 금속 입자를 첨가하여 기존의 유체의 열전달 성능을 향상시키는 아이디어는 이미 오래전에 제안되었다. 하지만 밀리미터, 마이크로미터 크기의 입자는 유로 내에서 응집, 침강, 침식 그리고 구동 부위에서의 마모 등의 문제를 야기하였다[2][3].
이에 반해서, 나노입자는 그 크기가 분자 스케일에 접근해 감으로써 중력의 작용에 크게 영향을 받지 않으며, 분자의 무작위 운동인 브라운 운동에 의해 유체 내에서 부유하게 되어, 높은 소산 안정성을 갖는다[4][5]. 또한 입자와 유체 간 열전달 면적이 증가하므로 높은 유효 열전도도를 가지며, 기존의 큰 입자의 슬러리 상태의 열전달 유체와 비교해서 입자에 의한 막힘 현상이 적기 때문에 마이크로 시스템에서도 충분히 활용될 수 있다. 또한 입자의 농도 변화에 따라서 나노유체의 물성치를 조절할 수 있기 때문에 다양한 상황에 적절하게 적용될 수 있는 장점이 있다. 나노 유체는 현재 주로 두 가지 방법(one-step method, two-step method)에 의해서 제작되는데[6], 이 때 나노 입자의 분산이 충분히 이루어 지지 않으면 나노 입자의 응집 현상이 발생할 수 있다.
Wen and Ding[7]은 0.6, 1.0, 1.6 vol%의 Al2O3/water 나노유체에 대해서 Reynolds number 500-2100 범위에서 수평 원관에서의 열전달 특성에 대해서 실험적 연구를 수행하였다. 입자 농도와 Reynolds number의 증가에 따라서 열전달 계수는 증가하였으며, 또한 입구 영역에서 높은 열전달 계수가 나타났으며, 출구 영역으로 갈수록 열전달 계수는 감소하였다. 또한 대류 열전달 계수의 증가의 주요 원인으로 유효 열전도도의 상승뿐만 아니라 입자 운동에 의한 열 경계층 두께가 감소되는 메커니즘을 제안하였다.
Esmaeilzadeh et al. [8]은 평균 직경 15nm의 Al2O3 나노입자와 기반유체로서 물을 사용한 나노유체의 열전달, 유체역학적 특성에 대한 실험을 진행하였다. 체적 분율의 변화에 따른 열전달 계수와 마찰 계수를 분석하였으며, 0.5vol%와 1 vol%의 체적 분율에 대해서 높은 체적 분율에서 열전달 향상은 더 크게 나타났으며, 마찰 계수는 기반 유체와 비교해서 큰 변화가 없는 것으로 나타났다.
Kim et al. [9]은 50nm 이하의 Al2O3/water의 나노유체를 사용하여 실험적인 연구를 진행하였다. 내경 4.5mm, 길이 1m의 동관의 시험부에 입자 농도 2, 4, 6 wt% 와 Reynolds number 500-1700 조건에서 실험을 수행하였다. 높은 입자 농도(6 wt%)에서 가장 높은 열전달 계수가 나타났으며, 물과 비교해서 최대 37-46%의 열전달 계수의 향상이 발견되었다.
실험적 연구들을 기반으로 최근에는 수치해석적 연구들도 진행되고 있다. 수치적 연구는 주로 단상 모델(single-phase model)과 2상 모델(two-phase model) 두가지 방법을 사용하여 진행된다. 나노유체는 기반 유체와 나노 입자가 혼합된 형태로 다상(multi-phase) 유동으로 취급해야 하지만, 나노 입자는 기반 유체에 잘 혼합되어 쉽게 열적 평형 상태에 이를 수 있으므로 균질류 모델(homogeneous model)인 단상 모델로 접근할 수 있다. 이것은 기반 유체와 나노 입자의 평균적인 물성치를 가지는 단상의 유체로서 가정되며, 그 결과 두 상은 같은 압력장과 속도장을 가지는 것으로 취급된다.
Moraveji et al. [10]은 수평 원관에서 Al2O3/water 나노유체의 열전달 특성에 대한 수치적 연구를 수행하였으며, 단상 모델을 사용한 수치해석의 결과는 Anoop et al. [11]의 실험결과와 비교되었다. 작은 직경을 가지는 나노유체에 대해 높은 Reynolds number 범위에서 수치해석과 실험 결과는 잘 일치하는 것을 보였다.
Behroyan et al. [12]는 난류 강제 대류에서의 Cu/water 나노유체에 대해서 2종류의 단상 모델과 3종류의 2상 모델을 사용하여 수치해석을 수행하였다. 수치해석 결과는 Xuan and Li [13]의 실험결과와 비교, 분석 되었다. 수치해석 결과에 따르면 단상 모델은 비뉴턴유체 단상 모델 보다는 뉴턴유체 단상 모델이 정확성이 높았으며, 2상 모델은 혼합모델(mixture model)과 오일러-오일러 모델(Eulerian-Eulerian model)보다 오일러-라그랑지 모델(Eulerian-Lagrangian model)이 정확성이 높게 나타났다. 따라서 나노 유체를 해석하기 위해서 뉴턴유체 단상 모델과 오일러-라그랑지 2상 모델을 추천하였다. 실험적인 연구에 비해서 수치해석적인 연구는 부족한 실정이다. 수치해석 기법의 발달로 나노유체의 열전달 및 유동 특성에 대한 정확한 예측이 가능해진다면, 실용적인 측면은 물론이며, 실험적인 측면에서 많은 노력과 시간이 단축될 것으로 보인다.
본 연구에서는 뉴턴유체 단상 모델을 사용하여 수치해석을 수행하였으며, 수치해석은 CFD 상용코드 중 하나인 CFX 13.0을 사용하였다. Esmaeilzadeh et al. [8]의 실험 결과와 비교하여 신뢰성을 확보하였다. 또한 수치해석을 수행하기 위해서 여러 상관식을 이용하여 나노유체의 열전도도를 계산하였으며, 열전도도 상관식에 따른 열전달 계수를 분석하였다.
2. 수치해석
2.1 단상 모델링
뉴턴유체, 정상 유동에 관한 지배 방정식은 다음 식들과 같이 표현된다.
| (1) |
| (2) |
| (3) |
식 (1) ~ 식 (3)은 각각 연속 방정식, 운동량 방정식 그리고 에너지 방정식이며, 여기서 ρ와 는 각각 밀도와 속도를 의미한다. 그리고 P는 압력, μ는 점성계수, SM는 소스항으로서 여기서는 체적력을 포함하며, T는 온도를 의미한다. cp는 정압비열을 뜻하며, 하첨자 nf는 나노유체를 나타낸다.
나노유체의 밀도는 식 (4)와 같이 계산된다.
| (4) |
여기서 ϕ는 입자의 체적 분율을 나타내며, 하첨자 bf와 p는 각각 기반 유체와 나노입자를 의미한다.
단위 체적당 열용량은 다음과 같이 계산된다.
| (5) |
점성계수는 식 (6)과 같이 Einstein[14]의 상관식을 이용하여 계산하였다.
| (6) |
본 연구에서는 나노유체의 열전도도, knf의 예측에 따른 열전달 특성을 고려하기 위해서 3가지 상관식을 사용하여 비교하였다. 식 (7) ~ 식 (9)는 각각 Maxwell[15], Maiga et al. [16] 그리고 Prasher et al. [17]에 의해서 제안된 상관식이다.
| (7) |
| (8) |
| (9) |
식 (9)에서 A와 m은 상수로서 여기서는 각각 40000과 2.5이며, Re 와 Pr은 각각 Reynolds number와 Prandtl number를 의미한다.
2.2 해석 조건
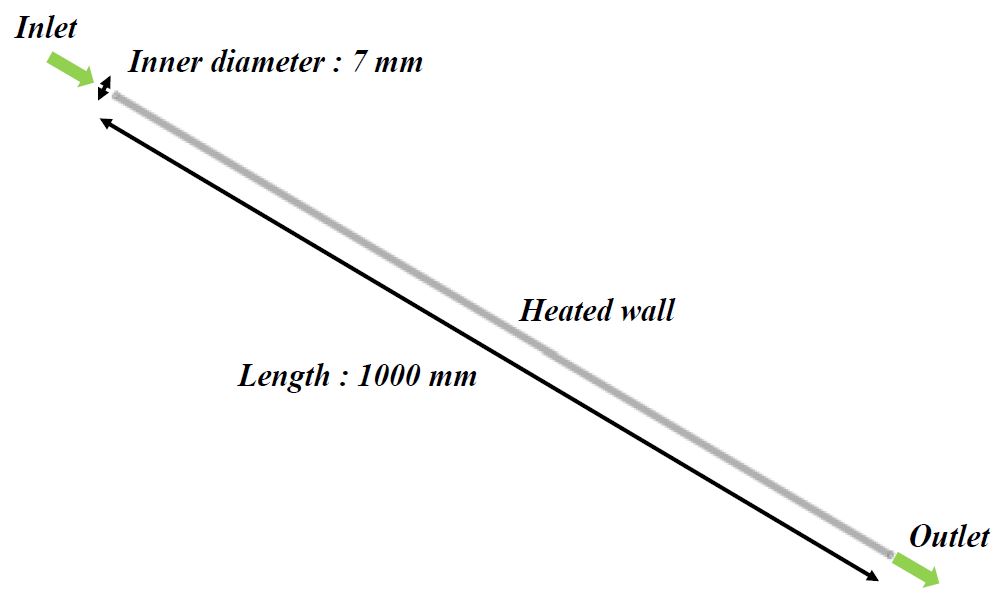
수치해석을 위한 시험부의 형상은 Esmaeilzadeh et al.[8]의 실험에서 사용된 것과 동일하게 Figure 1과 같이 구성되었다. 길이 1m, 내경 7mm의 수평 원관이 사용되었으며, 벽면에는 9000 W/m2의 열유속이 공급된다.
기반 유체로서 물이 사용되었으며, 나노입자는 알루미나(Al2O3)가 사용되었다. Esmaeilzadeh et al. [8]의 실험에 사용된 입자의 직경은 10-20 nm이며, 수치해석에서는 평균 직경인 15nm를 적용하였다. 나노입자의 농도는 체적분율 0.5와 1%에 대해서 수행되었으며, 입구 조건으로 Reynolds number 470-1900에 해당하는 질량유속이 적용되었다. 출구는 1대기압으로 분출되는 것으로 가정하였으며, 이러한 경계조건은 Table 1에 정리하였다.
3. 결과 및 고찰
수치해석은 물과 0.5, 1%의 체적 분율을 가지는 나노유체에 대해서 수행되었으며, Esmaeilzadeh et al. [8]의 실험결과와 비교하였다. 또한 물의 수치해석에서는 Shah[18]의 상관식을 사용하여 수치해석과 실험결과[8]의 유효성을 확인하였다. 국소 열전달 계수 h와 국소 Nusselt number Nu는 다음 식과 같이 계산된다.
| (10) |
| (11) |
여기서 d는 관의 직경을 의미하며, q″ 은 열유속, 그리고 Tw와 Tf는 각각 벽의 온도와 단면의 유체 평균 온도를 의미한다. Tf는 에너지 평형식에 의해서 다음과 같이 계산된다.
| (12) |
여기서 Tin은 입구 온도를 나타내며, P는 접수둘레, x는 입구에서 온도가 측정된 지점까지의 거리, υ는 유체의 평균속도, A는 관의 단면적을 의미한다.
일정한 열유속 조건에서 층류 유동에 관한 Shah[18]의 상관식은 식 (13)과 같이 표현된다.
| (13) |
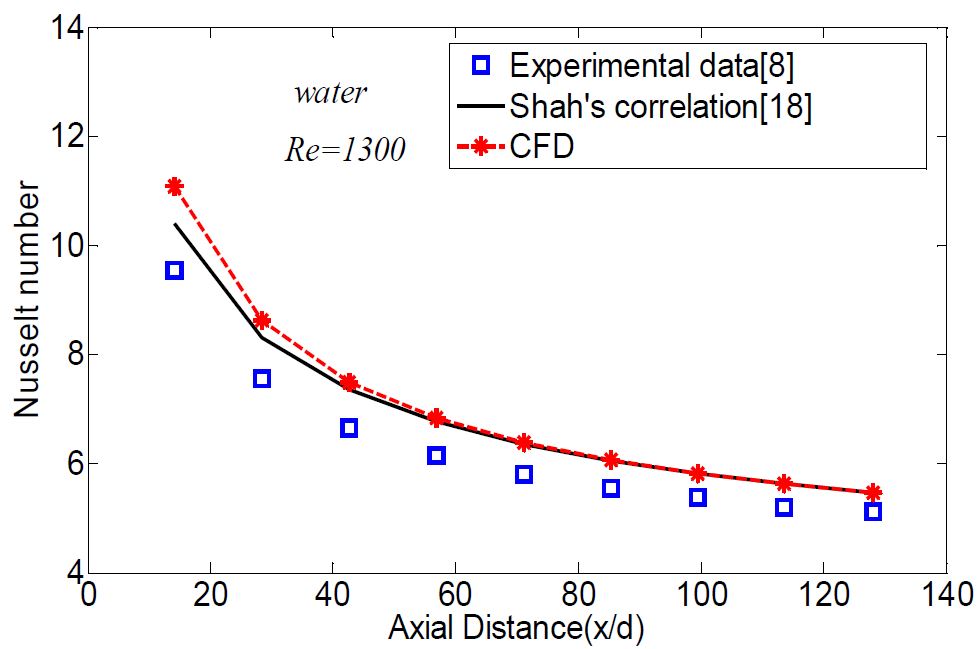
Figure 2는 Reynolds number 1300에서 유동방향의 무차원 거리(x/d)에 따른 Nusselt number를 실험결과[8]와 Shah[18] 상관식에 의한 값 그리고 수치해석에 의한 결과를 나타낸 것이다.
상관식과 수치해석에 의한 예측은 대체적으로 실험결과를 잘 예측하고 있다. 입구영역에서는 높은 Nusselt number가 나타나며 유동방향으로 진행함에 따라서 Nusselt number는 감소하는 것으로 나타난다. 이것은 원관 층류 유동에서 입구 길이에 대한 해석적 풀이에 의해서 얻어진 국소 Nusselt number의 경향[19]과 일치한다.
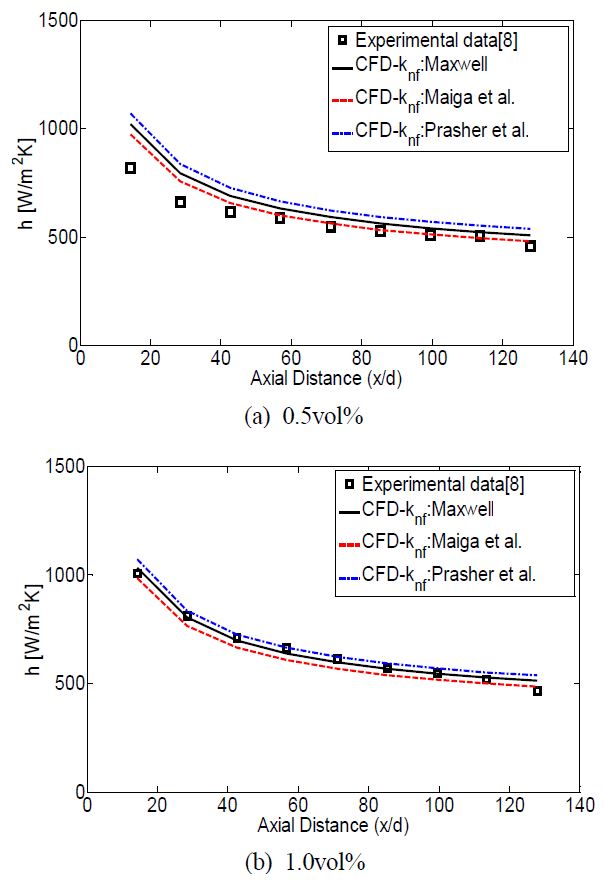
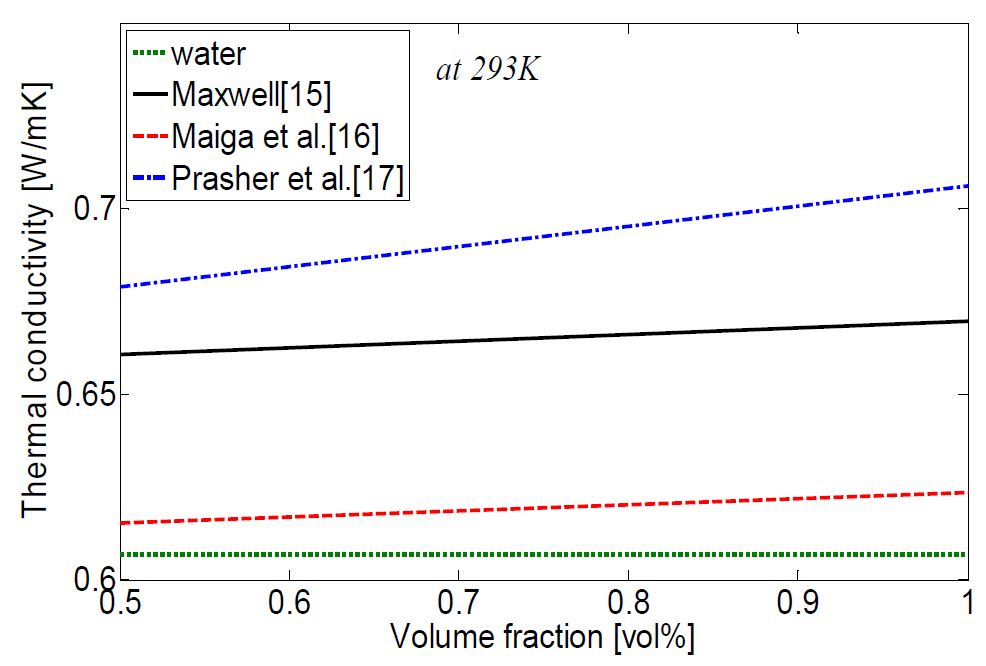
Figure 3 (a)와 Figure 3 (b)는 각각 0.5vol%와 1.0vol% 에서의 유동방향의 무차원 거리에 따른 열전달 계수를 나타낸 것이다. 모든 경우 입구영역과 가까운 지점에서 높은 열전달 계수가 나타났으며, 출구로 갈수록 열전달 계수는 감소하였다. 수치해석에 의한 예측은 전반적으로 실험결과와 잘 일치하였다. 하지만 열전도도 상관식의 적용에 따라서 다소 차이는 발생하였다. Prasher et al. [17]의 상관식을 적용한 경우 가장 높게 열전달 계수를 예측하였으며, Maxwell [15], Maiga et al. [16] 순으로 높게 예측되었다. 이것은 Figure 4에 의해서 설명된다. Figure 4는 293K 에서 체적분율에 따른 각 상관식에 의한 열전도도를 나타낸 것이다. Prasher et al. [17]에 의한 상관식이 열전도도를 가장 높게 예측하는 것을 볼 수 있다.
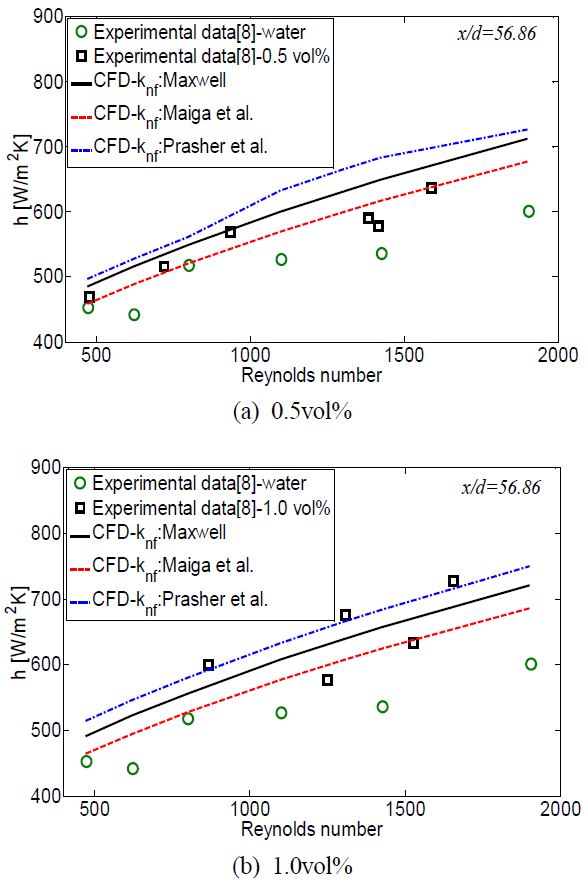
Figure 5는 유동방향 무차원 거리 56.86에서 Reynolds number에 따른 열전달 계수를 나타낸 것이다. 0.5vol%와 1.0vol% 모두 물에 비해서 높은 열전달 계수가 얻어졌으며, 수치해석 결과 또한 물에 비해서 높게 예측하고 있음을 알 수 있다. 이것은 입자의 체적 분율의 증가와 함께 식 (4) ~ 식 (9)에 의해서 계산된 밀도, 비열, 열전도도가 증가하기 때문이다. 다만 나노유체에 대한 실험값은 Reynolds number의 증가에 따라서 일정하게 증가하는 것이 아니라 증가와 감소를 반복하며 증가하는 것으로 나타난다. 이것은 실험 오차에서 기인하는 것으로 불확실성 5-10%를 감안하면[8], 수치해석 결과는 실험결과를 잘 예측하고 있는 것으로 판단된다. 입구영역에서 물과 비교하여 나노유체의 열전달 계수는 0.5vol%에서 최대 11%, 1.0vol%에서 최대 15% 증가하였다.
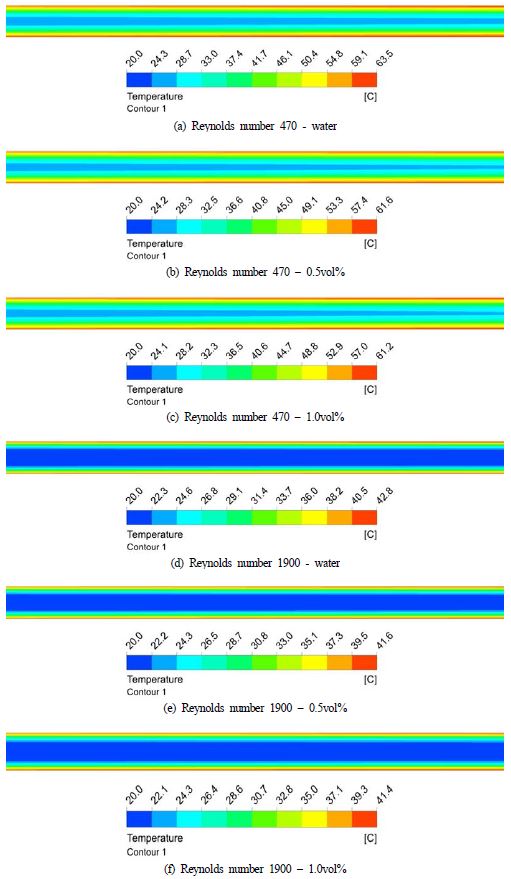
Figure 6은 출구 측에서의 온도분포를 나타낸 것이다. Figure 6 (a) ~ (c)는 각각 Reynolds number 470에서 물과 Maiga et al. [16]의 상관식을 사용한 0.5vol%, 1.0vol%의 결과이며, Figure 6 (d) ~ (f)는 Reynolds number 1900 일 때의 결과이다. Figure 5에서 이미 고찰한 바와 같이 Reynolds number의 증가에 따라서 열전달 계수는 상승하며 그 결과로 출구에서는 낮은 온도가 나타난다. 마찬가지로 물에 비해서 나노 유체를 사용한 경우 출구에서 낮은 온도가 나타났으며, 1.0vol%에서는 0.5vol%에 비해서 다소 낮은 온도가 나타났다.
본 연구에서는 10-20nm의 직경의 입자에 대한 수치해석을 수행하였으며, Reynolds number의 변화와 나노유체의 열전도도 상관식에 따른 열전달 계수의 변화를 분석하였다. Izadi et al. [20]에 따르면 단상 모델 접근법은 100nm 이하의 직경을 가지는 고체 입자에서 좋은 결과를 내는 것으로 보고하였다. 본 연구에서도 단상 모델을 이용한 수치해석 결과는 실험 결과와 잘 일치하는 것을 확인하였다.
4. 결 론
본 연구에서는 단상 모델을 이용한 알루미나/물 나노유체의 열전달 특성에 관한 수치해석적 연구를 수행하였으며, 다음과 같은 결론을 얻었다.
1. 관 입구 측에서 높은 Nusselt number 및 열전달 계수가 나타났으며, 유동 방향으로 진행함에 따라서 Nusselt number 및 열전달 계수는 감소하였다.
2. Reynolds number의 증가에 따라서 열전달 계수는 증가하였으며, 1.0 vol%의 나노유체에서 물과 비교해서 최대 15% 증가하였다.
3. 단상 모델에서의 열전도도를 계산하기 위해서 Maxwell [15], Maiga et al. [16], Prasher et al. [17]의 상관식을 사용하였으며, 상관식에 의해 계산된 열전도도는 Prasher et al., Maxwell, Maiga et al. 순으로 높게 나타났다. 열전도도에 따른 열전달 계수는 다소 차이가 발생하였으나, 실험의 불확실성을 고려하면 세 상관식 모두 실험 결과[8]를 잘 예측할 수 있다고 판단된다.
4. 본 연구의 나노입자 평균 직경인 15nm에서는 단상 모델이 유효하게 적용될 수 있는 것으로 판단되며, 추후 다양한 종류의 나노유체와 다양한 직경의 나노입자에 대해서도 수치해석의 유효성 검토가 요구되며, 또한 단상 모델뿐만 아니라 2상 모델 기법에 대한 폭넓은 연구가 요구된다.
References
- S. U. S. Choi, and J. A. Eastman, “Enhancing thermal conductivity of fluids with nanoparticles, in developments applications of non newtonian flows”, American Society of Mechanical Engineers, 231, p99-106, (1995).
- K. Son, J. S. Lee, T. H. Park, and K. H. Park, “Convective heat characteristics of diamond nanofluid produced by matrix synthetic method”, Journal of the Korean Society of Marine Engineering, 37(1), p9-15, (2013), (in Korean).
-
A. S. Ahuja, “Augmentation of heat transport in laminar flow of polystyrene suspensions. I. experiments and results”, Journal of Applied Physics, 46(8), p33408-3416, (1975).
[https://doi.org/10.1063/1.322107]

-
K. H. Park, J. A. Lee, and H. M. Kim, “Heat conductivity test and conduction mechanism of nanofluid”, Journal of the Korean Society of Marine Engineering, 32(6), p862-868, (2008), (in Korean).
[https://doi.org/10.5916/jkosme.2008.32.6.862]

-
P. Keblinski, S. R. Phillpot, S. U. S. Choi, and J. A. Eastman, “Mechanisms of heat flow in suspensions of nano-sized particles (nanofluids)”, International Journal of Heat and Mass Transfer, 45(4), p855-863, (2002).
[https://doi.org/10.1016/s0017-9310(01)00175-2]

-
D. Wen, G. Lin, S. Vafaei, and K. Zhang, “Review of nanofluids for heat transfer applications”, Particuology, 7, p141-150, (2009).
[https://doi.org/10.1016/j.partic.2009.01.007]

-
D. Wen, and Y. Ding, “Experimental investigation into convective heat transfer of nanofluids at the entrance region under laminar flow conditions”, International Journal of Heat and Mass Transfer, 47(24), p5181-5188, (2004).
[https://doi.org/10.1016/j.ijheatmasstransfer.2004.07.012]

- E. Esmaeilzadeh, H. Almohammadi, Sh. N. Vatan, and A. N. Omrani, “Experimental investigation of hydrodynamics and heat transfer characteristics of γ -Al2O3/water under laminar flow inside a horizontal tube”, International Journal of Thermal Sciences, 53, p31-37, (2013).
- Y. G. Kim, S. H. Jo, Y. J. Seong, H. S. Chung, and H. M. Jeong, “Experimental investigation of heat transfer characteristics of alumina nanofluid”, Journal of the Korean Society of Marine Engineering, 37(1), p16-21, (2013), (in Korean).
-
M. K. Moraveji, M. Darabi, S. M. J. Haddad, and R. Davarnejad, “Modeling of convective heat transfer of a nanofluid in the developing region of tube flow with computational fluid dynamics”, International Communications in Heat and Mass Transfer, 38(9), p1291-1295, (2011).
[https://doi.org/10.1016/j.icheatmasstransfer.2011.06.011]

-
K. B. Anoop, T. Sundararajan, and S. K. Das, “Effect of particle size on the convective heat transfer in nanofluid in the developing region”, International Journal of Heat and Mass Transfer, 52(9-10), p2189-2195, (2009).
[https://doi.org/10.1016/j.ijheatmasstransfer.2007.11.063]

-
I. Behroyan, P. Ganesan, S. He, and S. Sivasankaran, “Tubulent forced convection of Cu-water nanofluid: CFD model comparison”, International Communications in Heat and Mass Transfer, 67, p163-172, (2015).
[https://doi.org/10.1016/j.icheatmasstransfer.2015.07.014]

-
Y. Xuan, and Q. Li, “Investigation on convective heat transfer and flow features of nanofluids”, Journal of Heat Transfer, 125(1), p151-155, (2003).
[https://doi.org/10.1115/1.1532008]

-
A. Einstein, Investigations on the Theory of the Brownian Movement, Courier Corporation, (1956).
[https://doi.org/10.1088/0031-9112/7/10/012]

- J. C. Maxwell, A Treatise on Electricity and Magnetism, London, Oxford University Press, (1904).
- S. E. B. Maiga, S. J. Palm, C. T. Nguyen, G. Roy, and N. Galanis, “Heat transfer enhacement by using nanofluids in forced convection flows”, International Journal of Heat and Fluid Flow, 26(4), p530-546, (2005).
-
R. Prasher, P. Bhattacharya, and P. E. Phelan, “Thermal conductivity of nanoscale colloidal solution (nanofluids)”, Physical Review Letters, 94(2), p025901-1-4, (2005).
[https://doi.org/10.1103/physrevlett.94.025901]

- R. K. Shah, “Thermal entry length solutions for the circular tube and parallel plates”, Proceedings of 3rd National Heat and Mass Transfer Conference, 1, pHMT-11-75, (1975).
- W. M. Kays, and M. E. Crawford, Convective Heat and Mass Transfer, McGraw-Hill, 3rd Ed., (1993).
-
M. Izadi, A. Behzadmehr, and D. Jalali-Vahida, “Numerical study of developing laminar forced convection of a nanofluid in an annulus”, International Journal of Thermal Sciences, 48(11), p2119-2129, (2009).
[https://doi.org/10.1016/j.ijthermalsci.2009.04.003]