해양플랜트용 방화 댐퍼의 내화성능에 관한 수치해석
Copyright ⓒ The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
본 연구에서는 해양플랜트용 방화 댐퍼의 내화성능을 확인하기 위한 수치해석적 연구를 수행하였다. 수치해석을 위해서 상용코드인 ANSYS-CFX 13.0을 이용하였으며, 전도, 자연대류 그리고 복사 열전달을 고려하였다. 수치해석 결과는 방화 댐퍼 내부의 단열 유무에 따른 기존의 실험결과와 비교하였다. 또한 복사 열전달 방정식을 풀기위해서 상용코드에서 제공하는 여러 모델들을 사용하여 각 모델들의 결과를 비교하였다. 여러 복사 모델들 중 P-1 모델이 실험 데이터와 비교하여 가장 유사하게 예측하였으며, discrete transfer 모델과 Monte Carlo 모델은 방화 댐퍼의 내화성능을 잘 나타내지 못하였다. 본 수치해석 결과를 통해서 추후 실험에서 보완되어야 할 사항을 도출하였으며, 해양플랜트용 방화 댐퍼의 설계에 대한 기초 자료를 확보 할 수 있었다.
Abstract
In this paper, we present a numerical analysis to verify the fireproof performance of fire damper for offshore plants. The commercial code ANSYS-CFX 13.0 was used for the numerical analysis pertaining to conduction, natural convection, and radiation heat transfer. Numerical results were compared to experimental results found in the literature. Of the different radiation heat transfer models, the P-1 model agreed satisfactorily with the experimental data, while the Monte Carlo model and discrete transfer model resulted in over-prediction. The parameters required for subsequent experiments were derived from the numerical results; further, preliminary data on fire damper for offshore plants were obtained.
Keywords:
Computational fluid dynamics (CFD), Fire damper, Numerical analysis, Offshore plant, P-1 model, Radiation heat transfer키워드:
전산유체역학, 방화 댐퍼, 수치해석, 해양플랜트, P-1 모델, 복사 열전달1. 서 론
선박이나 해양플랜트의 경우 화재 발생에 대비한 여러 안전 장비들을 필수적으로 구비하여야 하며, 이러한 사항은 해상인명안전협약(SOLAS, International Convection for the Safety of Life at Sea)과 각 선급(Class)의 규정에 따라 규정된다. 여기에는 화재 감지기 및 스프링 쿨러 등의 소화 시스템뿐만 아니라 화재 확산을 방지하기 위한 방화 구획과 덕트 그리고 방화 댐퍼 등이 포함된다[1].
일반 선박에서는 표준화재 등급에 해당하는 A 등급 기자재가 설치되는 반면에 해양플랜트의 경우 가연성 물질을 취급하므로 표준화재 등급에 비해서 높은 기준인 탄화수소화재(hydrocarbon fire)등급에 해당하는 H 등급의 기자재가 설치되어야한다. 하지만 국내 기자재 산업의 기술개발 및 수요는 일반 선박용 A 등급의 기자재에 주로 맞춰져 있으며, H 등급의 기자재는 현재까지 개발 및 설계, 적용이 미흡한 단계이다[2].
해양플랜트에 적용되는 H-120 등급은 120분 동안 최고온도상승이 180℃ 이하로 유지되는 것을 의미하며, Choi et al. [2]은 H-120 등급의 방열성능 확보를 위한 방화 댐퍼의 블레이드 내부의 단열 유무에 따른 실험을 수행하였다. 실험 결과에 따르면 댐퍼 블레이드의 단열 조건이 방화 댐퍼의 내화 성능에 큰 영향을 미치는 것으로 나타났으며, 단열 조건하의 실험 시 H-120 등급의 내화 성능을 확보하였다.
그리고 Choi et al. [1]은 코밍 노출면 단열 두께 및 단열 길이 변화에 따른 내화 성능을 확인하기 위해서 실험적 연구를 수행하였으며, 지정된 조건에서의 최적의 단열 두께 및 단열 길이를 확보하였다.
H 등급 내화 성능을 확인하기 위해서는 대부분 실험에 전적으로 의존하고 있는 실정이며, 최적의 조건을 도출하기 위해서는 다양한 변수를 토대로 많은 실험을 수행하여야 한다. 앞으로 해양플랜트 산업의 발전과 전망을 고려하면 H 등급 기자재의 기초 설계를 위한 기본 자료를 충분히 확보할 필요가 있으며, 이것은 수치해석적 연구로 대체가능 할 것으로 판단된다. 전산유체역학(CFD, Computational Fluid Dynamics)을 이용한 수치해석적 연구는 설계 단계에서 일부 실험을 대체함으로써 개발기간과 비용을 단축시킬 수 있으며, 고온ᐧ고압 등 위험한 조건에서도 시뮬레이션이 가능하며, 측정 지점 마다 장비를 추가해야하는 실험에 비해서 거의 모든 지점에서의 물성값을 확인할 수 있는 등의 여러 장점이 있다[3].
일반적인 열ᐧ유동 해석에서 복사는 고려하지 않는 경우가 많으나, 연소와 같이 고온의 해석 범위나 낮은 온도 범위일지라도 부력에 의한 열 플럭스가 작아서 복사에 의한 열 플럭스를 무시할 수 없는 자연 대류의 경우 복사를 고려해야 한다.
Martyushev and Sheremet[4]는 밀폐된 사각형 공간에서의 일정한 열원을 가지는 계산영역에 대해서 2차원 수치해석을 수행하였다. 그들은 과도 자연대류와 표면 열 복사와 전도를 결합한 열전달 해석을 진행하였으며, Rayleigh number, 표면 방사율(surface emissivity), 표면에서의 고체와 유체의 열전도도의 비 그리고 고체 벽면의 두께와 빈 공간의 길이의 비를 대류와 복사 열전달에 영향을 미치는 중요한 요소로 판단하였다.
Habibi et al. [5]은 증기 분해 가열로에서의 3차원 해석을 수행하였다. 난류 모델로는 RNG k-ε 모델을 사용하였으며, 복사 모델로는 이산 종좌표 모델(DOM, discrete ordinates model), P-1 그리고 Rosseland 모델을 사용하였다. 수치해석 결과에 따르면 DOM과 P-1 모델이 가장 정확하게 예측하였다.
Ergin [6]은 가열된 2층 구조물에서 전도와 자연대류를 포함하는 표면 복사에 대해서 실험과 수치해석적 연구를 수행하였다. 복사 열전달은 Hottel [7]의 모델을 사용하였으며, 이 모델은 물질을 불투명(opaque)하고 회색체(gray surface)로 가정하며, 일정한 입사강도를 가지는 것으로 가정한다. 실험과 수치해석의 조건에 따른 결과에 의하면 표면에서의 열전달은 주로 대류에 의해서 이루어지는 것으로 나타났으며, 벽면에서의 열전달률 의 분포는 열원의 위치에 크게 의존하며, 열전달량은 입력 열원량과 선형적인 관계가 있다고 보고하였다.
Dongan et al. [8]은 다양한 핀 형상을 가지는 수평 평판에서의 정상상태 자연대류와 복사 열전달에 대한 수치해석을 수행하였으며, 각 핀 배열에서의 열전달 계수를 구하여 최적의 핀 형상을 도출하였다. 복사의 영향을 계산하기 위해서 surface-to-surface 모델을 사용하였다. 유동 패턴과 온도 분포를 최적의 핀 형상을 도출하기 위한 중요한 요소로 판단되어졌으며, 도출된 최적의 핀 형상에서는 일반적인 직사각형의 핀 형상에 비해서 열전달 계수가 2배 가까이 증가하였다.
실제 실험의 경우 비용과 시간적 측면에서 많은 제한이 있으므로 다양한 변수에 대한 실험을 모두 진행하기 어렵다. 해양플랜트용 방화 댐퍼의 경우 현재 충분한 설계 자료들이 축적되지 않았으며, 이는 수치해석으로 일부 대처할 수 있을 것으로 판단한다. 따라서 본 연구에서는 해양플랜트용 방화 댐퍼의 내화 성능에 대한 수치적 연구를 수행하였으며, 수치해석에서는 고체에서의 전도, 그리고 외부 대기에서의 자연 대류 그리고 고온으로 가열된 표면에서의 복사 열전달이 고려되었다. 여러 복사 모델들을 적용하여 비교하였으며, 수치해석의 결과를 Choi et al. [2]의 실험결과와 비교하였다. 본 연구를 통해 얻어지는 결과는 추후 실험에서 보완되어야 할 부분을 비롯해서 해양플랜트용 방화댐퍼 설계의 기초자료로 활용하고자 한다.
2. 수치해석
2.1 방화 댐퍼 형상 및 실험 조건
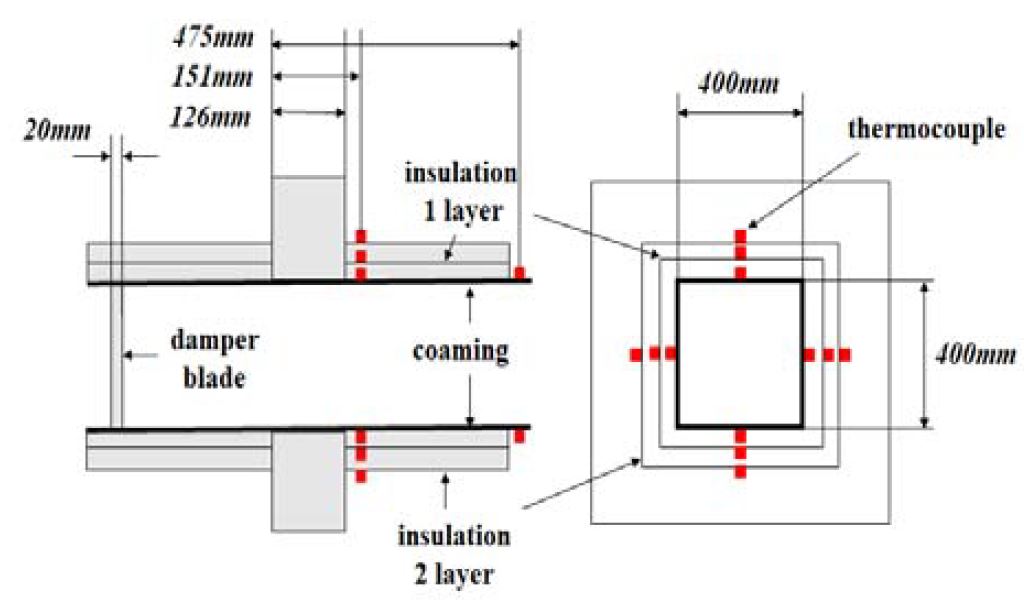
본 연구는 Choi et al. [2]의 실험 조건 및 결과를 토대로 진행되었으며, 실험에 사용된 시험체의 형상은 Figure 1과 같으며, 실험체의 개략도 및 각 부분의 치수는 Figure 2에 나타내었다. 코밍과 블레이드는 SS400 재질로 제작되었으며, 두께는 4.5mm 이다. 단열재는 Morgan Thermal Ceramics 사의 FireMasterⓇ607Ⓡ 제품으로 ceramic wool 재질로 이루어져있다. 실험 case-1과 case-2는 블레이드 내부의 단열 처리 유무에 따라서 구분된다. Figure 2에서 나타낸 바와 같이 코밍 표면과 단열재 표면에 총 16개의 K 타입 표면 열전대에서 측정된 온도를 수치해석에서의 온도와 비교하였다. 실제 실험에서는 Figure 2에서 나타낸 열전대 외에 313mm 지점에 총 4개의 열전대가 추가되었다.
가열로의 내부 온도T 는 식 (1)과 같이 노르웨이 선급 규정의 NDP Fire Temperature Curve에 따라 제어된다.
| (1) |
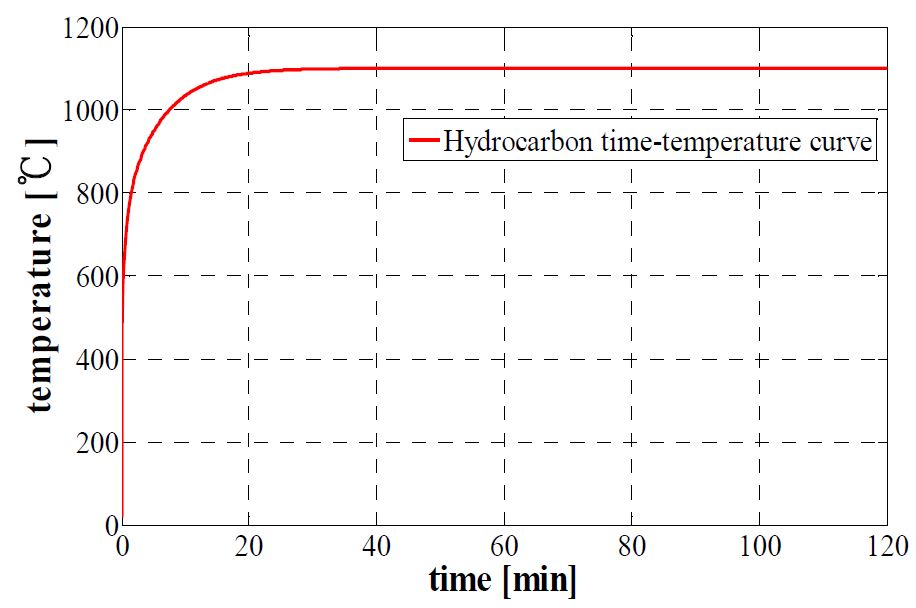
여기서 윗첨자 t는 가열시간(분)을 의미한다. 이 곡선에 의하면 연소가 시작되고 급격하게 온도가 상승하여 약 20분이 경과하면 약 1,100℃의 온도까지 상승하여 이후 거의 일정하게 유지된다. 시간-온도 그래프는 Figure 3과 같다.
2.2 복사 열전달
복사 열전달을 고려하는 문제에서는 에너지 방정식에 복사 열전달 소스항이 추가되며, 이 항은 입사 복사열 플럭스와 방출 복사 열 플럭스를 구해서 정미 복사 열 플럭스를 계산하게 된다. 만약 산란(scattering)이 없는 경우, 복사 열전달 방정식(RTE, radiation transfer equation)은 위치 과 방향 에 대해서 다음과 같이 표현된다[8].
| (2) |
여기서 I 는 복사 강도, a는 흡수율 , n은 굴절률, σ는 Stefan-Bolzmann 상수 그리고 T 는 온도를 나타낸다.
상용코드에서 주로 사용되는 복사 열전달 모델은 Rosseland model, P-1, Monte Carlo model 그리고 discrete transfer 모델 등이 있다[5][9][10].
P-1 모델은 복사 강도를 등방성으로 가정하여 주어진 위치에서 방향에 독립적인 관계를 가지므로, 간단한 형태로 식 (3)과 같이 표현된다.
| (3) |
여기서 qr 은 복사에 의해서 전달되는 열을 의미하며, G는 입사되는 복사열을 의미한다.
P-1 모델이 복사 열 플럭스 벡터를 회색체에서 근사하는 반면에, Rosseland 모델은 표면을 흑체로 취급하며 복사강도를 계산한다. 이 모델은 식 (4)와 같이 표현되며, P-1 모델과 마찬가지로 간단한 형태를 가지므로 계산에 소요되는 시간이 단축되는 장점이 있다.
| (4) |
Monte Carlo 모델은 복사 강도를 광자(photon)의 각 플럭스의 미분에 비례하는 것으로 가정하며, 복사장은 광자 증기로 구성되는 것으로 취급한다. 이 모델은 통계학적인 접근법에 해당하며, 주로 투명한 매체의 복사에서 추천된다.
discrete transfer model은 Monter Carlo 모델과 유사하며, 표면에서의 나오는 광자의 경로, 즉 광선을 추적하여 복사강도를 계산한다. 이 모델은 각 광선의 대역을 분리해서 계산하며, P-1 모델이나 Rosseland 모델에 비해서 계산에 많은 시간이 소모되며, 광학적 두께가 얇은 영역에서는 P-1 모델이나 Rosseland 모델보다 정확하게 예측할 수 있다[9][10].
2.3 해석 조건
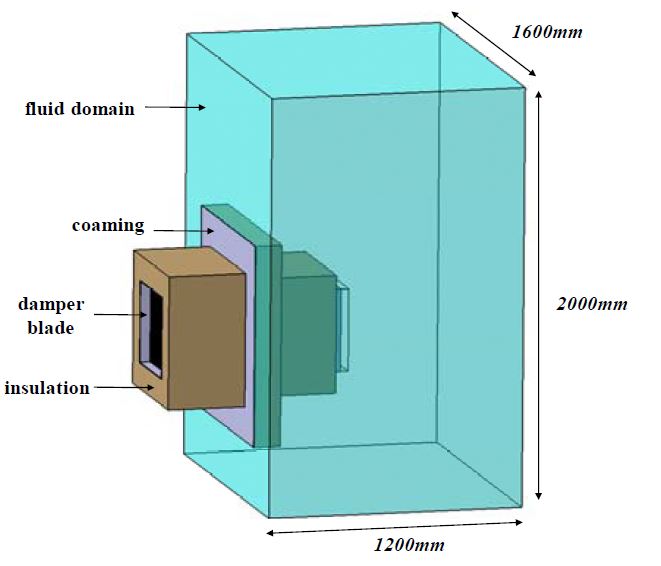
본 연구에서는 Choi et al. [2]의 실험 조건과 동일하게 수치해석을 진행하였으며, 3-D 형상 또한 실험에서 사용한 실험체와 동일한 규격으로 모델링하였으며, Figure 4와 같이 방화 댐퍼 외부에는 유동해석을 위한 유체 계산영역을 생성하였다. 실험 결과에 따르면 연소로 내부의 온도가 시간-온도 그래프와 같이 1,100℃로 유지될 때, 노출면의 온도는 평균적으로 약 1,050℃로 유지되는 것으로 나타났으므로 노출면에서의 온도는 1,050℃로 설정하였으며, 외부 대기의 온도는 실험 조건과 동일하게 13℃로 설정하였다. 외부 압력은 1atm으로 설정하였으며, 방화 댐퍼와 접하지 않는 유체 계산영역의 외부 면에서는 opening 조건을 부여하였다. 작동유체는 공기로서 이상기체로 가정하였다. 낮은 압력에서는 이상기체로 가정하는 것에 큰 오차를 가지지 않는다. 본 수치해석에서는 온도차에 따른 부력에 의해 발생되는 자연대류 현상을 고려하였으며, 자연대류에서는 강제대류의 Reynolds number 대신에 Grashof number를 기준으로 층류와 난류를 구분할 수 있으며, Choi et al. [2]의 실험조건에서는 10 이하의 값을 가지므로 층류 유동으로 가정하였다. 그리고 복사모델은 Rosseland, P-1, discrete transfer, Monte Carlo 모델을 적용하였다. 경계조건을 비롯한 해석조건은 Table 1에 정리하여 나타내었다.
전도 열전달 계산을 위해서 유체 계산영역뿐 아니라 고체 계산영역 영역을 고려해주어야 하는데 고체 계산영역은 코밍, 단열재 그리고 댐퍼 블레이드 이다. 고체에서의 열전달을 계산하기 위한 수치해석에서는 많은 격자를 요구하지 않으므로 고체 계산영역에서는 노드 수 약 27만개의 hexa 격자계가 사용되었으며, 유체 계산영역에서는 온도 구배가 크게 발생하는 영역에서는 조밀한 격자가 요구되어 노드 수 약 88만개의 hexa 격자계가 사용되었다.
본 수치해석에서는 13℃ 외기온도에서 1050℃ 노출면 벽면 온도까지 적용되므로 온도 범위가 큰 편이다. 따라서 온도에 따라서 물성치의 변화를 고려해 주어야 한다. 코밍과 단열재는 각각 SS400과 ceramic wool로 이루어져 있으며, 열전도도 k는 SS400의 경우 Kim and Kang[11]에서 적용한 식을 사용하였으며, ceramic wool의 경우 제조사에서 제공하는 자료를 보간법을 이용하여 구하였다. 본 수치해석에서 사용한 열전도도는 다음과 같다.
| (5) |
| (6) |
3. 결과 및 고찰
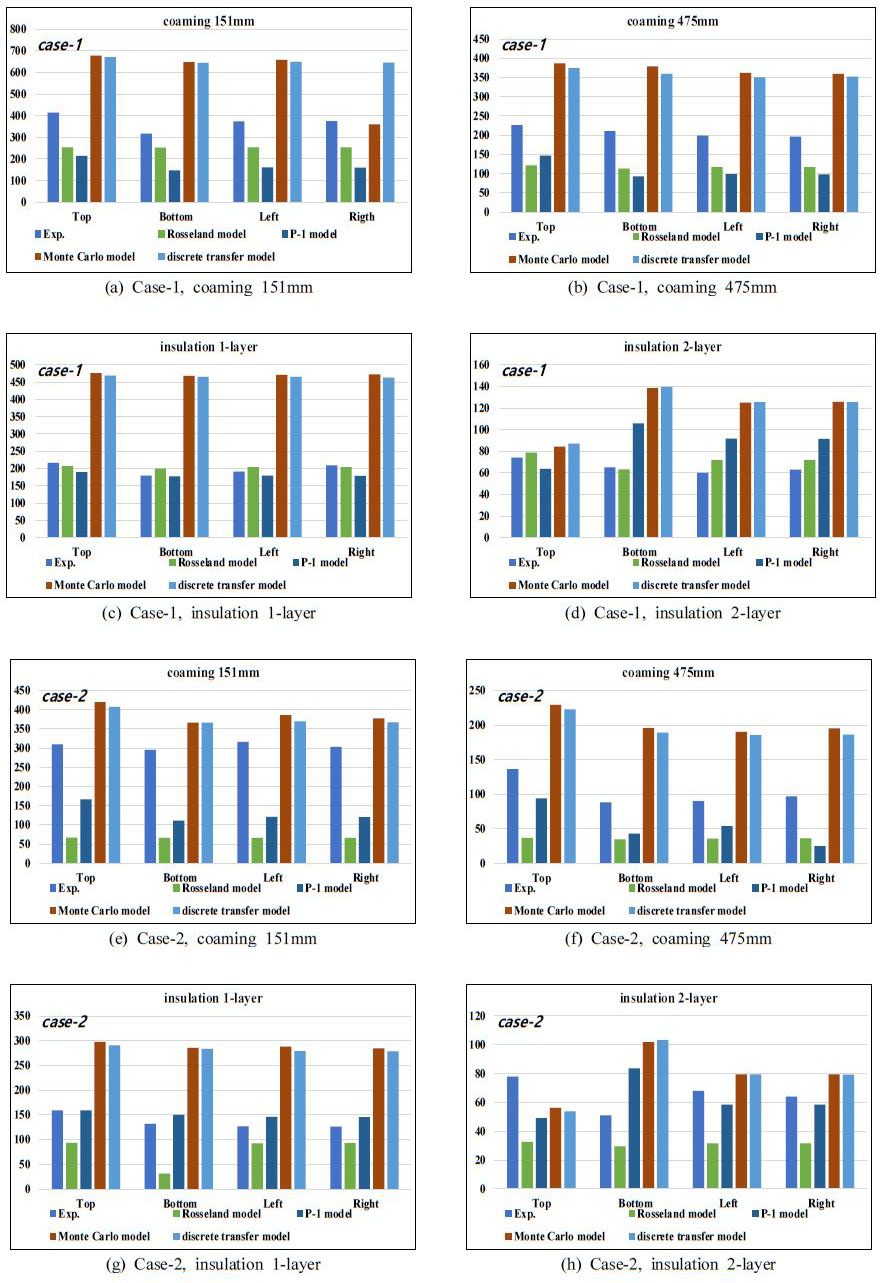
Figure 5는 case-1과 case-2에서 각 열전대 측정 위치에서 실험값과 복사 모델에 따른 수치해석 값을 비교하여 나타낸 것이다. Monte Carlo 모델은 실험값과 비교해서 평균적으로 case-1과 case-2에서 각각 176℃, 87℃ 높게 예측하였으며, discrete transfer 모델은 각각 181℃, 81℃ 높게 예측하였다. 반면에 Rosseland 모델은 각각 49℃, 99℃, P-1 모델은 73℃, 53℃ 낮게 예측하였다. 이때, P-1 모델은 코밍부에서는 온도를 약 110~150℃ 낮게 예측하지만 단열재에서는 case-1 에서는 평균적으로 2.6℃ 높게 예측하였으며, case-2에서는 5.7℃ 높게 예측하였다.
실제 실험에서는 방화 댐퍼가 닫힌 후 연소로에서의 고온의 기체가 댐퍼 블레이드 사이의 틈으로 일부 유출된다. 이 고온의 기체가 직접 전달하는 열은 코밍에서 가장 많이 흡수할 것이고, 이 열은 단열재를 통하는 과정에서 일부 소산되며, 또한 외부의 공기와 혼합되는 과정에서 온도는 급격하게 낮아질 것이다. 수치해석에서는 이처럼 블레이드 틈에서 유출되는 고온의 공기를 고려하지 않았기 때문에 다소 오차가 발생한 것으로 보인다. 유출되는 고온의 공기를 고려하면 코밍에서의 온도는 실험값에 비해서 낮게 나와야 하며, 특히 블레이드와 가까운 지점, 즉 151mm 지점에서의 실험값과 수치해석의 온도차이가 블레이드와 거리가 먼 지점, 즉 475mm에서의 온도차이보다 크게 나타나야 한다고 추측할 수 있다.
그런 측면에서 Rosseland model과 P-1 모델은 실험값에 비해서 온도가 전반적으로 낮게 나오고 있으므로 Monte Carlo 모델이나 discrete transfer 모델에 비해서 실험 조건에 따른 결과를 현실적으로 예측하고 있다고 판단된다.
Rosseland 모델은 case-1의 경우 P-1 모델에 비해서 온도를 평균적으로 약 24℃ 높게 예측하였지만 case-2의 경우 P-1 모델에 비해서 46℃ 낮게 예측하고 있다. P-1 모델은 case-1과 case-2 모두 코밍에서는 실험값에 비해서 낮게 온도를 예측하고 있으나, 단열재에서의 온도는 평균 5.7℃ 이내에서 거의 정확하게 예측하고 있음을 볼 수 있다. 앞서 기술한 블레이드 틈을 통해서 유출되는 고온의 기체를 고려하면 P-1 모델이 가장 현실성 있는 결과를 보여주는 것으로 사료된다.
다만 보다 신뢰성 있는 결과를 확보하기 위해서는 추후 실험에서는 블레이드 틈을 통해서 유출되는 기체의 유량, 온도, 속도 등의 값을 확인할 필요가 있다고 판단된다. 또한 해양플랜트용 방화 댐퍼 개발에서 댐퍼 블레이드 기밀성능이 설계에 중요한 요소임을 확인 할 수 있다.
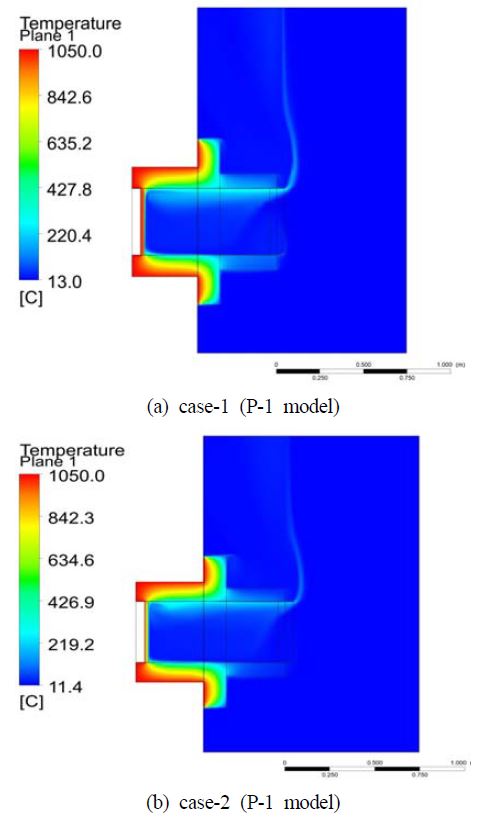
Figure 6 (a)와 Figure 6 (b)는 각각 P-1 모델에서 case-1과 case-2의 온도 분포를 나타낸 것이다. 노출면에서 1,050℃의 벽면 온도는 외부로 접하는 방향으로 진행하면서 급격하게 감소하는 것을 볼 수 있으며, 특히 case-1에 비해서 case-2는 블레이드 댐퍼에서의 온도는 낮게 유지되고 있다. 또한 case-1에서는 case-2에 비해서 비 노출면 단열재의 온도가 더 높게 유지되고 있음을 알 수 있다. 블레이드의 단열 처리가 방화 댐퍼의 내화 성능을 향상시키며, 이것은 실험에서 얻어진 결과와 동일하다.
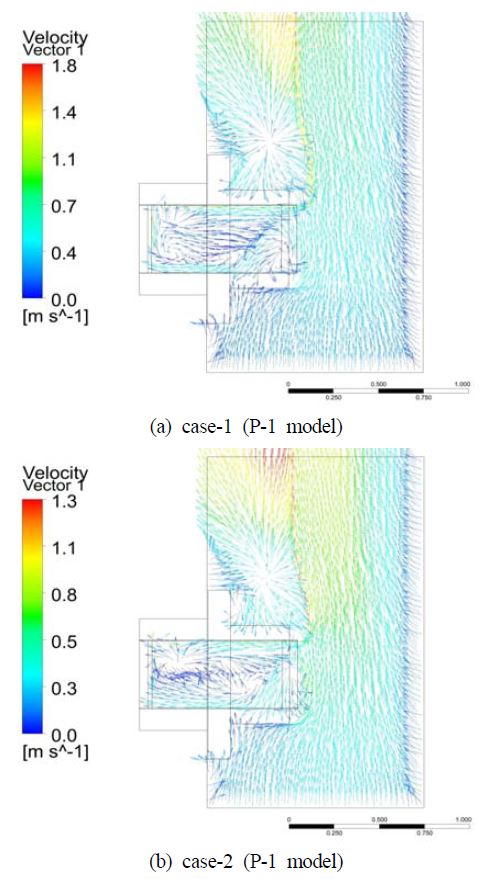
Figure 7 (a)와 Figure 7 (b)는 각각 P-1 모델에서 case-1과 case-2에서의 속도 분포를 나타낸 것이다. 비 노출면에서 상대적으로 높은 온도를 가지는 case-1에서는 최고속도 1.8m/s 로서 case-2의 최고속도 1.3 m/s에 비해서 높게 나타났다. 높은 표면 온도로 인해서 공기가 가열되어, 밀도가 감소하며, 이러한 밀도 차에 의한 부력이 발생한다. 그리고 부력에 의한 자연대류 현상이 이루어지고 있음을 확인 할 수 있다.
4. 결 론
본 연구에서는 기존의 실험 자료를 바탕으로 H-120 등급의 해양 플랜트용 방화 댐퍼의 내화성능에 관한 수치해석적 연구를 수행하였으며, 다음과 같은 결론을 얻었다
- (1) 실험에서는 블레이드의 틈을 통해서 유출되는 고온의 기체로 인해서 코밍의 온도가 높게 측정되었으며, 그러한 현상을 고려하지 않은 본 수치해석 결과는 실험과 다소 차이가 발생하였다. 이러한 현상을 고려하여 분석한 결과 P-1 모델이 가장 현실성 있는 결과를 예측하였다고 판단된다.
- (2) 추후 실험에서는 블레이드 틈을 통해서 유출되는 기체의 유량, 온도, 속도 등의 측정이 필요할 것으로 사료되며, 또한 이것으로부터 블레이드의 기밀 성능이 내화성능에 영향을 미치는 중요한 요소임을 확인하였다.
- (3) 블레이드 내부에 단열처리를 하지 않은 경우(case-1)에 코밍과 단열재가 전체적으로 높은 온도로 유지되었으며, 이로 인해서 자연 대류가 비교적 활발하게 일어난다.
References
-
T. J. Choi, J. S. Kim, Y. S. Lim, K. H. Lee, H. K. Kang, S. H. Park, and Y. T. Kim, “An experimental study on the fireproof performance of fire damper according to change of the insulation conditions on the exposed side and unexposed side of the coaming”, Journal of the Korean Society of Marine Engineering, 38(1), p99-104, (2014), (in Korean).
[https://doi.org/10.5916/jkosme.2014.38.1.99]

-
T. J. Choi, J. S. Kim, K. K. Kim, Y. S. Lim, and Y. T. Kim, “An experimental study on the fireproof performance of fire damper in accordance with insulation conditions on the coaming and blade”, Journal of the Korean Society of Marine Engineering, 37(4), p431-437, (2013), (in Korean).
[https://doi.org/10.5916/jkosme.2013.37.4.431]

- H. K. Versteege, and W. Malalasekera, An Introduction to Computational Fluid Dynamics, 2nd ed., Pearson Education Limited, (2007).
-
S. G. Martyushev, and M. A. Sheremet, “Conjugate natural convection combined with surface thermal radation in an air filled cavity with internal heat source”, International Journal of Thermal Sciences, 76, p51-67, (2014).
[https://doi.org/10.1016/j.ijthermalsci.2013.08.012]

-
A. Habibi, B. Merci, and G. J. Heynderickx, “Impact of radiation models in CFD simulations of steam cracking furnaces”, Computers and Chemical Engineering, 31, p1389-1406, (2007).
[https://doi.org/10.1016/j.compchemeng.2006.11.009]

-
S. Ergin, “Surface radiation with conduction and natural convection in a two-floor enclosure”, 32, p57-70, (2000).
[https://doi.org/10.1016/s0378-7788(99)00034-1]

- H. C. Hottel, Heat Transmission, 3rd ed., McGrawHill, (1954).
- M. F. Modest, Radiative Heat Transfer, 2nd ed, ACAMEMIC PRESS, (2003).
- ANSYS Inc., ANSYS CFX-Solver Theory Guide 13.0, (2010).
- ANSYS Inc., ANSYS CFX-Solver Modeling Guide 13.0, (2010).
-
H. S. Kim, and J. Kang, “Fire resistance performance of concrete filled square steel tube columns with fire spray protection”, Korean Society of Hazard Mitigation, 11(6), p31-37, (2011), (in Korean).
[https://doi.org/10.9798/kosham.2011.11.6.031]