수치해석을 이용한 디젤엔진 연료분사펌프의 캐비테이션 저감에 관한 연구

2.1 CFD 모델링

수치해석 대상은 국내 P사의 L28/32H 중속 디젤엔진용 연료분사펌프[7]이며, CFD 모델링은 연료분사펌프, 고압관 및 연료분사밸브를 대상으로 ANSYS FLUENT R15.0을 사용하여 수치해석 하였다[8]. 연료분사펌프의 구성 부품 중 연료 송출에 직접적으로 영향을 미치는 하우징(housing), 플런저, 바렐 그리고 커넥팅 피스(connecting piece) 등에 대하여 실제 연료분사펌프와 동일하게 모델링하였다. 이 중 플런저는 바렐 내부에서 왕복 운동하며 연료를 송출시키는 역할을 하며, 이를 동적 격자 및 사용자 정의 함수를 적용하여 구현하였다. 또한, 연료분사밸브와 딜리버리 밸브의 모델링은 형상을 단순화하여 동적 격자 및 사용자 정의 함수를 적용하여 개폐 움직임을 적용하였다. 그 이유는 실제형상으로 동적 격자를 적용하여 모델링 한다면 계산 속도 및 재원에 큰 부하를 주는 격자 재생성(remeshing) 기법을 사용하여야하기 때문이다. 형상은 단순화 하였지만 개폐 움직임은 동일하게 적용하였기 때문에 플런저와 바렐의 캐비테이션을 관찰하는데 큰 영향을 미치지 않는다고 판단된다. 격자는 여러 부분으로 나눠 각 부분의 활용에 맞춰 육면체와 사면체 격자로 나눠 생성하였으며, 노드 수는 696만 개이다. 동적 격자가 적용된 부분은 시간 단계를 고려하여 격자의존성을 초과하여 생성하였다[6].

2.2 CFD 해석 조건

CFD 해석 조건은 실험 조건과 동일하며 Table 1에 나타내었다[6]. 컨트롤 랙(control rack) 위치 21 mm는 50% 부하 상태이며[7], 캐비테이션에 영향을 주는 여러 요인 중 유입압력에 따른 캐비테이션을 살펴보기 위해 변수를 유입 압력 3.5 bar, 5.5 bar 및 7.5 bar 세 가지 조건으로 해석하였다.

Table 1:

Conditions of parameter on Experiment and CFD analysis

주 관찰 부분은 캐비테이션에 의해 가장 많이 손상 되는 부분으로 바렐의 내부와 플런저의 리드 부분이다[1].

캐비테이션을 수치해석하기 위한 CFD 해석의 설정을 Table 2에 나타냈다[6]. 난류 모델은 사면체 격자에서 높은 정확성을 얻기 위해 표준 k-ε을 사용하였고, 비정상상태로 해석하였다[9][10].

Table 2:

Setup conditions on CFD analysis

수치해석에 적용된 지배방정식인 일반형 수송방정식은 식 (1)과 같다[11].

여기서, ρ는 유체 밀도, ϕ는 종속변수, Γ는 확산계수 그리고 S 는 생성항이며, 일반형 수송방정식은 비정상항, 대류항, 확산항, 그리고 생성항으로 구성되어있다.

또한, 플런저, 연료분사밸브 및 딜리버리 밸브의 움직임에 적용된 동적 격자의 보존 방정식은 식 (2)와 같다[12].

여기서, V 는 임의의 검사체적, ∂V 는 검사체적의 경계, $$ \overrightarrow{u}$$는 유속 벡터, $$ {\overrightarrow{u}}_g$$는 동적 격자의 격자 속도, $$ \overrightarrow{A}$$는 공간벡터, Γ는 확산계수 그리고 S _ϕ는 ϕ의 생성항이다.

다상혼합유체로 캐비테이션 모델은 Schnerr-Sauer 모델을 사용하였다. Schnerr-Sauer 모델은 증기의 물성 및 증기 기포의 크기와 관련된 계수가 같아 기화 압력에 대한 상대 압력에 따라 기화 및 응축하는 상변화를 모델링 할 수 있기 때문이다. 캐비테이션 해석을 위한 증기 수송방정식은 식 (3)과 같다[13]-[15].

여기서, α 는 증기부피율, ρ_v는 증기밀도 그리고 $$ \overrightarrow{V}$$_v는 증기상 속도 이며, 우변의 R_e - R_c은 기화 압력에 대한 상대 압력에 따라 기화 및 응축하는 상변화를 모델링한 소스항이다. 증기기포 크기는 증기의 체적분율로 계산되므로 식 (3)의 증기 수송방정식으로부터 구하며 기포 반지름 ℜ_B 는 식 (4)와 같다.

증기 압력(vapor pressure)은 해석 조건에 적용된 디젤 55°C의 증기 압력인 0.0133 bar로 설정하였다[16][17].

3.1 유입 압력의 증가에 따른 송출 압력

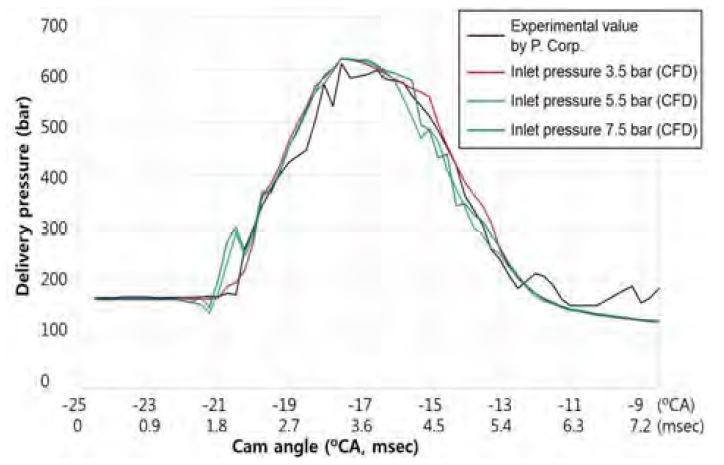
유입 압력의 증가가 연료 송출 압력에 미치는 영향을 고찰하기 위해 유입 압력을 3.5 bar, 5.5 bar, 7.5 bar 세 가지로 수치해석 한 CFD 결과와 실험 결과의 연료 송출 압력을 Figure 1에 비교해보았다. 가로축은 연료 캠 각도(fuel cam angle, °CA)를 나타내며 시간으로 볼 수 있다. 세로축은 연료분사펌프 출구의 연료 송출 압력이다[7].

Figure 1:

Delivery pressure of experimental value and CFD results (inlet pressure 3.5, 5.5, 7.5 bar)

CFD 해석 결과에서 유입 압력이 변하여도 연료 송출 압력의 상승 시작 시점 및 최대 송출 압력이 나타난 시점은 동일하였으며, 실험 결과와 CFD 해석 결과의 최대 송출 압력을 Table 3에 나타내었다.

Table 3:

Maximum delivery pressure of experimental value and CFD results

CFD 해석 결과에서 최대 송출 압력은 유입 압력이 3.5 bar 경우에 비해 5.5 bar, 7.5 bar일 때 각각 0.14%, 0.24% 상승하였다. 연료분사펌프의 유입 압력이 상승하여도 최대 송출 압력에는 큰 영향을 미치지 못했다. 연료 송출 압력의 상승은 플런저의 상승이 주 역할을 하여 송출하기 때문에 바렐 내부로 들어오는 연료의 압력은 큰 영향을 주지 못하였기 때문이다. 하지만 연료분사펌프 유입 관에 누설 발생사고 가능성, 내구성 등의 여러 문제를 고려해야하므로 실제 유입 압력을 상승시켜 운전한다면 추후 보완점이 필요하다고 생각한다.

3.2 유입 압력의 증가가 캐비테이션에 미치는 영향

증기 부피율은 캐비테이션에 의한 손상의 원인이 되는 기화의 부피율을 나타낸 것으로 이는 캐비테이션의 지표가 될 수 있다[13][18]. 증기 부피율이 존재하면 캐비테이션이 발생 또는 발생 가능성이 있다고 판단할 수 있다[15][17].

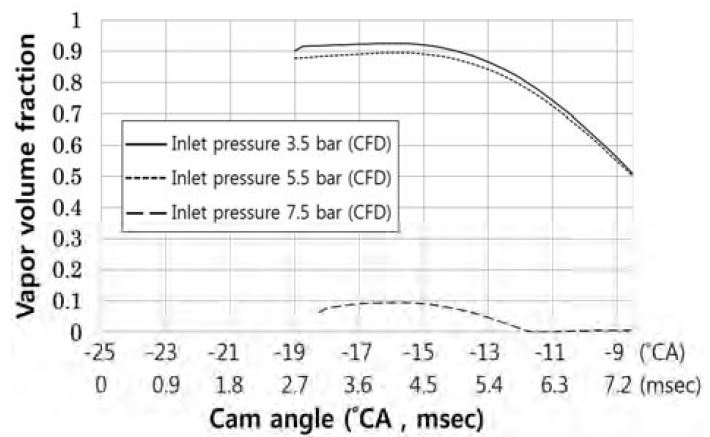
연료분사펌프의 구성 부품 중 캐비테이션에 의해 주로 손상되는 플런저의 리드와 바렐의 스필 포트 부분을 관찰하여보았다[1]-[4]. CFD 해석 결과 중 이 부분의 연료 캠 각도에 따른 평균 증기 부피율을 Figure 2에 나타냈다. 가로축은 연료 캠의 각도이며, 세로축은 이 위치에서의 증기 부피율의 평균값이다.

Figure 2:

Vapor volume fraction of CFD results

캐비테이션이 나타나기 시작한 시점은 유입 압력 3.5 bar와 5.5 bar의 경우 –19.00 °CA에서 나타났으며, 플런저가 바렐의 스필 포트를 막아 연료 송출이 되고 있는 시점이다. 유입 압력 7.5 bar의 경우 0.50 °CA 이후 시점인 –18.50 °CA에서 캐비테이션이 나타났다. 유입 압력 3.5 bar, 5.5 bar, 7.5 bar 경우 모두 캐비테이션이 가장 많이 발생한 시점은 –16.50 °CA이며, 플런저의 리드가 바렐의 스필 포트와 만난 후 시점이다.

Figure 3은 캐비테이션에 의해 손상된 플런저와 CFD 해석 결과에서 캐비테이션이 가장 많이 발생 한 연료 캠 각도 –16.50 °CA일 때를 비교하여 나타낸 것이다. 손상된 플런저는 디젤 엔진에 장착되어 1,000시간 이상 운전 후 분해한 것이다[7]. CFD 해석 결과에서 캐비테이션은 유입 압력 3.5 bar, 5.5 bar의 경우 플런저의 리드 부분에 전체적으로 나타났고 유입 압력 7.5 bar의 경우 플런저의 상부에 집중적으로 나타났다. 특히, 유입 압력 3.5 bar, 5.5 bar의 경우 바렐의 스필 포트에서 캐비테이션이 많이 발생하였다. 이 위치는 플런저와 만나는 위치이며 플런저가 손상된 위치와 유사하다. 그러므로 스필 포트에서 발생하는 캐비테이션이 플런저에 손상을 입힐 것이라 판단된다.

Figure 3:

Damaged plunger and vapor volume fraction contour

최대 송출 압력이 나타난 시점인 연료 캠 각도 –17.50 °CA와 캐비테이션이 가장 많이 발생한 시점인 연료 캠 각도 –16.50 °CA에서 유입 압력에 따른 증기 부피율의 분포를 고찰해보았다.

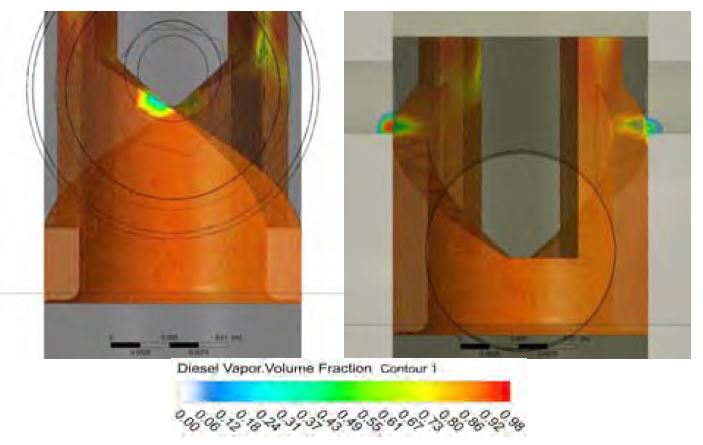
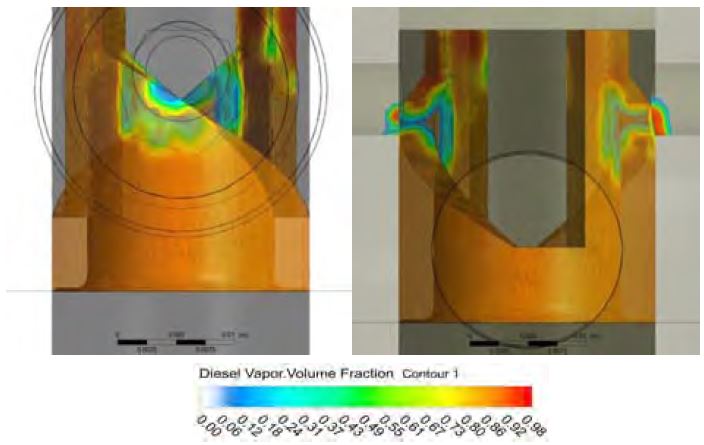
Figure 4는 유입 압력 3.5 bar이며 최대 송출 압력 시점인 연료 캠 각도 –17.50 °CA일 때 증기 부피율의 분포를 나타낸 것이다. 리드와 스필 포트가 만난 시점이며 리드에서 증기 부피율 평균값은 0.9211이다. 리드와 스필 포트가 만나는 부분의 증기 부피율은 0.80 이하로 평균값보다 낮게 나타났지만 스필포트에서는 증기 부피율이 0.90 이상 높은 부분이 나타났다.

Figure 4:

Vapor volume fraction contour for front and side of inlet pressure 3.5 bar at –17.50 °CA

Figure 5는 유입 압력 3.5 bar이며 캐비테이션이 가장 많이 발생한 연료 캠 각도 –16.50 °CA일 때 증기 부피율의 분포를 나타낸 것이다. 증기 부피율의 평균값은 리드에서 0.9257이며, 최대값은 스필 포트에서 0.9882로 나타났다. 스필 포트에서 증기 부피율이 0.10 이상 나타난 부피는 16.05 ㎣ 으로 최대 송출 압력이 나타난 시점보다 확대되었다. 이는 리드와 스필 포트가 만나는 부분이 확대되었기 때문이라 생각한다. 스필 포트에서 증기 부피율이 0.90 이상 높은 부분이 나타났고 이 부분에서 나타난 캐비테이션이 플런저와 만나 손상을 일으킬 것이라 생각된다.

Figure 5:

Vapor volume fraction contour for front and side of inlet pressure 3.5 bar at –16.50 °CA

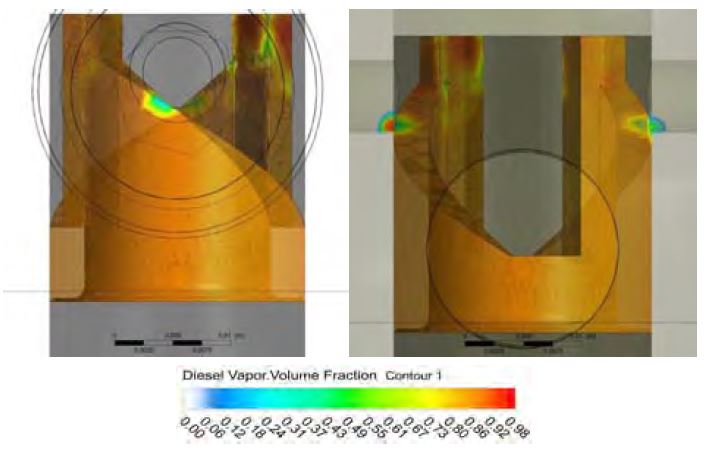
Figure 6은 유입 압력 5.5 bar이며 최대 송출 압력 시점인 연료 캠 각도 –17.50 °CA일 때 증기 부피율의 분포를 나타낸 것이다. 리드에서 증기 부피율 평균값은 0.8880으로 유입 압력 3.5 bar 경우에 비해 3.59% 감소하였다. 스필 포트에서 증기 부피율이 0.90 이상 높은 부분이 발생하였고 이 부분에서 증기 부피율의 평균값은 유입 압력 3.5 bar 경우에 비해 4.04% 감소하였다. 유입 압력 3.5 bar의 경우에 비해 증기 부피율은 감소하였으나 증기 부피율 0.90 이상의 많은 캐비테이션이 발생하고 있으므로 유입 압력 3.5 bar 경우와 마찬가지로 플런저와 스필 포트가 만나는 부분에 큰 손상을 줄 것이라 생각된다.

Figure 6:

Vapor volume fraction contour for front and side of inlet pressure 5.5 bar at –17.50 °CA

Figure 7은 유입 압력 5.5 bar이며 캐비테이션이 가장 많이 발생한 연료 캠 각도 –16.50 °CA일 때 증기 부피율의 분포를 나타낸 것이다. 증기 부피율의 리드에서 평균값은 0.8958으로 유입 압력 3.5 bar 경우보다 3.23% 감소하였으며, 최대값은 스필 포트에서 0.9838으로 나타났다. 스필 포트에서 증기 부피율의 평균값은 유입 압력 3.5 bar 경우에 비해 0.28% 감소하였고 유입 압력 3.5 bar 경우와 마찬가지로 증기 부피율이 0.90 이상 높은 부분이 발생하여 캐비테이션에 의한 손상이 발생한다고 생각된다.

Figure 7:

Vapor volume fraction contour for front and side of inlet pressure 5.5 bar at –16.50 °CA

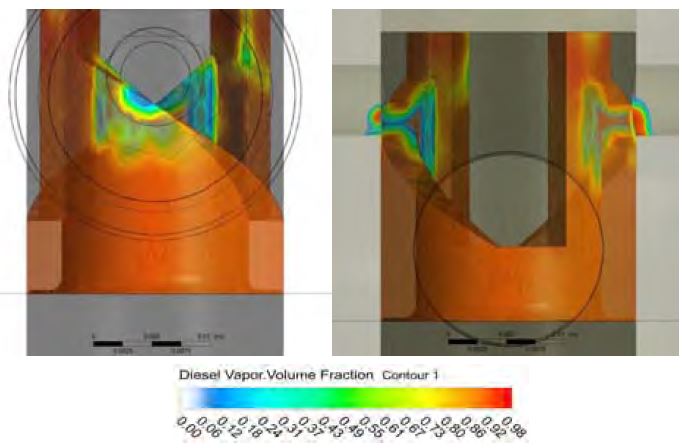
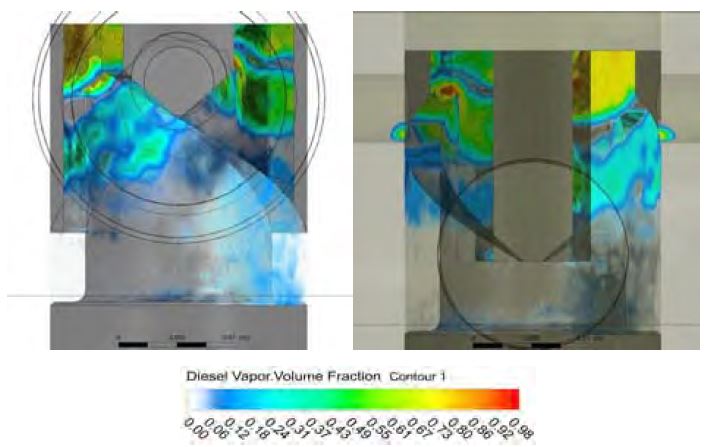
Figure 8는 유입 압력 7.5 bar이며 최대 송출 압력 시점인 연료 캠 각도 –17.50 °CA일 때 증기 부피율의 분포를 나타낸 것이다. 플런저의 리드 부분의 증기 부피율 평균값은 0.0845으로 유입 압력 3.5 bar, 5.5 bar의 경우 보다 90.82%, 90.48% 감소하였다. 스필 포트에서 증기 부피율이 0.80 이상인 부분이 발생하였지만 유입 압력 3.5 bar 경우와 비교하였을 때 증기 부피율 평균값이 46.07% 감소하였다.

Figure 8:

Vapor volume fraction contour for front and side of inlet pressure 7.5 bar at –17.50 °CA

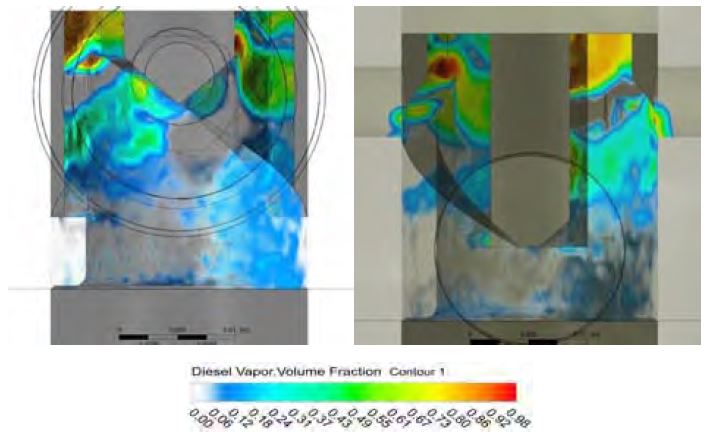
Figure 9는 유입 압력 7.5 bar이며 캐비테이션이 가장 많이 발생한 연료 캠 각도 –16.50 °CA일 때 증기 부피율의 분포를 나타낸 것이다. 리드의 증기 부피율 평균값은 0.0946으로 유입 압력 3.5 bar 경우보다 89.78% 감소하였다. 증기 부피율의 평균값이 89.78% 감소한 것에 비해 최대값은 0.96% 감소하였는데, 이는 플런저의 수직 홈의 극소 부분에서만 나타났으며 전체적인 캐비테이션은 감소하였다. 플런저의 수직 홈 지점에서 증기 부피율의 최대값이 나타난 것은 이 지점이 연료 송출 과정에 의해 가압된 바렐 내부와 맞닿아 차압이 크게 발생하는 지점이기 때문이라 생각한다. 스필 포트에서 증기 부피율의 평균값은 유입 압력 3.5 bar 경우에 비해 40.78% 감소하였으며 캐비테이션이 발생한 부피 또한 17.88% 감소하여 플런저에 주 손상을 입히는 위치의 캐비테이션이 감소하였다고 생각한다.

Figure 9:

Vapor volume fraction contour for front and side of inlet pressure 7.5 bar at –16.50 °CA

캐비테이션이 가장 많이 발생 한 연료 캠 각도 –16.50 °CA일 때 플런저의 리드와 바렐의 스필 포트에서 발생한 증기 부피율을 종합하여 Table 4에 나타내었다.

Table 4:

Vapor volume fraction at –16.50 °CA lead of plunger and spill port of barrel

플런저의 리드에서 증기 부피율은 3.5 bar, 5.5 bar, 7.5 bar 세 가지 유입 압력 조건 모두 최소값이 평균값 및 최대값에 비해 미소량으로 나타났다. 증기 부피율의 평균값은 유입 압력 7.5 bar 의 경우, 3.5 bar 에 비해 89.78% 감소하여 확연하게 캐비테이션이 저감되었다고 판단된다. 저감된 이유는 유입 압력의 상승으로 연료 송출 과정에서 바렐 내부의 차압이 줄어들었기 때문이라 생각되며, 추후 캐비테이션이 저감되는 유입 압력의 기준 및 7.5 bar 이상으로 유입 압력을 상승시켰을 경우에 관한 연구가 진행되어야 한다고 생각한다. 증기 부피율의 최대값은 유입 압력이 높을 수록 평균값이 줄어든 것에 비해 크게 줄어들지 않았다. 하지만 유입 압력 7.5 bar의 경우 증기 부피율의 최대값은 플런저의 수직 홈의 극소 지점에서만 나타났다. 이 부분은 연료 송출 과정에 의해 가압된 바렐 내부와 맞닿아 차압이 크게 발생하는 부분이며, 플런저가 캐비테이션에 의해 손상되는 스필 포트와 만나는 부분과는 다른 부분이다. 그러므로 증기 부피율의 최대값은 캐비테이션에 의한 손상을 판단하는데 기준이 되지 않는다고 생각한다.

바렐의 스필 포트에서 증기 부피율의 평균값은 유입 압력 3.5 bar 경우보다 5.5 bar, 7.5 bar 상승시켰을 때 0.28%, 40.78% 감소하였다. 증기 부피율이 0.10 이상 나타난 부피는 유입 압력 3.5 bar 경우보다 5.5 bar, 7.5 bar 상승시켰을 때 3.74%, 17.88% 감소하였다.

유입 압력을 5.5 bar 까지 상승 시켰을 경우 캐비테이션이 많이 저감되지 않았고, 7.5 bar까지 상승시켰을 때 캐비테이션 저감 효과가 크다고 판단된다.