유체 격자 시스템에 따른 유체-구조 연성 결과 분석 및 검증
Copyright ⓒ The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
본 논문은 격자 시스템의 차이에 따라서 구조-유체 연성(fluid-structure interaction, FSI) 해석에 미치는 영향을 분석하였다. 대상물은 FSI해석에서 대표적으로 사용하는 수치적 벤치마크 모델을 사용하였다. 이 모델은 실린더와 실린더 후면에 탄성을 가진 판으로 구성되어 있다. 그리고 이 물체는 비압축성 층류 채널유동에서 거동한다. 탄성을 가진 판은 실린더 주위에서 생성된 와류에 의하여 주기적으로 변형한다. 유체 도메인에서 유동을 해석하기 위한 격자는 벽주위에 잘 분포시켜야 하고, 변형될 격자는 해석결과에 영향을 미치면 안 된다. 따라서 본 연구에는 두 가지의 격자 시스템을 이용하여 해석 결과에 미치는 영향을 살펴보았다. 첫 번째 방법은 대상물의 변형을 모핑(morphing) 기법을 사용하여 구현하고, 두 번째 방법은 중첩격자(overset mesh) 기법과 모핑 기법을 함께 사용한 방법이다. 해석은 구조와 유체에 대한 각각의 상용프로그램을 사용하였고 쌍방 연성(two-way coupling) 방법을 사용하여 연성하였다. 격자 시스템의 차이에 따른 변형 및 힘의 특성에 대하여 비교하였으며, 수렴성에 차이가 있는 것을 확인하였다.
Abstract
This paper shows the effect on fluid-structure interaction (FSI) analysis according to the deformation method of the grid system in a fluid domain. The object is a numerical benchmark model commonly used for FSI analysis composed of a cylinder and an elastic tail in incompressible laminar channel flow. The elastic tail plate is periodically deformed due to the vortices around the cylinder. The grids in the fluid domain should be well distributed around the object in order to analyze flow successfully, thus the deformation of the grids around the object should not affect the quality of analysis result. Two grid systems are applied for the fluid domain in this research. One is to deform the total grid using a morphing method. The other is to deform the partial grid using both an overset gird method and a morphing method. Two commercial codes for the fluid and structure solvers are applied for the analyses with two-way coupling. The deformation characteristics of the elastic tail plate are compared with two grid systems, showing the difference in the convergency of solution.
Keywords:
Fluid-structure interaction (FSI), Two-way coupling, Morphing method, Overset grid키워드:
구조-유체 연성(FSI), 쌍방 연성, 모핑 기법, 중첩격자1. 서 론
유체-구조 연성(Fluid-Structure Interaction, FSI)은 유체역학과 구조역학이 결합되어 있는 복합적인 현상을 해석하는 분야이다. 이 두 가지 역학은 서로 독립적으로 발전해왔으며, FSI 해석을 위하여 독립적인 두 역학을 결합하는 방법에 대한 연구가 병행되어 왔다.
20세기 말기부터 포텐셜 이론과 유한요소법(Finite Element Method, FEM)을 결합한 연성 해석이 연구되어 왔다. Faltinsen et al. [1]은 slamming force가 작용하는 선박에 대하여 유탄성 거동 분석을 위해 구조해석에 필요한 유체력을 포텐셜 해석으로 구하였고 Euler beam equation을 이용하여 구조해석을 수행하였다. Senjanovic et al. [2]는 대형 컨테이너선에 대해 slamming과 whipping을 분석하기 위하여 스트립(strip) 이론과 FEM을 이용하여 해석하였다. 최근에 컴퓨터의 성능이 향상되면서 유체해석을 위해 점성을 고려한 N-S 방정식(Navier-Stokes’s equation)을 적용한 FSI 해석에 관한 연구가 활발하게 진행되고 있다.
여러 종류의 FSI해석 기법들에 대해서 검증이 필요하기 때문에 일반적으로 벤치마크(benchmark) 시험을 진행하게 된다. 점성이 고려된 FSI해석의 경우 전방에 원형 또는 사각형 단면의 물체를 배치하고 후방에는 탄성을 가진 얇고 긴 물체를 배치한 형태를 보편적으로 사용하고 있다. 이런 형태의 시스템은 고정된 전방의 물체를 통해 와류를 생성하고 와류는 탄성을 가진 후방의 물체에 힘을 가하게 되며 후방의 물체는 주기적으로 생성되는 와류에 의해 날개짓(flapping) 운동을 하게 된다. Wall et al. [3]는 arbitrary Lagrangian–Eulerian(ALE)을 기반으로 CFD와 FEM을 연성하여 유입구 부근에 사각단면을 가진 물체(bluff body)를 설치하고 그 후면에 탄성을 가진 얇은 평판을 부착하여 FSI 해석을 진행하였다. Turek et al. [4]는 원형 단면의 후면에 탄성을 가진 평판을 부착한 모델을 사용하여 CFD와 FEM을 연성하여 개발한 코드에 대해서 검증하였다. 또한 평판과 유체의 물성치, 격자수 그리고 시간 간격을 조절하여 나타난 결과들을 비교분석 하였다. 그 후에 Turek et al. [5]은 동일한 벤치마크 모형에 대해 하나의 도메인에서 유체와 구조 해석을 함께 해석하는 방법인 모노리틱(monolithic) FEM기법을 사용하여 결과를 비교하였다. Breuer et al. [6]는 FSI 해석 시스템에 대하여 Turek et al. [4]에 사용된 모델을 가지고 검증하였다. 그리고 동일한 시스템에서 유체 특성을 난류로 변경한 후 LES 모델을 사용하여 대상물 주위의 유동을 관찰하였다.
수치적 접근을 통한 검증뿐만 아니라 실험적으로도 많은 검증이 이루어졌다. Lienhart et al. [7]은 회전하는 실린더와 뒷면에 박막의 판과 판의 끝에 매달린 작은 추로 구성된 대상물에 대하여 particle image velocimetry(PIV)로 물체의 변위와 물체 주변 속도장을 계측하였다. Kalmbach et al. [8]는 3차원 속도 측정 시스템(3D PIV)으로 Turek et al. [4]의 벤치마크 모형을 이용하여 가시화하고 평판의 움직임과 주변 유동의 속도 분포를 계측하였다. 또한 Kalmbach et al. [9]은 동일한 Turek et al. [4]의 FSI 모델과 동일한 계측 시스템을 사용하여 레이놀즈수가 30,470인 난류에서의 유동 특성 및 평판의 거동을 분석하였다. 그 후 De Nayer et al. [10][11]가 LES 모델을 사용하여 Kalmbach et al. [9]이 실험한 결과와 비교하고 그 결과를 분석하였다.
본 논문에서는 대상물의 형태와 거동이 복잡한 문제에 대하여 FSI해석을 진행하기에 앞서 앞으로 사용될 해석 시스템에 대하여 벤치마크 시험을 진행하고 해석시스템에 대한 검증(verification)을 진행하였다. 그리고 유체해석에서 사용하는 격자는 물체가 변형할 때 물체주변의 격자도 함께 변형하게 되고 시간에 따라 변형된 격자들은 격자의 질을 평가하는 뒤틀림(skewness), 종횡비(aspect ratio), 평활도(smoothness) 등의 항목에 따라 해의 안정성과 정확성에 영향을 주게 된다. 특히 큰 변형을 가지는 FSI 해석에서는 매 시간간격마다 격자가 변하게 되고 이는 해에 영향을 주기 때문에 격자 변형에 의한 영향을 최소화하는 것이 필요하다. 대상물 주변의 격자는 대상물의 변형과 함께 변형되어야하기 때문에 변형 후 격자의 질을 유지하기 위해 변형되는 격자수를 최소화할 필요가 있다. Paik et al. [12]은 롤링탱크(rolling tank)에 설치된 탄성판을 대상으로 유체의 움직임에 의한 탄성판의 변형을 모사하기 위하여 중첩격자 시스템을 도입하였고, 이 방법이 변형이 큰 물체에 대한 해석 방법으로서 효과가 있는 것을 보여주었다. 따라서 본 연구에서는 중첩격자를 사용하여 격자 변형을 최소화한 방법과 중첩격자를 사용하지 않고 모든 격자가 변형되도록 한 방법이 해석결과에 어떠한 영향을 미치는지 분석하였다.
FSI해석 방법은 STAR-CCM+에 의한 점성 유체해석과 Abaqus에 의한 구조해석을 독립적으로 수행하고 그 결과를 매 내부 반복계산(inner iteration)에서 서로 연성하는 방법을 사용하였다. 결과 검증을 위해 Turek et al. [4]이 벤치마크 시험에 적용한 실린더 후면에 탄성을 가진 평판을 부착한 FSI3 모델을 사용하였다. 그리고 동일한 모델을 대상으로 본 논문과 유사한 FSI해석 방법을 적용한 Breuer et al. [6]의 결과도 함께 비교하였다. 이 두 가지 방법에 대해서 변위 x와 z, 양력과 항력을 비교하였고 유동장을 관찰하기 위하여 물체표면의 압력분포와 와도분포를 각각 비교하였다.
2. 수치해석 대상
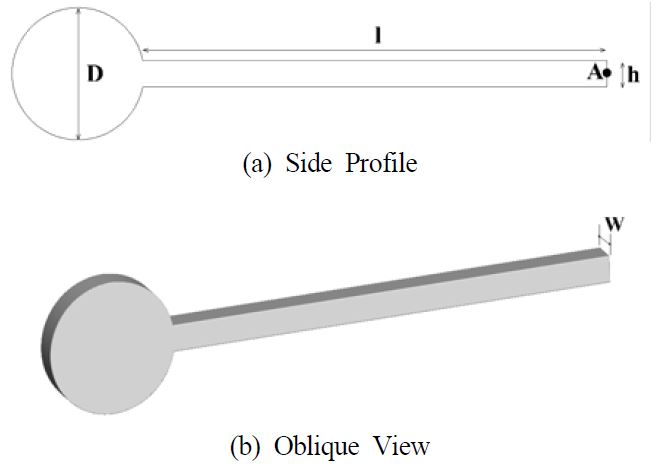
Turek et al. [5]의 FSI3 모델을 사용하였다. 층류 채널유동이며 대상물에서 유입구와 배출구간의 거리도 동일하게 설정하였다. 대상물은 Figure 1과 같이 실린더와 평판으로 이루어져 있다. 재원은 D = 0.1 m, l = 0.35 m, h = 0.02 m, w = 0.02 m이고 전체 0.45 m 길이의 대상물이다.
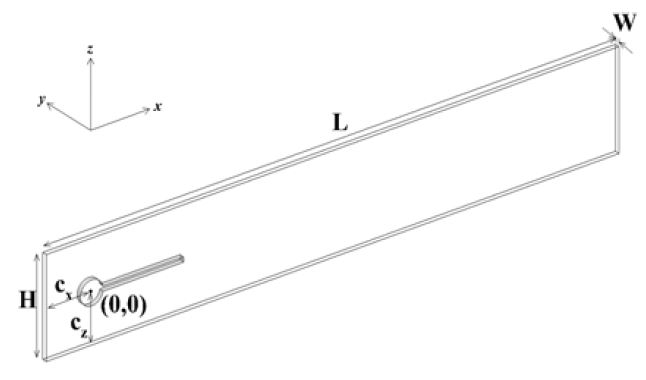
채널유동의 영역은 Figure 2에 표시하였다. 여기서 H = 0.41 m, L = 2.5 m, W = 0.02 m이다. 실린더 중심을 원점(0, 0, 0)으로 설정하였고, 원점에서 유입구까지의 x방향 거리는 Cx = 0.2 m, 바닥에서 원점까지의 z방향 거리는 Cz = 0.2 m이므로 채널 상하로 비대칭적 유동이 발생한다. 유동은 x축의 양의방향으로 수평하게 유입되며 우수 좌표계를 사용하였다. FSI3의 물성치는 아래 Table 1에 표시하였다.
3. 수치해석
3.1 유동해석
Computational fluid dynamics(CFD) 해석에는 상용프로그램인 STAR-CCM+ v10.04를 사용하였다. 레이놀즈수가 200인 층류유동이기 때문에 N-S 방정식을 직접 풀게 되고 층류 경계층을 직접 모사해야한다. 따라서 Qu et al. [13]가 제시한 층류의 경계층 두께인 δ/D≃0.001를 사용하여 경계층을 모사하였다. 여기서 δ/D는 실린더 직경(D)으로 무차원화 한 경계층 두께이다. 물체 주변의 격자가 변형 시 높은 종횡비로 인하여 격자의 질이 급격히 나빠지고 이로 인하여 수치해석에 악영향을 줄 수 있기 때문에 경계층 모사에 대한 격자 개수 및 스트레칭 계수는 종횡비가 0.05보다 작지 않도록 조절하였다.
지배방정식은 연속방정식과 비압축성 N-S 방정식을 사용하고 다음과 같은 식으로 표현한다.
| (1) |
| (2) |
여기서 U i = (U,V,W)이고 xi = (x,y,z)의 방향에 대한 유속을 나타낸다. P, ρ, μ는 순서대로 압력, 밀도, 점성계수를 나타낸다.
대류항에 대한 이산화는 2차 상류차분법을 사용하였고, 확산항에 대한 이산화는 2차 중앙차분법을 사용하였다. 시간 이산화는 2차 음해법(implicit)을 사용하여 연성과정에서 시간에 대한 정확도를 높이고자 하였다. 속도-압력 연성은 SIMPLE(semi-implicit method for pressure linked equations)을 적용하였다.
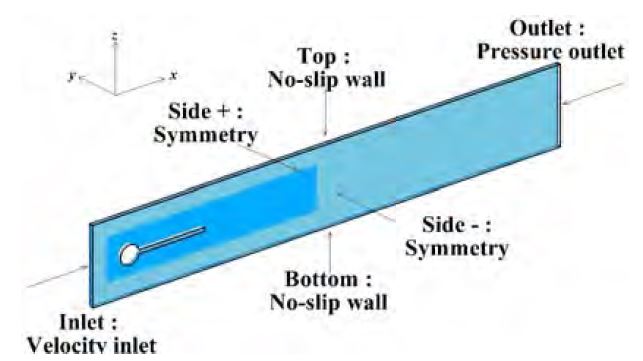
3차원 유한체적 격자에서 폭을 매우 좁게 하여 2차원 효과를 주었다. 채널 유동이므로 상단(top)과 바닥(bottom)에는 점착(no-slip)조건이 들어가고 유입구에는 속도유입조건인 velocity inlet, 배출구에는 압력이 배출구의 속도에 의해서만 결정되도록 하는 유출조건인 pressure outlet 조건을 주었다. 대상물에도 점착조건이 주어지며, 모든 점착조건에 경계층을 모사할 수 있도록 격자를 분포하였다. 전체적인 구성을 Figure 3에 표현하였다.
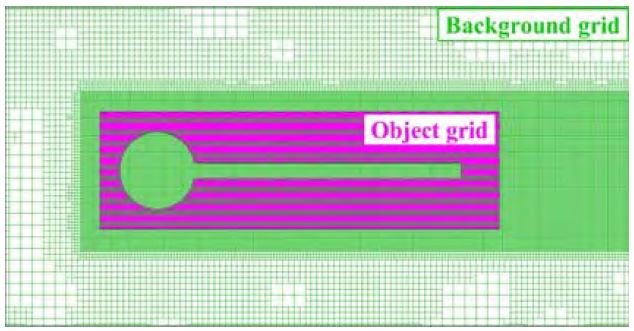
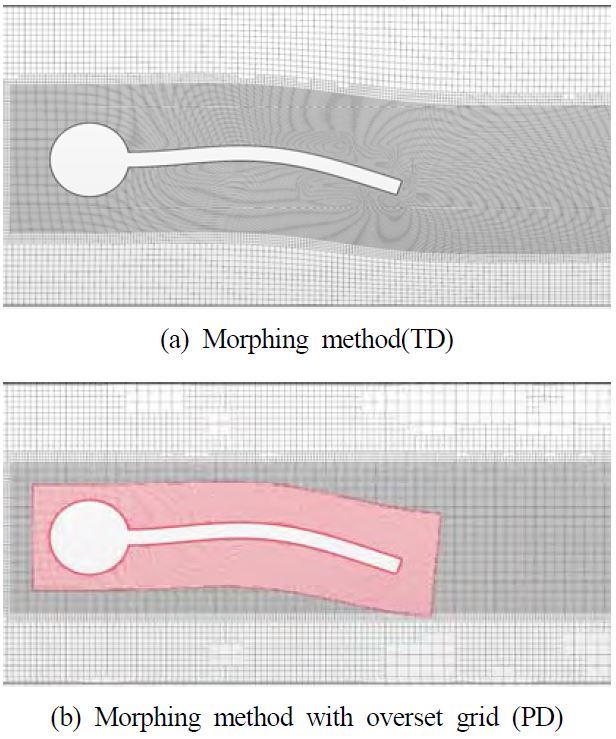
격자 시스템은 단일 격자계안의 모든 격자가 변형에 관여하도록 하는 방법(total deformation, TD)과 중첩격자를 사용하여 배경격자계와 대상격자계로 나눈 뒤 대상격자계에만 격자가 변형하도록 하는 방법(partial deformation, PD)으로 나누어 비교하였다. PD의 경우 배경격자 구성은 TD와 유사하나 대상격자계는 물체를 포함하도록 하여 배경격자계에 겹친 형태인 Figure 4와 같이 구성하였다. 대상격자계 안으로 겹치는 배경격자계의 격자들은 제외격자(dead cell)가 되어 해석에 관여 하지 않은 상태가 되고 대상격자계의 경계면에 겹치는 배경격자계의 격자들은 서로 공유 혹은 보간하게 된다.
유입구에 유입되는 속도는 Turek et al. [4]과 동일하게 포물선(parabolic) 형식의 속도분포를 적용하였다.
| (3) |
여기서 H는 채널의 높이이고 z는 유입구에 해당하는 경계면 격자의 z좌표이다.
3.2 구조해석
대상물의 구조해석을 위하여 FEM 해석 프로그램인 Abaqus 6.14-2를 사용하였다. 요소는 각각 질점 당 3개의 자유도를 가지는 8개 노드(node)로 구성된 고체요소(C3D8R)를 사용하였다.
전체좌표계에서 요소방정식을 표현하면 다음과 같다.
| (4) |
여기서 F는 전체좌표계에서의 절점 하중 벡터이고, K는 대상물의 전체좌표계에서의 강성행렬을 나타낸다. d는 각 절점의 자유도에 대응하는 변위 매트릭스이다. 시간에 대한 운동방정식은 다음과 같이 정의한다.
| (5) |
여기서 M은 전체좌표계에서 질량 매트릭스, C는 전체좌표계에서 감쇄 매트릭스를 나타낸다. 위의 운동방정식은 직접적분법(Direct integration method)인 modified Newmark’s β-family 방법을 사용하여 계산하였다. 대상물의 변형 특성을 고려하기 위하여 비선형 거동을 고려하였다.
3.3 구조-유체 연성방법
각각의 독립적인 도메인을 사용하여 연성할 때 연성기법은 중요한 요소이다. 일반적으로 유체해석을 통한 동유체력(hydrodynamic force)이 구조해석의 하중으로 작용하고 이에 따라 발생하는 구조적 응답이 변위 성분으로 유체 해석의 대상물 주위의 격자 변형으로 이어지게 된다. 대상물의 변형에 의해 유동해석에 미치는 영향이 크기 때문에 쌍방 연성(two-way coupling)을 사용하고 시간 연성에는 동일한 시간 안에서 내부 연성(implicit coupling)을 하도록 수행하였다.
Figure 5에 붉게 표시된 면이 연성을 하는 공유 면이 된다. 이 면을 통하여 유체해석과 구조해석에서 필요한 정보를 서로 교환 하게 된다. Table 2는 유동해석과 구조해석에서 공유면을 통해 필요한 정보를 공유하는 입력값과 출력값을 나타낸다.
3.4 격자변형
본 논문에서는 두 가지의 격자 변형 방법을 사용하여 결과를 비교하였다. 구조응답에 맞추어 유체영역 격자를 변형하기 위한 방법으로 모핑 기법을 사용하였다. 이는 격자의 재생성 혹은 제거가 없이 각 단위 시간별 물체의 변형에 따라 물체 주변 격자 모두를 변형만 시키는 방법이다. TD는 모핑을 격자계 전체에 적용하고 모든 경계조건 중에서 판에 해당하는 면을 제외한 모든 면은 고정되어 있다. PD는 배경격자계의 모든 면은 항상 고정되어 있고 대상격자계만이 물체의 변형에 따라 모핑 기법에 의해 변형된다. 이 때, 대상격자계에서 실린더 면을 제외한 모든 면은 자유롭게 변형될 수 있다. Figure 6에는 판의 변위가 가장 큰 지점에서의 격자 형태를 나타내었고 각각의 방법이 격자 변형에 어떤 영향을 미치는지를 나타내고 있다.
4. 결과 및 고찰
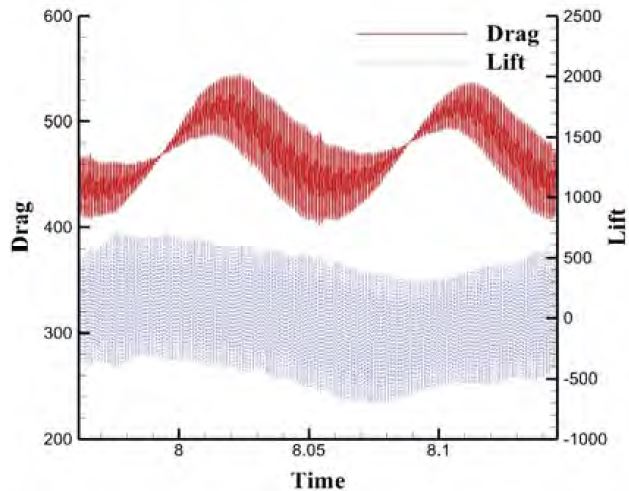
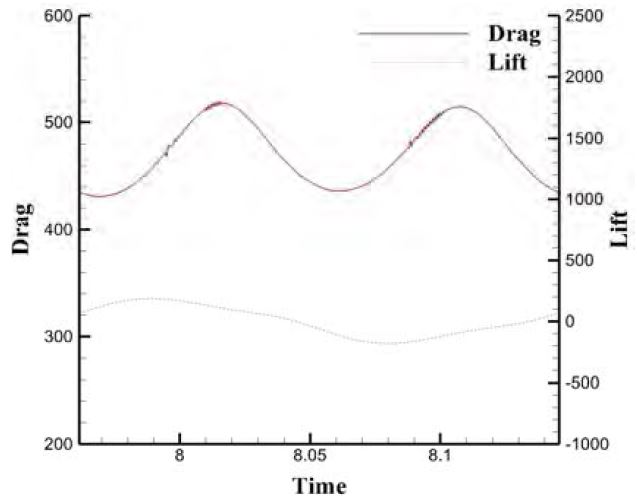
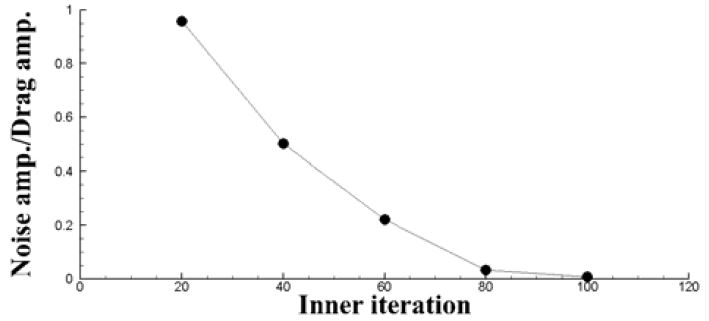
TD와 PD를 모두 동일한 조건으로 해석할 경우 TD는 Figure 7과 같이 매우 불안정한 수치적 노이즈가 발생하는 것을 볼 수 있다. 이 노이즈는 CFD만의 해석에서는 발생하지 않은 문제로 구조해석과 연성할 경우에 발생하게 된다. 노이즈를 제거하기 위해 여러 가지 방법들을 추가 할 수 있지만, 중첩격자 방법을 사용하는 PD에서는 발생하지 않은 문제이므로, 두 해석조건을 최대한 동일한 조건에서 비교하기 위해 내부 반복계산(inner iteration)량만을 조절하여 최대한 노이즈를 제거하였다. 내부 반복계산량을 증가시켜가며 노이즈를 제거하였고, Figure 9에 보는바와 같이 80이 넘어가면서부터 큰 폭으로 노이즈가 작아지는 것을 확인할 수 있다. 하지만 내부 반복계산량이 너무 클 경우 해석시간이 길어진다. 이는 경제적이지 않다고 판단하여 소량의 노이즈는 있지만 해석과 결과분석에는 문제없는 조건인 내부 반복계산량을 80으로 한 Figure 8의 결과를 가지고 분석하였다. 동일한 조건의 해석에서 내부 반복계산량이 증가되었기 때문에 해석 시간이 증가하게 된다. 양력의 한 주기에 대한 해석시간은 다음의 Table 3과 같다. 계산 시간이 TD가 PD에 비해서 약 4배 정도 증가하는 것을 확인 할 수 있고 PD가 확실히 계산시간이 줄어든 것을 확인할 수 있다. 이는 내부 반복계산량이 기존의 20에서 80으로 4배 증가하였기 때문에 생기는 계산량보다 중첩격자방법을 사용할 때 추가로 소요되는 계산량이 훨씬 작다는 것을 보여준다. 수치해석에는 동일한 컴퓨터를 사용하였고 STARCCM+ 계산에는 20 코어를 사용하고 Abaqus 계산에는 4 코어를 사용하여 동일 조건으로 계산하였다.
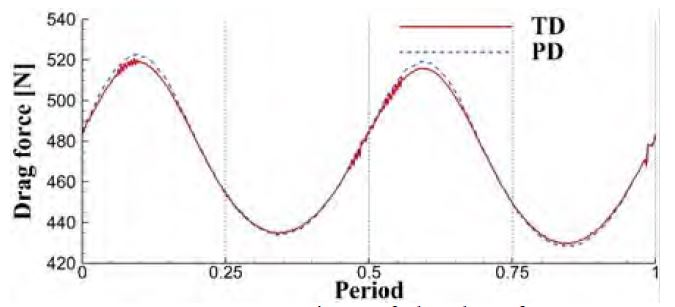
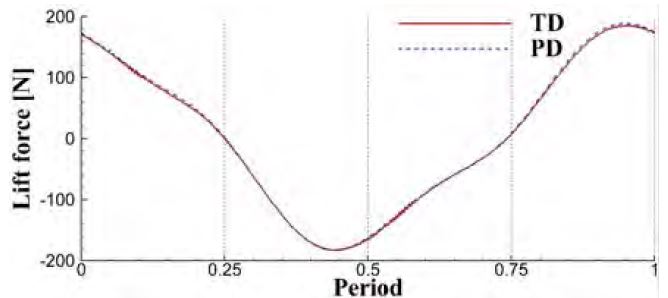
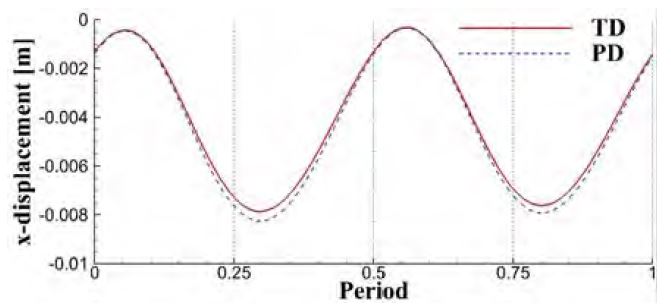
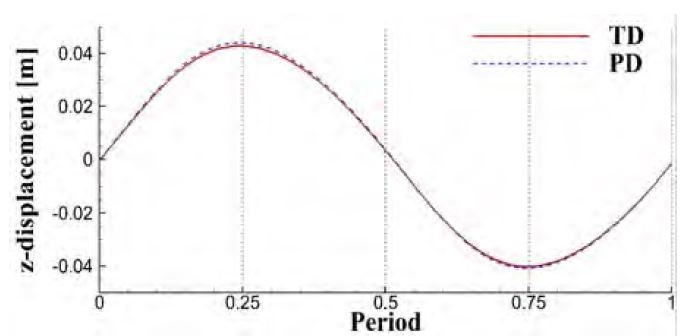
격자 구성의 차이에 따라 힘과 변위들이 어떻게 변하는지 양력의 주기를 기준으로 하여 시간 변화에 따른 결과를 Figure 10 ~ 13에 비교하였다. 여기서 양력과 항력은 실린더와 평판의 모든 면적에 대한 힘을 나타낸다. 변위는 Figure 1의 (a)에 보는바와 같이 평판의 끝단에 위치한 점 A의 변위를 관찰하였다.
두 해석방법에 의한 결과들을 시간에 따라 비교하였고 모든 결과들은 유사한 것으로 나타났다. 항력과 x변위, 양력과 z변위는 서로 유사한 주기를 보이는데 이는 서로 상관관계에 있는 것을 예상할 수 있다. Figure 11과 Figure13을 보면 z변위가 최대와 최소가 되는 시간에 양력은 변곡점이 생기는 것을 확인할 수 있다. 이는 실린더의 양력과 z변위에 따라 생성되는 평판의 양력과의 위상차로 인하여 변곡점이 생기는 것으로 판단한다. x와 z의 변위가 최대와 최소가 되는 시간이 서로 다른 것을 보인다. 이는 z변위가 최대 혹은 최소가 되기 전에 평판의 임의의 위치에서 또 다른 변형이 발생하고 있는 것을 보여준다.
수치적인 결과로 비교하기 위하여 Turek et al. [4]의 논문과 같은 방식으로 평균값을 최대와 최소의 합을 2로 나누어 정의하고 진폭은 최대와 최소의 차를 2로 나누어 정의하였다. Table 4는 각 물리량의 최고와 최저를 나타내고 Table 5은 각 물리량의 평균값과 진폭을 나타내었다. FD는 항력 [N], FL은 양력 [N], Ux는 x변위 [m], Uz는 z변위 [m], f1은 Ux의 주파수 [Hz]이고 f2는 Uz의 주파수 [Hz]이다. Table 5의 결과를 보면 힘들의 평균값과 진폭이 Breuer et al. [6]과 유사한 것을 볼 수 있다. 양력에서 평균값과의 차이가 있는 것으로 보이나 이는 양력의 진폭의 절대치와 비교할 때, 상당히 작은 값임을 알 수 있다. 물체의 변위를 간접적으로 알 수 있는 Table 4의 f2 값 또한 비슷하게 나타났다. Turek et al. [4]의 결과와 비교하면, Table 4의 f1와 f2의 주파수 결과들은 상당히 유사하게 나타나는 것을 볼 수 있다. 반면에 힘과 변위의 값들에서는 차이가 있는 것을 확인 할 수 있다. 특히 평균값보다는 진폭에서 큰 차이를 보이고 있는데, 본 연구 결과와 Breuer et al. [6]의 결과보다 작게 나타나는 경향을 가진다. Turek et al. [4]의 논문에서는 격자를 이용한 경계층 모사를 하지 않았기 때문에 와류를 제대로 구현하지 못하였고, 약해진 와도의 세기로 인하여 판을 변형하도록 하는 힘이 적어지게 된다. 따라서 이 현상이 변위의 진폭이 작아지고 이에 따라 변하는 양력과 항력의 진폭 또한 작아지게 되는 원인이라고 판단된다.
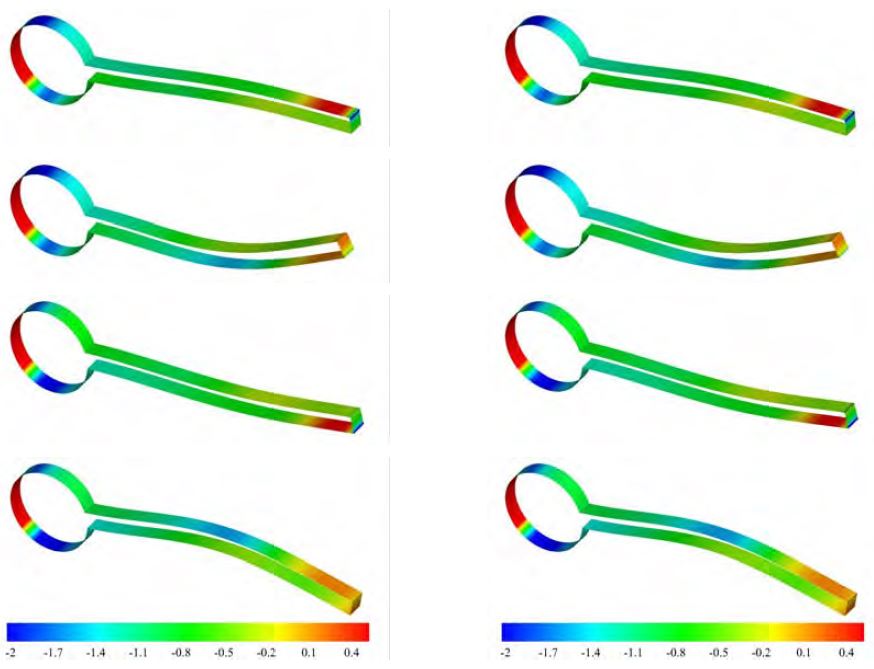
Figure 14에 와도 분포를 나타내었고 양의 값은 실선이고 음의 값은 점선으로 표현하였다. 주기에 따라 벽에 가까운 부분의 와도의 형상은 조금 차이가 있지만 물체와 가까운 위치의 와도 형상은 거의 유사한 것을 볼 수 있다. 표면에 작용하는 압력은 아래의 식을 사용하여 무차원 하였고 평판에 작용하는 압력이 실린더에 비해 상대적으로 작기 때문에 양의 등압선 값을 낮추어 상대적으로 판의 등압선을 짙게 표현하여 Figure 15에 나타내었다.
| (6) |
물체 표면 압력을 살펴보면 주기가 0.50T일 때 판의 모서리 부분에서 조금의 차이는 있지만 전체적인 주기별 압력 분포는 거의 유사함을 알 수 있다.
격자 변형 방법 간의 차이를 자세히 보기 위하여 물체표면 압력과 와도분포를 살펴보았고, 주기적인 해석 결과들을 fast Fourier transform(FFT)를 이용하여 조화해석을 진행하여 주파수, 진폭 그리고 위상각에 대해서 결과를 Table 6 ~ 9에 비교하였다. 3차 이상부터의 성분은 결과에 미치는 영향이 미비하기 때문에 나타내지 않았다.
Table 6 ~ Table 9의 결과를 보면, 항력과 x변위 그리고 양력과 z변위는 2차까지의 주파수가 동일한 것으로 보아 서로 상관관계에 있다고 보인다. 또한 항력에 비해 양력은 2차 성분의 영향이 큰 것을 확인 할 수 있다. 이는 앞에서 보인 Figure 11에서도 뚜렷하게 나타난다. 두 방법 모두 주파수는 일치하며 진폭과 위상차도 유사함을 알 수 있다.
5. 결 론
본 연구에서는 FSI 문제에 대해서 Turek et al. [4]의 모델을 사용하였고 중첩격자 방법과 모핑 기법을 사용하여 격자변형 방법에 따라 해석결과에 미치는 영향을 살펴보았다.
우선 중첩격자를 사용하지 않을 때, TD는 동일한 조건에서는 내부 반복계산을 4배 이상 많이 가져가야 노이즈를 제거 할 수 있고 이렇게 할 경우 중첩격자 기법을 추가하더라도 4배정도의 시간이 더 소요됨을 알 수 있다. 평판의 x변위에 따른 항력의 크기는 전체 항력에 큰 영향을 주지 않지만 평판의 z변위에 따라 생성되는 양력의 영향력은 전체 양력에 영향을 주는 것을 알 수 있다. 이는 실린더에서 생성되는 양력과 평판에서 생성되는 양력의 위상이 서로 차이가 나고 평판의 양력이 상대적으로 크기 때문에 양력의 시간 그래프에 변곡점이 나타나는 것을 볼 수 있으며 이는 FFT 결과를 통해서도 확인 할 수 있다. 그리고 z변위와 x변위의 변곡점의 위치가 차이나는 것을 확인 할 수 있는데, 이는 z변위가 최대가 되기 전에 평판의 임의의 지점에 또 다른 변형이 발생한다는 것을 보여주고 있다.
두 격자시스템의 결과들을 수치적으로 결과를 분석하였을 때, 주파수는 동일하였고 나머지 물리량도 거의 유사한 것으로 확인하였다. 유동장의 와도형상과 물체 표면의 압력을 살펴보더라도 결과의 차이가 거의 없는 것으로 나타났다. 결론적으로 두 해석 방법에서 결과의 차이가 거의 없었다는 점을 고려하면 안정적인 수렴과 해석 시간에서 중 첩격자 방법을 함께 사용하는 것이 FSI해석에 더 유리 할 것으로 판단한다. 이는 강체변위가 큰 운동일수록 더 큰 효과가 있을 것으로 예상된다.
후 기
이 연구는 2011년도 정부(미래창조과학부)의 재원으로 한국연구재단의 지원(No.2011-0030013)과 산업통상자원부 해양플랜트특성화대학의 지원으로 수행된 과제이며 이에 감사드립니다.
References
-
O. M. Faltinsen, “The effect of hydroelasticity on ship slamming,”, Philosophical Transactions of The Royal Society A Mathematical Physical and Engineering Sciences, 355(1724), p575-591, (1997).
[https://doi.org/10.1098/rsta.1997.0026]

- I. Senjanovic, and J. Parunov, “Slamming and whipping aalysis of large container ship,”, The Eleventh International Offshore and Polar Engineering Conference, (2001).
- W. A. Wall, and E. Ramm, “Fluid-structure interacation based upon a stabilized(ALE) finite element method. Comutational mechanics,”, 4th World Congress on Computational Mechanics: New Trends and Applications, (1998).
-
S. Turek, and J. Hron, “Proposal for numerical benchmarking of fluid-structure interactions between an elastic object and laminar incompressible flow,”, Fluid-Sturcture Interaction, Springer, Heidelberg, (2006).
[https://doi.org/10.1007/3-540-34596-5_15]

- S. Turek, J. Horn, M. Razzaq, H. Wobker, and M. Schafer, Numerical Benchmarking of Fluid-Structure Interaction: A Comparison of Different Discretization and Solution Approaches, Fluid-Sturcture Interaction Ⅱ-Modelling, Simulation, Optimization, Heidelberg: Springer, (2010).
-
M. Breuer, G. De Nayer, M. Munsch, T. Gallinger, and R. Wuchner, “Fluid-structure interaction using a partitioned semi-implicit predictor-corrector coupling scheme for the application of large-eddy simulation,”, Journal of Fluid and Structures, 29, p107-130, (2012).
[https://doi.org/10.1016/j.jfluidstructs.2011.09.003]

- H. Lienhart, and J. P. Gomes, “Experiment study on a two-dimensional fluid-structure interaction reference test case,”, ECCOMAS CFD 2006: Proceedings of the European Conference on Computational Fluid Dynamics, (2006).
- A. Kalmbach, and M. Breuer, “Investigations on fluid- structure interactions using volumetric particle-image velocimetry,”, 16th International Symposium on Applications of Laser Techniques to Fluid Mechanics, (2012).
-
A. Kalmbach, and M. Breuer, “Experimental PIV/V3V measurements of vortex-induced fluid-structure interaction in turbulent flow-A new benchmark FSI-PfS-2a,”, Journal of Fluid and Structures, 42, p369-387, (2013).
[https://doi.org/10.1016/j.jfluidstructs.2013.07.004]

-
G. De Nayer, and M. Breuer, “Numerical FSI investigation based on LES: Flow past a cylinder with a flexible splitter plate involving large deformations (FSI-PfS-2a),”, International journal of Heat and Fluid Flow, 50, p300-315, (2014).
[https://doi.org/10.1016/j.ijheatfluidflow.2014.08.013]

- G. De Nayer, A. Kalmbach, M. Breuer, S. Sicklinger, and R. Wuchner, “Flow past a cylinder with a flexible splitter plate: A complementary experimental-numerical investigation and a new FSI test case (FSI-PfS-1a),”, Computers & Fluids, 99, p18-43, (2014).
-
K. J. Paik, and P. M Carrica, “Fluid-structure interation for an elastic structure interacting with free surface in a rolling tank,”, Ocean Engineering, 84, p201-212, (2014).
[https://doi.org/10.1016/j.oceaneng.2014.04.016]

-
L. Qu, C. Norberg, L. Davidson, and S. H. Peng, “Quantitative numerical analysis of flow past a circula cylinder at Reynolds number between 50 and 200,”, Journal of Fluids and Structures, 39, p347-370, (2013).
[https://doi.org/10.1016/j.jfluidstructs.2013.02.007]