Numerical analysis of a channel flow with two tubes in a vertical plain-fin type heat exchanger
Copyright ⓒ The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
Natural convection heat transfer in a channel flow is investigated to determine the maximum performance of a plain-fin type heat exchanger with two tubes. A vertical channel flow with isothermal heated surfaces is evaluated using Rayleigh numbers, the plate-fin aspect ratios, and pitches between two vertical plates. The channel flow had two horizontal heated tubes. The finite volume method was selected as a numerical tool. When W, the dimensionless ratio between the height and width of the plate, was changed from 1.0 to 0.8, the heat-dissipation performance increased. At small Rayleigh numbers, the dimensionless plain-fin ratio was not an important factor. In the cases of different geometry ratios with the same plain-fin area, the heat dissipation rate increased when the horizontal length increased. On the same-volume basis, the total heat transfer rates increased. Thus, smaller pitches are recommended when considering the flow pattern. Finally, the optimum design arrangements are suggested to obtain the maximum thermal performance in a plain-fin type heat exchanger.
Keywords:
Channel flow, Computational fluid dynamics, Heat exchanger, Plain-fin1. Introduction
Natural convection heat transfer occurs, without external in-puts, in a thermal system. This means that this cooling technique is a reliable and sustainable method, and will operate without restriction. However, thermal efficiency is very low compared to forced convection or two-phase heat transfer processes, such as boiling and condensation. Therefore, a thermal system design that utilizes natural convection needs to be highly efficient and reliable. Vertical plain-fins are commonly used to improve heat transfer in a heat generating system. Huang et al. [1] presented natural-convection enhancement from horizontal rectangular-fin arrays. They showed that the perforation in the inner part of fins showed the best improvement in terms of ventilation and heat transfer performance. Oosthuizen and Paul [2] conducted a natural-convection numerical study for a narrow vertical flat plate at a constant temperature. The plate between the plain-fins had a significant influence on natural-convection heat transfer. They suggested that, with a decreasing Rayleigh number, natural-convection increases. Ahmadi et al. [3] presented an analytical natural-convection analysis for isothermal, vertically mounted rectangular fins. Their proposed model showed good correlation between numerical and experimental results. They reported the semi-analytical, local, and average Nusselt numbers as functions of the Rayleigh number, temperature difference, and fin aspect ratio.
Plain-fins in a heat exchanger with a single tube are com-monly used in air cooling, refrigeration, and HVAC systems. Nemati et al. [4] presented the numerical investigation of natural convection over an annular-finned horizontal cylinder. They suggested several parameters for analyzing and correlating the average Nusselt number, and gave optimum fin spacing as a function of the Rayleigh number. Yildiz and Yundu [5] dis-cussed the experimental results on the performance of annular fins on a horizontal cylinder, in free convection heat transfer. They used scale analysis in order to estimate the optimum fin spacing, and proposed that the correlation could be generalized by applying the order of magnitude. Chen et al. [6] investigated the natural-convection characteristics of vertical plate-fins heat exchangers, with various tube diameters. They reported good correlation between the Nusselt and the Rayleigh numbers.
In this study, we analyze the performance of vertical plate-fins in a heat exchanger with two tubes. First, two narrow vertical plates, in natural convection, were selected for a comparative study. A confined geometry with two tubes is then studied with a view to enhancing the heat dissipation performance in a heat exchanger, as part of a crevice-type heat pipe system. In order to determine the optimal heat transfer parameters, the Rayleigh number, the plate-fins height-width aspect ratio, and the spacing in the vertical plate fins are investigated.
2. Mathematical modeling
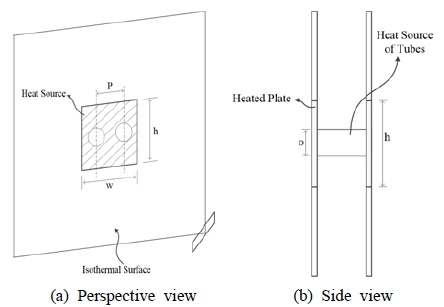
The schematic of a whole plate-fin heat exchanger is shown in Figure 1[7]. This type of cooling heat exchanger is located in the condensing section of a crevice-type heat pipe. In this ther-mal system, a passive heat-dissipation method, natural heat con-vection, is used. This is an inefficient cooling method compared to an active method. Thus, a small increase in efficiency is an important design parameter. The entire heat exchanger domain is extremely large to investigate the optimum parameters of plain-fins and horizontal tubes in a channel flow. The domain is there-fore reduced to the computational geometry of two circular tubes between two vertical plates. The vertical plain-fins for the com-putational calculation are shown in Figure 2 (b).
In the computational domain, the flow is assumed steady and laminar. The fluid properties are constant, except for density, which is a function of temperature. To obtain the dimensionless governing equations, the following dimensionless variables are defined [2]:
where, h is the height of the vertical heated plate, Th is the uniform surface temperature of the heated plate, T∞ is the far-field fluid temperature, and P is the pressure. In the above equa-tions, the following reference velocity is introduced:
where α is the thermal diffusivity, Pr, and Ra are the Prandtl and Rayleigh numbers and are defined as
In terms of dimensionless variables, the governing equa-tions, namely the conservation of mass, momentum, and energy equations of natural convection are as follows:
| (1) |
| (2) |
| (3) |
where Ui, P, T and δij are the dimensionless velocity com-ponents, dimensionless pressure, dimensionless fluid tempera- ture, and Kronecker delta, respectively.
For velocity profiles, both the walls and the tube surfaces have no-slip conditions. For temperature profiles, the heated surfaces are assumed to be at a constant temperature. Thus, all heated surfaces including the tube surfaces, are applied as the Dirichlet boundary conditions, and the extra-symmetrical vertical walls and upper surface are applied as the Neumann boundary conditions.
For computational analysis, the finite volume element of ANSYS Fluent is used for natural-convection heat transfer and fluid-flow calculations [8]. In the fluid-flow domain, the pressure spatial discretization uses a body-force weighted scheme, and the density is approached as a Boussinesq approximation.
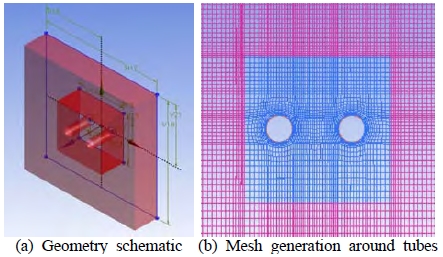
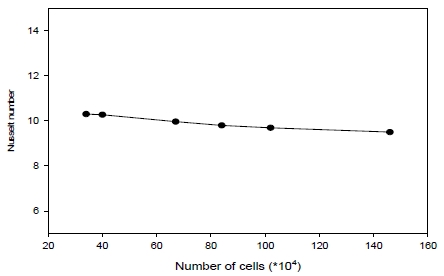
The schematic of the computational domain geometry for two vertical plain-fins is shown in Figure 3. Figure 3 (a) shows the schematic for the confined channel flow domain, which is the part of the whole plain-plate type heat exchanger. Two cylinders, with a diameter of 7.2 mm, are located symmetrically about the center. The heated plates are positioned at the end of both sides. For computational accuracy, the domain is divided into two blocks to obtain the structured grids, which are shown in Figure 3 (b). The grids are denser near the edges, and the o-grid scheme is applied around both tubes. Denser grids are also located at the upper part of the domain. These uneven grid densities are be-cause of the assumption that the flow, and heat transfer, will be highly active at the upper part due to the buoyancy force. Figure 4 shows the mesh independence with various grid numbers. Below a grid number of 600,000, the convergence decreases linearly, and, above 600,000, the convergence becomes small. Thus, approximately 600,000 grid numbers are selected for future calculations.
Before the numerical results of heat transfer characteristics of vertical plates with two tubes are presented, the simple case of the plain channel-flow geometry is investigated, to check the natural-convection comparison with various grid numbers. The correlations are Churchill's [9],
| (4) |
and Morgan's correlation [10].
| (5) |
where the Nusselt number is defined as follows.
| (6) |
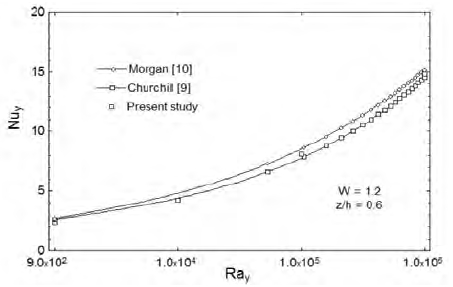
The validity of the previously obtained results is checked for further analysis. Figure 5 shows the comparison of the experimental- and numerical-Nusselt numbers with varying Rayleigh numbers. This is the case of channel flow with heated areas at the center of the plain plate. The case results show good correlation with previous results of Churchill [9] and Morgan [10].
3. Results and discussion
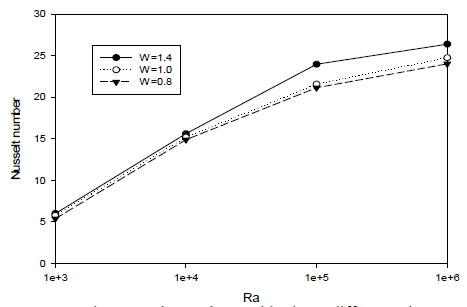
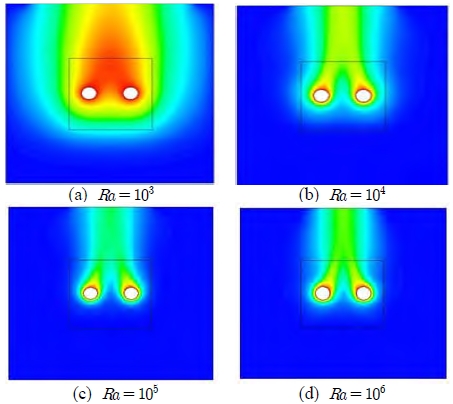
To obtain the optimum dimensional geometry of plate fins in a detailed domain, the plain-fin aspect ratio was considered. Figure 6 shows the Nusselt numbers with varying plate ratios at different Rayleigh numbers. The Rayleigh number is based on the plate height, h, and W, the dimensionless ratio given by W = w/h. The Nusselt numbers increase linearly to Ra = 105. Above that Rayleigh number, the increasing ratio decreased. At different dimensionless ratios of the heated plate, the Nusselt numbers increase to 0.24 and 0.42 at Rayleigh numbers, Ra = 103 and Ra = 104 , respectively. However, when the Rayleigh number is 105, the Nusselt number difference is approximately 2.40, which means that when W is changed from 1.0 to 1.4 at Ra = 104 , the heat dissipation increase is small. The same situation occurs even when the Rayleigh number is larger than 104. However, W changes from 1.0 to 0.8 at Ra = 105, where the heat dissipation enhancement is large. This means that at small Rayleigh numbers, the dimensionless plain-fin aspect ratio is not an important factor. However, when the Rayleigh number is large, the heat dissipation effect with smaller dimensionless ratios is important. Figure 7 shows temperature contours at different dimensionless plate ratios. At low Rayleigh numbers, heat spreads through the entire domain as shown in Figure 7 (a). As the Rayleigh number increases, the heated sec-tion is reduced because of the stronger flow patterns. This means that the buoyancy force increases with an increasing Rayleigh number. Above the two tubes, the core heat flow patterns have a slimmer shape, which indicates increased flow characteristics.
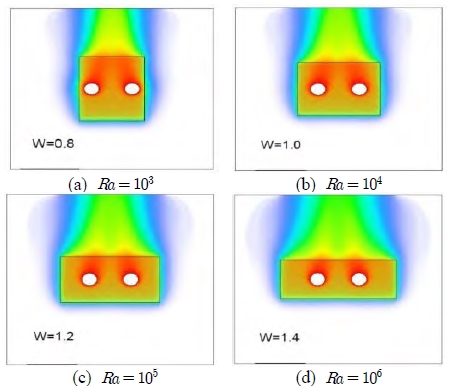
Figure 8 shows the temperature contours of the effects of varying plate geometries. The same plate area was used for all four cases, therefore, all cases have the same heat transfer areas but different widths and heights. These cases were evaluated to determine the effect of horizontal and vertical geometry on the plain-fin heat exchanger, with the same heat transfer surfaces. In all four cases, temperature distributions showed similar patterns. When the dimensionless width increased, the heated area also increased at the upper fluid domain in the horizontal direction. Table 1 presents the total heat transfer rates corresponding to Figure 8. The heat dissipation rate increased linearly when the horizontal length increased. Figure 8 (d) shows the best heat dissipation result. However, Figure 8 (c) is selected considering the confined physical geometry of Figure 1.
Figure 9 shows the temperature contours with different pitches between vertical plain-fin plates. When the pitches decrease, the temperature increases rapidly and is shown by the heated areas above the upper section of the heated plate. This temperature increase is caused by the active thermal boundary interaction between two natural convection boundary layers when the distance between vertical plain-fins is small. This effect can be seen in Figure 9 (d), which shows the temperature distributions along the centerline, in the side view. Table 2 lists the total heat transfer rates with different pitches. At pitches of 20 mm, 10 mm, and 5 mm, the total heat transfer rates are 0.78 W, 0.61 W, and 0.34 W, respectively. The total heat transfer rates decrease linearly with decreasing pitches. However, on the same-volume basis, the total heat transfer rates will be approximately 0.78 W, 1.22 W, and 1.36 W, respectively. This means that when the distance between the two vertical plates decreases, the total heat dissipation performance increases on the same-volume basis.
4. Conclusions
Natural convection heat transfer of the confined geometry in a plate-fin heat exchanger with two horizontal tubes has been investigated numerically for the laminar flow region. To get the optimum performance the various geometries are studied. The conclusions are as follows.
When the Rayleigh number is larger than 104 at the different dimensionless ratios of the heated plate, the plate-fine geometry effect is large. Especially, when W changes from 1.0 to 0.8, the changed heat dissipation is very effective. At the small Rayleigh number, the dimensionless plain-fin ratio is not important. When the geometry ratios with the same heat area varies, the heat dissipation rate increases as the horizontal length increases. When the pitch between the vertical plates decreases, the total heat transfer rates decrease. However, on the total volume basis, the total heat transfer rates increase. Thus, the pitches which is less than 10mm are recommended if geometry constriction is considered.
Nomenclature
| D : | Tube diameter | mm |
| h : | Vertical size of a plain-fin | mm |
| Nu : | Nusselt number | - |
| P : | Dimensionless Pressure | - |
| Pr : | Prandtl number | - |
| Ra : | Rayleigh number | - |
| T : | Temperature | ℃ |
| Th : | Heated plate temperature | ℃ |
| Ta : | Ambient air temperature | ℃ |
| Tw : | Tube wall temperature | ℃ |
| Ui : | Dimensionless velocity | - |
| Xi : | Dimensionless coordinates | - |
| w : | Horizontal size of a plain-fin | mm |
| W : | Dimensionless ratio | - |
| Greek Symbols : | ||
| α : | Thermal diffusivity | m2/s |
| β : | Coefficient of volume expansion | 1/K |
| Θ : | Dimensionless temperature | - |
| ν : | Kinematic viscosity | m2/s |
| δij : | Kronecker delta | - |
Acknowledgments
This work was supported by a Research Grant of Pukyong National University(2015 year).
References
-
G. J. Huang, S. C. Wong, and C. P. Lin, “Enhancement of natural convection heat transfer from horizontal rectangular fin arrays with perforations in fin base”, International Journal of Thermal Sciences, 84, p164-174, (2014).
[https://doi.org/10.1016/j.ijthermalsci.2014.05.017]

- P. H. Oosthuizen, and J. T. Paul, “Natural convective heat transfer from a narrow vertical flat plate”, Proceedings of the 9th AIAA Conf, San Francisco, CA., p1-8, (2006).
-
M. Ahmadi, M. Fakoor, and M. Bahrami, “Natural convection from vertical parallel plates: An integral method solution”, Journal of Thermophysics and Heat Transfer, 29(1), p140-149, (2015).
[https://doi.org/10.2514/1.t4308]

- H. Nemati, S. Samivand, and S. Roy, “Numerical investigaton of natural convection heat transfer over annular finned horizontal cylinder”, International Journal of Heat and Mass Transfer, 96, p330-345, (2016).
- S. Yildiz, and H. Yundu, An experimental investigation on performance of annular fins on a horizontal cylinder in free convection heat transfer, Heat and Mass Transfer, p239-251, (2004).
-
H. Chen, Y. Lin, P. Chen, and J. Chang, “Numerical and experimental study of natural convection heat transfer characteristics for vertical plate fin and tube heat exchangers with various tube diameters”, International Journal of Heat and Mass Transfer, 100, p320-331, (2016).
[https://doi.org/10.1016/j.ijheatmasstransfer.2016.04.039]

- J. S. Kim, J. Y. Bae, and E. Kim, “Analysis on the experimental cooling performance of a high power LED package with a crevice-type vapor chamber heat pipe”, Journal of the Korean Society of Marine Engineering, 39(8), p801-806, (2015).
- ANSYS Inc., Ver. 16, www.ansys.com Accessed December 1, (2015).
-
S. W. Churchill, and H. S. Chu, “Correlating equations for laminar and turbulent free convection from horizontal cylinder”, International Journal of Heat and Mass Transfer, 18(9), p1049-1053, (1975).
[https://doi.org/10.1016/0017-9310(75)90222-7]

- V. T. Morgan, “The overall convective heat transfer from smooth circular cylinder,” Advances in Heat Transferr, 11, p199-264, Academic Press, New York, (1975).