고효율 직결식 10MW급 프로펠러의 감쇠특성에 관한 연구

1. 서 론

최근에 건조되는 선박은 연료효율 증대와 안락한 운항을 목적으로 고효율 프로펠러를 부착하고 있다. 이러한 고효율 프로펠러는 프로펠러 효율향상과 진동 저감을 위해서 프로펠러 직경과 스큐각을 증가시켰다. 이와 같이 고효율 프로펠러가 탑재됨에 따라 이전의 프로펠러 특성을 고려한 프로펠러 감쇠방법을 비틀림 강제진동 해석에 적용할 경우에는 해석과 측정결과에 차이가 많이 발생하고 있다. 감쇠계수는 각 질점의 변위를 결정하는 중요한 요소이기 때문에 비틀림진동 해석 시 가장 문제로 되는 부분이다. 이에 대해서 그동안 많은 사람들에 의하여 이 문제가 다루어져 왔으나 아직도 명백한 결론은 얻지 못하고 있다.

실제 선박용 기관축계에 작용하는 감쇠요소로 고려할 수 있는 것은 기관의 각부 베어링과 피스톤의 펌프작용, 마찰저항 및 충격 등에 의한 것이나 크랭크축을 비롯한 축계재료의 히스테리시스 손실에 의한 것 등이 있다. 또한 피구동부로는 프로펠러의 감쇠작용에 의한 것, 발전기 자신의 전기적인 저항에 의한 감쇠등이 있다. 이들은 복합적으로 추진축계의 진동 감쇠의 역할을 한다. 축계 비틀림진동의 진폭과 응력을 결정하기 위해서는 앞서 언급한 감쇠작용을 아는 것이 가장 중요하나 이들 각종 감쇠를 낱낱이 정량적으로 파악하는 것은 매우 곤란하다. 따라서 이것을 기관에서 발생하는 기관감쇠, 축계에서 발생하는 히스테리시스 감쇠, 피구동부에서 발생하는 프로펠러 또는 발전기 감쇠등으로 나누어서 계산한다[1]-[3]. 기관 감쇠와 프로펠러 감쇠는 점성감쇠 즉, 속도비례형을 보고 각 질점에 직접 작용하는 절대감쇠로 다룬다. 또한 히스테리리스 감쇠는 변위비례형으로 보아 각 질점간에 작용하는 상대감쇠로 다룬다. 반면 일부에서는 축계와 관련된 모든 감쇠를 하나로 묶어서 공진배율로 평가하고 평형진폭을 이용하여 진동진폭을 계산하는 경우도 있다.

본 연구에서는 비틀림진동 해석에 적용되고 있는 각종 프로펠러 감쇠 적용방법에 따른 해석편차를 비교·검토한다. 또한 고효율 직결식 10MW급 프로펠러를 탑재한 선박을 대상으로 프로펠러 감쇠방법에 따른 해석치를 계측결과와 비교하여 현 시점에서 사용상 적절한 프로펠러 감쇠방법을 제시한다.

2. 비틀림진동 해석을 위한 프로펠러 감쇠 적용 방법 비교

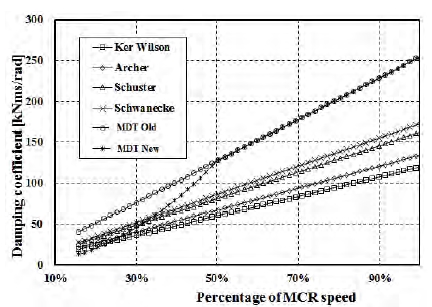
Table 1은 현재 비틀림진동 해석을 위해 주로 사용되고 있는 프로펠러 감쇠방법들을 보여주고 있다. 이들 중 Ker Wilson 및 Archer 방법은 프로펠러 순간속도에 대한 토크 변동율로 주어지는 프로펠러 감쇠특성을 이용한다[1]-[4]. 여기에 계수 α를 곱하는 형태를 취하고 있다. Schuster와 Schwanecke 방법은 비 정상류 날개이론을 이용하여 감쇠계수를 구하는 이론식이며, MAN Diesel & Turbo(MDT)의 방법은 직결형 프로펠러 감쇠를 일반적인 속도비례형 감쇠로 보고 점성감쇠계수로 감쇠를 계산하는 방법이다[3][5]-[7]. MDT의 방법은 두가지로 분류된다. MDT 과거방식(이하 MDT Old)은 위험회전수에상관없이 ζ값을 0.055로 고정하는 방법이고, MDT 신규방식(이하 MDT New)은 위험회전수가 연속최대회전수의 50% 이하에 있는 경우에 대해 위험회전수와 연속최대회전수 비에 비례하게 적용하도록 되어 있다.

Table 1:

Comparison of propeller damping methods

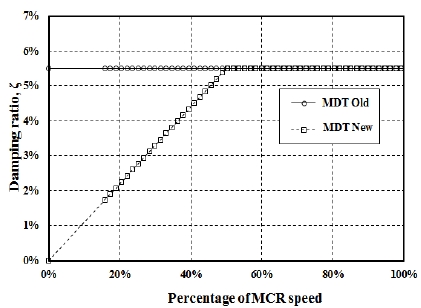
Figure 1은 Table 1에서 제시된 각각의 프로펠러 감쇠 적용방법 별로 구한 프로펠러 감쇠계수의 회전수 증가에 따른 변화를 보여주고 있다. 그림에서 보이는 바와 같이 프로펠러 감쇠계수는 프로펠러 감쇠 적용방법에 관계없이 엔진 회전수에 비례하여 증가한다. Figure 2는 MDT Old방법과 MDT New방법으로 구한 프로펠러 감쇠계수의 엔진 회전수 증가에 따른 변화를 보여주고 있다. 여타 방법에 비해 MDT New방법이 MCR 회전수의 50% 이하에서 더 급격한 기울기를 가지고 있는 것을 알 수 있다. 이는 위험회전수가 최대연속회전수의 50% 이하 범위 내에 존재하는 경우 프로펠러 감쇠계수는 회전수에 비례하여 증가하기 때문이다.

Figure 1:

Propeller damping coefficient in accordance with each propeller damping method

Figure 2:

Propeller damping ratio (MDT Old vs. New)

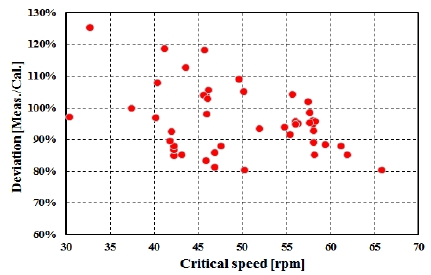
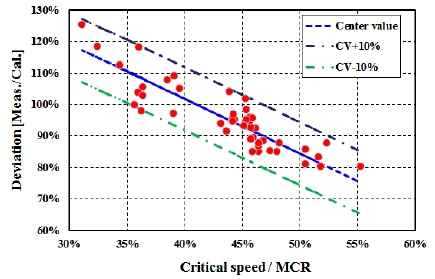
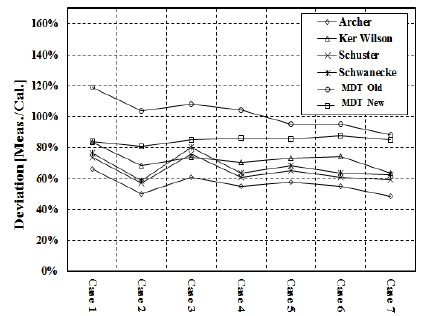
Figure 3은 위험회전수에 따른 측정치와 해석치의 비를 나타내고 있다. 그림에서 보이는 바와 같이 위험회전수가 감소함에 따라 측정치와 해석치의 비가 증가하는 경향이 있다. Figure 4는 위험회전수와 연속최대회전수(MCR) 비에 따른 측정치와 해석치의 비를 나타내고 있다. 이 그림을 검토하여 보면 위험회전수와 연속최대회전수 비가 감소함에 따라 ±10% 범위 이내에서 측정치와 해석치의 비는 커지고 있는 것을 알 수 있다.

Figure 3:

Deviation between measurement and calculation (critical speed)

Figure 4:

Deviation between measurement and calculation (critical speed/MCR)

3. 고효율 저진동 프로펠러 감쇠 특성 비교

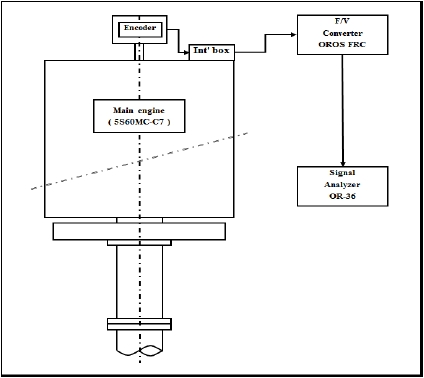
본 장에서는 고효율 직결식 프로펠러를 장착한 선박을 대상으로 프로펠러 감쇠적용 방법에 따른 감쇠특성을 비교·검토한다. Table 2는 해석 대상 예제 선박의 축계요목을 나타나며, Figure 5는 비틀림진동 계측방법을 보여주고 있다.

Table 2:

Specifications of shafting system for each case

Figure 5:

Torsional vibration measuring system

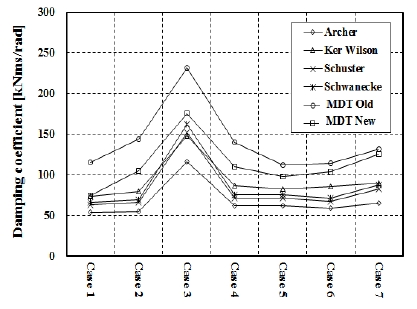
Figure 6은 Table 1에서 제시한 프로펠러 감쇠 적용방법를 적용하여 예제선박들의 프로펠러 감쇠계수를 구한 결과를 보여주고 있다. 이 그림을 검토하여 보면, 프로펠러 감쇠계수의 크기는 MDT Old > MDT New > Ker wilson > Schuster > Schwanecke > Archer 순으로 감소하고 있다.

Figure 6:

Propeller damping coefficient in accordance with each propeller damping method

Figure 7은 예제선박들을 대상으로 위험회전수에서의 비틀림진동 측정치와 해석치를 비교한 결과이다. 이 그림을 검토한 결과 MDT방법을 제외하고는 비틀림진동 측정결과값은 해석 결과보다 30%이상 낮음을 알 수 있다. 그리고 MDT New 방법은 해석치 대비 측정치가 10% ~ 20% 범위내에서 상당히 고르게 분포하고 있음을 알 수 있다. 따라서 MDT New방법이 다른 프로펠러 감쇠 적용방법들과 비교할때 해석치가 측정치에 가장 근접하다고 판단된다.

Figure 7:

Deviation between measurement and calculation at critical speed

4. 엔진 정격조정에 따른 프로펠러 감쇠특성 비교

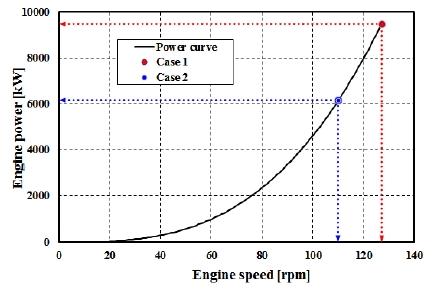
본 장에서는 엔진 정격조정에 따른 프로펠러 감쇠특성의 변화를 검토한다. 최근 건조되는 에코십은 엔진에서의 연료소비율 저감을 위해 보통 30% ~ 40%의 엔진 정격조정을 시행하고 있다[8][9]. 여기서는 엔진 정격조정에 따른 프로펠러 감쇠계수의 영향을 검토하기 위해서 정격조정된 출력과 회전수가 본래의 프로펠러 곡선을 따르는 경우에 대해서 해석을 시행하였다.

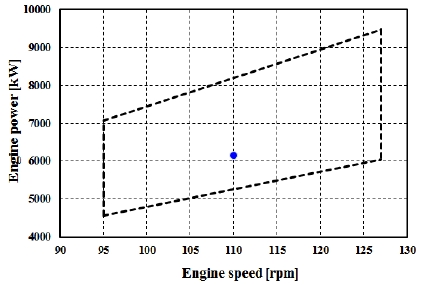
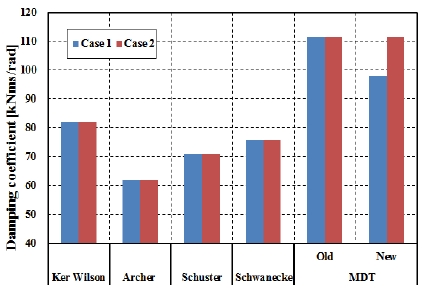
Figure 8과 Figure 9는 각각 정격조정된 출력과 회전수를 엔진 부하선도와 프로펠러 곡선상에 비교하여 나타낸 것이며, Figure 10은 엔진 정격조정 전·후의 경우에 프로펠러 감쇠 적용방법에 따른 프로펠러 감쇠계수를 비교한 것이다. 여기서 Case I은 엔진 정격조정 전의 엔진 출력과 회전수를, Case II는 정격조정된 출력과 회전수를 고려하여 구한 감쇠계수이다. 각각의 그림을 검토하여 보면 MDT New방법을 제외하고는 모든 방법들이 정격조정에 관계없이 감쇠계수가 동일한 것을 알 수 있다. 이는 MDT New방법이 Figure 2에서 보이는 바와 같이 위험회전수와 연속최대회전수 비가 50% 이하인 경우에는 회전수에 비례하여 증가하는 감쇠계수비를 적용하였기 때문이다. 하지만 MDT New방법을 제외한 다른 방법들은 엔진 정격조정에 따라 해당 축계 설계에 반영되어 있으므로 사용 상 문제가 없을 것으로 판단된다.

Figure 8:

Engine load diagram with de-rating point

Figure 9:

Power curve with de-rating point

Figure 10:

Propeller damping change with engine de-rating

5. 결 론

본 연구에서는 축계 비틀림진동 해석시에 고려되는 각종 감쇠들 중 프로펠러 감쇠 적용방법에 따른 해석 결과를 비교·검토하고, 특히 고효율 직결식 프로펠러가 적용된 선박의 경우 현 시점에서 사용상 적절한 프로펠러 감쇠방법을 제시하였다. 이를 요약하면 다음과 같다.

1) 추진축계 비틀림진동 해석에 적용되고 있는 많은 프로펠러 감쇠방법들을 비교·검토한 결과, 고효율 직결식 프로펠러를 장착하는 경우 해석치 대비 측정치가 30% 이상 낮은 결과를 주는 것을 알 수 있다. 따라서 고효율 프로펠러를 장착한 선박의 축계를 설계하고자 할 경우에는 프로펠러 감쇠계수를 기존 대비 20 ~ 30% 낮게 적용하는 방안이 적절하다. 하지만, 이는 이러한 프로펠러를 탑재한 추진축계에 따라 차이가 있을 수 있으므로 확인할 필요가 있다.

2) MDT New방법은 해석치가 측정치의 대비 10% ~ 20%정도 낮은 범위내에서 상당히 고르게 분포되고 있어 다른 방법들과 비교할 때 측정치에 가장 근접한 것을 확인하였다. 하지만 이 방법은 연료절약형 초장행정 엔진 (G type)을 탑재한 경우에는 그 경향이 상이할 뿐만 아니라, 프로펠러 형상을 고려하고 있지 않아 추후 프로펠러 형상의 변화에 따른 불확실한 오차가 발생할 가능성이 있어 향후 보다 물리적으로 타당한 프로펠러 감쇠 방법을 연구하여 적용할 필요가 있다.

3) 엔진 정격조정에 따른 프로펠러 감쇠특성의 변화를 검토한 결과 MDT New방법을 제외하고는 모든 방법들이 정격조정에 관계없이 감쇠계수가 동일한 것을 알 수 있었다. 그러므로 MDT New방법으로 프로펠러 감쇠를 적용하는 경우에는 공진점의 위치와 엔진 정격조정에 따라 계수를 달리 적용하는게 적절하다. 하지만 MDT New방법을 제외한 다른 방법을 적용할 경우에는 엔진 정격조정에 따라 해당 축계 설계에 반영되어 있으므로 사용 상 문제가 없을 것으로 판단된다.

References

• BICERA, Handbook of Torsional Vibration, Cambridge University Press, (1958).
• W. K. Wilson, Practical Solution of Torsional Vibration Problems, 1-5, Chapman & Hall, London, (1942).
• H. J. Jeon, and D. C. Lee, Vibration of Propulsion Shafting, Dasom publisher, (2003), (in Korean).
• Wartsila Switzerland Ltd, Propeller damping for torsional vibration calculation (DOC,11129), available at: http:/www. wartsila.com Accessed September 29, 2016.
• S. Schuster, On the influence of the propeller and the longitudinal and torsional vibrations in the waveguide, ship and port, 13, H. 6 p498, (1961), (in German).
• H. Schwankecke, Reflections on the hydrodynamic vibrations of the propeller and wall line, Yearbook, B. 57 p252-1963, (in German).
• Man Diesel & Turbo, Propeller damping for torsional vibration calculation of MAN B&W 2-stroke engines, available at: http://marine.man.eu Accessed September 21, 2016.
• Y. G. Kim, S, J. Hwang, J. S. Sun, S. G. Jung, and U. K. Kim, “A study on the effect of torsional vibration for propulsion shafting due to the characteristics of fuel saving marine engine”, Proceedings of the 39th KOSME Fall Conference, p186, (2015), (in Korean).
• Y. G. Kim, S. J. Hwang, Y. H. Kim, S. W. Kim, K. H. Cho, and U. K. Kim, “Control of torsional vibration for propulsion shafting with delayed engine acceleration by optimum design of a viscous-spring damper”, Journal of the Korean Society of Marine Engineering, 40(7), p580-586, (2016), (in Korean). [https://doi.org/10.5916/jkosme.2016.40.7.580]