TFT-LCD 셀 영상에서 주기적인 셀 패턴 제거 기반 결함검출

1. 서 론

TFT-LCD(Thin Film Transistor Liquid Crystal Display)는 고해상도, 저전력 소모 등의 장점을 바탕으로 디스플레이 장치로써 활용되고 있다[1]. TFT-LCD 산업의 발달과 함께 시장 경쟁의 심화로 관련 업체에서는 비용절감 및 성능 향상을 목표로 한다[2]. 이와 관련하여 영상처리를 이용한 TFT-LCD의 결함검출과 관련한 다양한 연구가 진행되고 있다[3]-[5]. TFT-LCD의 패널 구조 및 조명 특성은 제조사마다 상이하며, 결함 및 불량의 표준화의 어려움에 의해 최종 검사는 전문인력에 의존하고 있다. 하지만 이러한 전문인력에 의존한 검사의 경우 인력의 능력에 따라 검사 속도와 검사 결과가 상이할 문제가 있어 생산비 절감 및 품질 향상을 위해서는 신뢰성 있는 자동 결함 검사 시스템의 개발이 필수적이다. 이러한 자동 결함 검사 시스템의 개발은 카메라를 이용한 Vision 기반 검사 시스템의 연구가 일반적이며, 영상획득, 카메라 왜곡 보정 및 조명성분 제거 등의 전처리, 결함 후보 화소 검출, 결함 BLOB(Binary Largy OBject) 검출, 결함 BLOB 분석, 그리고 최종 결함 BLOB 검출과정 등으로 이루어진다. 이러한 Vision 기반 검사 시스템은 검사 대상의 특징에 따라 다양한 방법으로 진행된다. 그 중 TFT-LCD 셀 영상의 경우, 일반 TFT-LCD 영상과 달리 주기적인 셀 패턴을 포함하고 있는데, 셀 패턴의 휘도분포는 넓게 분포하며 특히, 결함의 휘도분포와 겹쳐 결함과 셀 패턴을 분리하기 어려운 문제가 존재한다. 이와 같은 경우 배경과 결함의 휘도분포가 서로 다른 특징에 기반하여 결함을 검출하는 TFT-LCD 결함검출 알고리즘[6]을 바로 적용하게 되면 셀 패턴이 결함으로 과검출 되는 문제가 발생한다. 따라서 TFT-LCD 셀 영상에 대해 신뢰성 있는 결함검출을 위해서는 셀 패턴 제거의 전처리 과정이 매우 중요하다.

주기적인 셀 패턴을 제거하는 대표적인 방법으로 피치 비교(Pitch Compare) 기법[7]을 이용한 셀 패턴 제거 방법이 있다. 이는 주기적인 셀 패턴을 갖는 영상에서 한 주기의 셀 패턴을 나타내는 피치 패턴을 기반하여 셀 패턴을 제거하는 방법이다. 그러나 영상 획득 과정에서 회전, 크기변화, 위치 이동 등의 기하학적 왜곡이 발생할 경우 셀 패턴 제거의 성능이 크게 저하되는 단점이 있다. 따라서 기하학적 왜곡이 발생할 경우에 신뢰성 있게 셀 패턴을 제거하는 방법이 필요하다.

본 논문에서는 획득된 영상 내에 회전 변화가 있는 경우에도 셀 패턴을 신뢰성 있게 제거하기 위하여 퓨리에 변환(Fourier Transform)[8]에 기반한 주기적인 셀 패턴 제거 방법을 제안한다. 제안 방법은 주어진 영상을 퓨리에 변환을 이용한 주파수 공간(Frequency Domain)으로 변환할 경우, 주기적으로 반복되는 셀 패턴은 주파수 스펙트럼으로 표현된 주파수 공간상에서 크기(Magnitude)가 큰 영역으로 나타나는 특징에 기반한다. 먼저, 주어진 셀 영상에 대해 퓨리에 변환을 이용하여 주파수 스펙트럼 영상을 구한다. 다음으로 스펙트럼 영상에 대해 적응적 필터를 이용하여 셀 패턴이 나타내는 스펙트럼 영역을 제거한다. 그리고 필터링 된 스펙트럼을 역퓨리에 변환을 이용하여 셀 패턴이 제거된 영상을 얻는다. 다음으로 셀 패턴이 제거된 영상에 대해 STD(Standard Deviation) 방법[6]을 적용하여 결함을 검출한다.

본 논문의 구성은 다음과 같다. 먼저 2장에서는 패턴 제거기법 및 결함검출기법에 대해 설명하고, 3장에서는 제안 방법을 적용한 실험결과를 통해 성능을 검증한다. 그리고 마지막으로 4장을 통해 결론을 맺는다.

2. 본 론

TFT-LCD 셀 영상의 가장 두드러진 특징은 영상 내에서 R,G,B 셀이 반복적으로 나타난다는 점이다. Figure 1은 이러한 TFT-LCD 셀 영상 중 하나의 예를 나타낸다. 셀 영상에서 R,G,B 패턴이 가지는 휘도 분포는 넓은 범위에 걸쳐있으며, 결함이 가지는 휘도와 유사할 수 있기 때문에 일반적인 저해상도 TFT-LCD 영상에서 결함을 검출하는 알고리즘을 적용하는 것은 많은 어려움이 있다. 따라서 결함검출에 있어 패턴 제거 과정 없이 결함을 검출하는 것보다 영상 내의 R,G,B 패턴의 유형과 특징을 분석하여 패턴을 견실히 제거함으로써 결함검출의 정확성을 높이는 것이 중요하다.

Figure 1:

Example of TFT-LCD cell image

2.1 피치 비교를 이용한 셀 패턴 제거

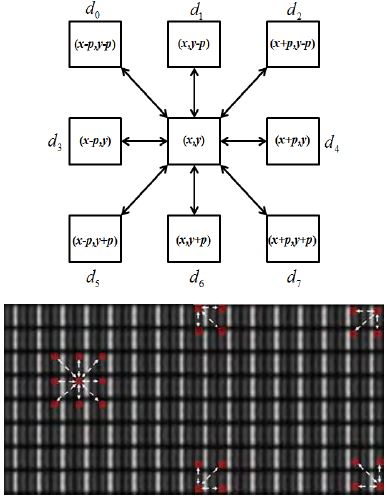
피치 비교(Pitch Compare) 방법은 TFT-LCD 셀 영상의 특징인 영상 내 특정 휘도 분포가 주기적으로 반복되는 점을 이용한다. 템플릿 영상(Template Image)을 사용하여 템플릿과 주어진 영상간의 비교를 통해 패턴을 제거한다. 여기서 패턴의 방향별 주기가 동일한 패턴을 피치 패턴(pitch parttern)이라 한다. 각 픽셀에 대해 Figure 2와 같이 화소간의 거리가 피치와 동일한 8방향 픽셀의 휘도를 비교한다.

Figure 2:

Mask and mask application scheme of pitch pattern compare method

Figure 3은 각 픽셀에 대해 Figure 2와 같은 8방향 피치 비교를 적용하였을 때 휘도값의 차를 나타낸 그림이다. 정상 영역은 8방향의 픽셀들과 동일한 휘도값을 가져 제거가 되었으며, 결함 영역은 결함의 종류에 따라 암결함 혹은 휘결함으로 표시가 된다.

Figure 3:

Pattern removal result using pitch pattern compare method

그러나 이러한 피치 비교 방법은 영상에 기울어짐이 존재하게 되면 피치 비교 방식이 적용이 어려우며 셀 패턴 제거가 난해할 뿐만 아니라 영상의 크기에 따라 수행시간이 크게 증가하는 문제점이 있다. Figure 4는 실제 TFT-LCD 셀 패턴 영상에 기울어짐 왜곡이 존재할 때 피치 비교방법을 적용한 결과로써, 결함의 유무를 판별하기 어려울 뿐만 아니라 피치의 방향과 기울어진 셀 패턴 간의 불일치로 영상 전체에 오검출이 발생함을 확인할 수 있다.

Figure 4:

The result of applying the pitch pattern compare method to distorted image

2.2 퓨리에 변환을 이용한 셀 패턴 제거

본 논문에서는 피치 비교 방식이 가지는 기울어짐 왜곡에 취약한 점과 영상의 크기가 커짐에 따라 수행시간이 크게 증가하는 문제를 해결하기 위해 퓨리에 변환을 이용한 주파수 영역에서의 셀 패턴 제거 방식을 제안한다.

TFT-LCD 셀 영상에 대해 퓨리에 변환(Fourier Transform)을 적용할 경우, 반복해서 나타나는 R,G,B 셀에 의해 높은 에너지를 가지는 스펙트럼 영역이 나타난다. 이러한 높은 에너지를 가지는 스펙트럼 영역을 제거한 후, 역 퓨리에 변환을 적용하게 되면 TFT-LCD 영상의 셀 영역이 제거된 영상을 획득할 수 있다.

먼저 f(x,y)는 TFT-LCD의 셀 영상을 나타내며, F(u,v)는 f(x,y)의 DFT(Discrete Fourier Transform)를 나타낸다. Figure 5는 전체 12000×1000 크기의 TFT-LCD 영상에 대해 결함이 포함된 영역을 1000×1000 크기로 잘라낸 영상과 해당 영상에 대해 결함이 포함된 부분을 100×100으로 잘라 확대한 그림이다.

Figure 5:

Example of defect in TFT-LCD cell image

1) 먼저 F(u,v)영상에 대해 스펙트럼의 크기 X(u,v)를 식 (1)과 같이 나타낸다.

$\[ X\left(u,v\right)=\left|F\left(u,v\right)\right| \]$

(1)

Figure 6은 Figure 5의 영상에 대한 스펙트럼 영상인 X(u,v)를 나타낸다.

Figure 6:

The spectrum image of Figure 5

Figure 6으로부터 스펙트럼 영상에서 0^o와 90^o 방향에서 큰 값을 가짐을 알 수 있고, 이들은 셀 패턴에 의해 스펙트럼이 크게 나타나게 된다.

2) 스펙트럼 영상 X(u,v)의 분포를 식 (2)와 같이 정규 분포 Z(u,v)로 변환한다.

$\[ Z\left(u,v\right)=\frac{X\left(u,v\right)-{\mu }_X}{{\sigma }_X} \]$

(2)

여기서 μ_X와 σ_X는 스펙트럼에서 계수들의 평균과 표준편차를 나타낸다. 일반적으로 셀 패턴의 주파수 계수는 스펙트럼의 평균 μ보다 큰 값을 가지므로 배경에 해당하는 스펙트럼의 계수는 작은 값을 가지며, 셀 패턴에 해당하는 스펙트럼의 계수일수록 큰 값을 가지게 된다.

3) Z(u,v)영상에 대해 Aliasing 오류를 줄이기 위해 Gaussian 마스크를 식 (3)과 같이 사용한다.

$\[ H\left(u,v\right)=Z\left(u,v\right)*G\left(u,v\right) \]$

(3)

여기서 G(u,v)는 Gaussian 마스크를 나타내고, * 연산은 Convolution 연산을 나타낸다.

필터 된 H(u,v) 영상에 대해 다음의 필터를 제안한다. 주파수 성분은 배경에 비해 상대적으로 높은 에너지를 가지므로 임계값 l을 사용하여 셀 패턴의 주파수 성분을 식 (4)과 같이 추출한다.

(4)

추출된 T(u,v) 스펙트럼 영상에 대해 식 (5)와 같이 초기 스펙트럼 영상 X(u,v)와 Convolution을 하여 셀 영역의 패턴을 제거한다.

$\[ R\left(u,v\right)=X\left(u,v\right)*T\left(u,v\right) \]$

(5)

Figure 7은 Figure 6의 영상에 대해 임계값 l = 2 일 때 필터 영상 R(u,v)를 나타낸다.

Figure 7:

The filtered image R(u,v) of Figure 6

4) R(u,v) 스펙트럼 영상에 대해 역 퓨리에 변환을 식 (6)와 같이 적용하여 셀 패턴이 제거된 영상 g(x,y) 를 얻는다.

$\[ g\left(x,y\right)=IDFT\left[R\left(u,v\right)\right] \]$

(6)

Figure 8은 Figure 5의 셀 패턴이 제거된 스펙트럼 영상에 대해 식 (3)을 적용하여 획득된 영상과 결함 부근 영역의 영상을 나타낸다. Figure 9는 Figure 5와 Figure 8의 결함 영역에 대한 라인프로파일을 나타낸 그림이다. Figure 9(c)와 같이 휘도는 규칙적으로 증가와 감소를 반복하며, 결함 영역에서 왜곡이 발생하는 형태임을 확인할 수 있다. 그리고 제안한 퓨리에 변환을 적용한 결과 셀 패턴영역이 제거되어 휘도가 크게 감소하고 결함 영역은 상대적으로 강조가 되어 남아있는 것을 확인할 수 있다.

Figure 8:

The cell pattern removal result image g(x,y)

Figure 9:

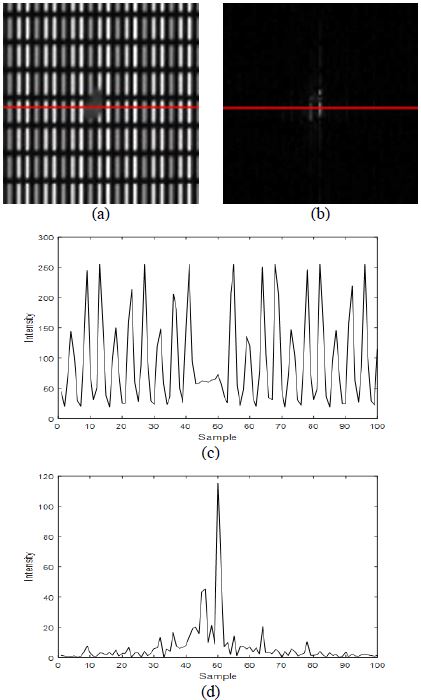
Line profile of cell pattern removal result. (a) cell pattern image, (b) cell pattern removal image, (c) line profile of (a), (d) line profile of (b)

5) Figure 10은 식 (4)에서 사용된 문턱값 l에 따른 셀 패턴이 제거된 영상 g(x,y) 와 결함 부근의 라인프로파일을 나타낸다. Figure 10(a)와 (b)로부터 l = 0과 l = 1 일 때는 셀 패턴이 제거가 되지만 결함에 왜곡이 발생하여 결함검출에 어려움이 있음을 확인할 수 있다. 또한 Figure 6(a)의 l = 2 일때와 Figure 10(c)의 l = 3 일 때의 경우에는 셀 패턴이 신뢰성 있게 제거되었으며, 결함이 잘 검출되었음을 확인할 수 있다. 그러나 Figure 10(d)로부터 l = 4 와 같이 임계값이 커질 경우 셀 패턴이 남아 있음을 확인할 수 있으며, 따라서 임계값은 약 2~3의 값일 때 적절한 셀 패턴 제거 및 결함 영역의 강조가 이루어짐을 알 수 있다.

Figure 10:

The cell pattern removal result image according to l, (a) l = 0, (b) l = 1, (c) l = 3, (d) l = 4

이와 같이 퓨리에 변환은 셀 패턴 제거에 효과적임을 확인할 수 있으며, 또한 영상의 기울어짐에도 강인한 특징을 갖고 있다.

다음 Figure 11은 퓨리에 변환이 영상의 기울어진 왜곡에도 강인함을 확인하기 위해 Figure 5의 영상에 대해 기울어짐을 적용하고 퓨리에 변환을 이용하여 셀 패턴을 제거한 영상이다.

Figure 11:

Removal of cell pattern using Fourier transform for slanted image

Figure 11에서 확인할 수 있듯이 퓨리에 변환은 영상의 기울어짐 왜곡에 다소 강인하여 셀 패턴 제거가 양호하게 되었음을 확인할 수 있다.

2.3 STD 방법을 이용한 결함검출

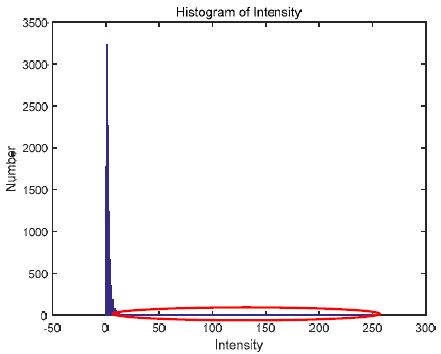
셀 패턴이 제거된 영상에서 결함 영역의 휘도는 배경 영역의 휘도에 비해 크거나 작은 차이를 나타내며, Figure 10(c)에 대한 히스토그램 영상인 Figure 12에서는 히스토그램의 대부분을 차지하는 평균으로부터 떨어진 붉은 원 영역의 화소들로 표현할 수 있다.

Figure 12:

Histogram of Figure 10 (c)

이는 영상의 평균과의 휘도차가 클수록 결함영역에 포함된 화소일 가능성이 높으며, 영상의 휘도평균과 표준편차를 이용하여 결함 화소들을 검출할 수 있음을 알 수 있다. 따라서 STD기반 결함검출 방법은 셀 패턴 영역이 제거된 영상 g(x,y)에서 식 (7)과 같이 임계값을 결정하여 결함화소를 검출한다.

$\[ \begin{array}{c}T{H}_H\left(k\right)={\mu }_g+k{\sigma }_g,\\ T{H}_L\left(k\right)={\mu }_g-k{\sigma }_g\end{array} \]$

(7)

여기서 μ_g과 σ_g는 영상 g(x,y)의 평균과 표준편차를 의미하며, k는 영상 g(x,y) 에서 결함이 차지하는 비율을 결정하는 가중치이다. Figure 13은 Figure 10(b)에 대해 STD 기반 방법에 의한 결함검출 결과 영상이다.

Figure 13:

Defect detection image using STD-based method for Figure 10 (b)(k = 4)

이와 같이 제안 방법은 STD 기반의 결함검출을 적용함으로써 배경영역의 휘도와 결함 영역의 휘도차에 따른 임계값을 결정하여 결함검출을 견실히 할 수 있다.

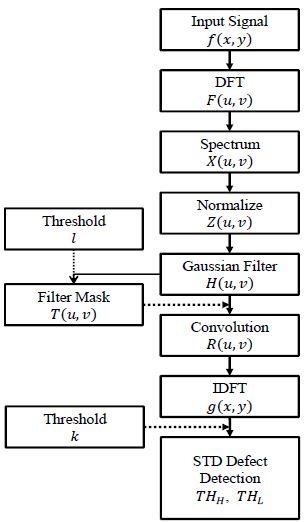
Figure 14는 제안한 TFT-LCD 셀 영상에서 셀 패턴 제거 기반 결함검출 알고리즘의 흐름도이다.

Figure 14:

Proposed algorithm flowchart

3. 실 험

실험영상은 결함을 포함한 실제 TFT-LCD 셀 영상에 대해 진행하였으며, 결함의 종류는 얼룩성 결함으로 실제 TFT-LCD 패널 생산 공정상에서 가장 빈번하게 발견되는 결함의 유형이다. 전체 TFT-LCD 영상의 크기는 12000×1000 사이즈의 영상이며, 본 논문에서는 400×400 크기의 결함이 포함된 영역에 대해 실험을 진행하였으며, 실험 결과는 결함 영역을 중심으로 100×100 크기의 영역에 대해 확대하여 나타내었다.

Figure 15는 제안 방법에 의해 실제 TFT-LCD 셀 영상의 패턴 제거 영상과 검출된 결함 영상을 나타낸다. 입력된 TFT-LCD 셀 영상인 Figure 15(a)에 대해 식 (5)와 같이 셀 영역의 스펙트럼을 제거한 후, Figure 15(b)와 같이 셀 영역을 제거한 영상을 획득한다. 그 후, Figure 15(c)와 같이 STD 방법을 적용하여 결함을 검출한다. Figure 15(a)의 입력영상과 Figure 15(c)의 결함검출 결과 영상의 비교를 통해 결함이 신뢰성 있게 검출되었음을 확인할 수 있다.

Figure 15:

A defect detection process applying the proposed algorithm. (a) cell image with defect. (b) image without pattern (c) STD defect detection results

Figure 16은 또 다른 결함 영상들에 대해서 동일한 알고리즘을 적용하여 결함을 검출한 결과이다. 제안 알고리즘을 적용한 결과 작은 크기나 작은 휘도차를 가지는 결함에 대해서도 신뢰성 있게 검출할 수 있었으며, 또한 400×400의 결함이 포함된 영역에 대해 결함검출까지 걸린 수행시간은 평균 0.03초로 매우 짧아 실시간 처리에도 적합함을 확인할 수 있었다.

Figure 16:

Comparison of defect detection results in cell images using proposed algorithm. (a)-(c) TFT-LCD cell Image with defect. (d)-(f) defect detection result image

4. 결 론

본 논문에서는 TFT-LCD 셀 패턴 영상에서 신뢰성 있는 패턴 제거에 기반한 결함검출 방법을 제안하였다. 제안 방법은 셀 패턴을 신뢰성 있게 제거하기 위하여 퓨리에 변환에 기반한 주기적인 셀 패턴 제거와 STD 방법에 의해 결함을 검출한다. 실험을 통해 제안 방법의 결함검출 성능이 우수함을 확인하였다. 특히 획득된 영상에서 기하학적 왜곡이 발생하면, 기존의 셀 패턴 제거 방법인 피치 비교 방법은 패턴 제거 성능이 저하되므로 신뢰 있게 결함을 검출하기 어려우나, 제안 방법은 패턴 제거 성능이 우수하므로 신뢰 있게 결함을 검출할 수 있다. 또한 400×400의 영상에 대해 평균 0.03초의 짧은 수행시간을 통해 실시간 결함검출에도 적합함을 확인할 수 있었다.

Acknowledgments

이 논문은 2016년도 정부(교육부)의 재원으로 한국연구재단의 지원을 받아 수행된 기초연구사업임(과제번호: 201616210000).

References

• J. Jang, S. K. Lim, and M. H. Oh, “Technology development and production of flat panel displays in Korea”, Proceedings of the IEEE, vol. 90(no. 4), p501-513, (2002).
• C. B. Moon, Y. H. Ahn, H. Y. Lee, B. M. Kim, and D. W. Oh, “Implementation of automatic detection system for CCFL’s defects based on combined lighting”, Journal of the Korea Industrial Systems Research, vol. 15(no. 2), p69-80, (2010), (in Korean).
• K. B. Lee, M. S. Ko, J. J. Lee, T. M. Koo, and K. H. Park, “Defect detection method for TFT-LCD panel based on saliency map model”, Proceedings of IEEE Region 10 Conference, p223-226, (2004).
• Y. H. Liu, S. H. Lin, Y. L. Hsueh, and M. J. Lee, “Automatic target defect identification for TFT-LCD array process inspection using kernel FCM-based fuzzy SVDD ensemble”, Expert Systems with Applications, vol. 36(no. 2), p1978-1998, (2009). [https://doi.org/10.1016/j.eswa.2007.12.015]
• S. L. Chen, and S. T. Chou, “TFT-LCD mura defect detection using wavelet and cosine transforms”, Journal of Advanced Mechanical Design, Systems, and Manufacturing, vol. 2(no. 3), p441-453, (2008). [https://doi.org/10.1299/jamdsm.2.441]
• W. S. Kim, D. M. Kwak, Y. C. Song, D. H. Choi, and K. H. Park, “Detection of spot-type defects on liquid crystal display modules”, Key Engineering Materials, vol. 270, p808-813, (2004).
• S. Uchikoga, and N. Ibaraki, “Low temperature poly-Si TFT-LCD by excimer laser anneal”, Thin Solid Films, vol. 383(no. 1), p19-24, (2001). [https://doi.org/10.1016/s0040-6090(00)01644-8]
• E. M. Stein, and G. Weiss, “Introduction to fourier analysis on euclidean spaces”, Princeton University Press, vol. 32, (2016).