[ Original Paper ]

Journal of the Korean Society of Marine Engineering - Vol. 41, No. 3, pp.222-229

ISSN: 2234-7925 (Print) 2234-8352 (Online)

Print publication date 31 Mar 2017

Received 13 Sep 2016 Revised 09 Feb 2017 Accepted 17 Mar 2017

DOI: https://doi.org/10.5916/jkosme.2017.41.3.222

탄-소성 손상모델을 활용한 고망간강의 인장거동 모사에 관한 연구

김종환¹ ; 이정호² ; 김슬기³ ; 전민성⁴ ; 이제명^†

Non-linear tensile behavior of high manganese steel based on elasto-plastic damage model

Jong-Hwan Kim¹ ; Jeong-Ho Lee² ; Seul-Kee Kim³ ; Min-Sung Chun⁴ ; Jae-Myung Lee^†

1Department of Naval Architecture and Ocean Engineering, Pusan National University, Tel: 051-510-2340 jonghwan@pusan.ac.kr
2Department of Naval Architecture and Ocean Engineering, Pusan National University, Tel: 051-510-2340 babopanda@pusan.ac.kr
3Department of Naval Architecture and Ocean Engineering, Pusan National University, Tel: 051-510-2340 meltcandy@pusan.ac.kr
4Central Research Institute, Samsung Heavy Industries, Tel: 042-865-4619 minsung.chun@samsung.com

Correspondence to: ^†Department of Naval Architecture and Ocean Engineering, Pusan National University, 2, Busandaehak-ro 63beon-gil, Geumjeong-gu, Busan 46241, Korea, E-mail: jaemlee@pusan.ac.kr, Tel: 051-510-2342

Copyright © The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

초록

고망간강은 저온환경에서 강도 및 내구성 측면에서 우수한 기계적 성질을 가지고 있다. 최근 고망간강은 우수한 강도와 내구성을 바탕으로 LNG 화물창내에서 사용되는 SUS강, 니켈강의 대체재로 고려되고 있다. 이러한 연구의 일환으로, 본 연구에서는 고망간강의 기계적 물성치와 비선형 거동을 조사하기 위해 상온/극저온(-110K)에서 인장시험을 수행하였다. 또한 재료의 거동을 모사하기 위해 수정된 탄-소성 손상모델을 ABAQUS가 제공하는 사용자지정 재료 서브루틴(UMAT)에 유한요소 정식화과정을 거쳐 탑재하였다. 마지막으로 UMAT을 적용한 유한요소해석을 수행하였고 제안된 UMAT의 유효성 검증을 위해 해석결과를 인장시험 결과와 비교하였다. 그 결과, 제안된 UMAT은 고망간강의 비선형 거동을 효과적으로 모사함을 확인하였다.

Abstract

High manganese steel exhibits excellent mechanical properties with respect to strength and durability at low temperatures. Recently, high manganese steel has been considered as an alternative to existing materials, such as nickel steeland SUS304L for application as tank material for Liquefied Natural Gas (LNG) cargo containment systems. In the present study, tensile tests were performed at room and cryogenic temperatures in order to investigate the mechanical properties and non-linear tensile behavior of high manganese steel. In addition, elasto-plastic damage model was applied using the finite element analysis software ABAQUS via a user defined material subroutine (UMAT) to describe the material behavior. Finally, the results of the finite element simulations using the UMAT were compared to those of the tensile tests in order to validate the proposed UMAT. It has been demonstrated that the UMAT can effectively describe the non-linear tensile behavior of high manganese steel.

Keywords:

고망간강, 탄-소성 손상모델, 유한요소해석, ABAQUS 사용자지정 재료 서브루틴(UMAT)

키워드:

High manganese steel, Elasto-plastic damage model, Finite element analysis, ABAQUS user defined material subroutine

1. 서 론

연속체역학 관점에서 재료의 거동을 표현하기 위해 손상과 관련된 구성모델을 개발 및 수정하는 연구는 끊임없이 수행되어왔다. 특히 손상에 대한 설명은 크게 현상학적 접근과 미시역학적 접근으로 나누어진다. 특히, 손상을 현상학적으로 설명하는 대표적인 손상모델은 Lemaitre 손상모델로 유효응력과 등가변형률 원리를 기반으로 하고 있다[1]. 해당 모델은 유한요소해석과 결합하여 재료내부의 손상과 파단을 예측하는데 널리 활용되고 있으며 많은 연구자들에 의해 수정된 모델이 제시되었다. 재료에 인장과 압축하중이 동시에 발생할 경우 압축하중에 의해 기공의 성장을 감소시켜는 효과(Crack closure effect)를 고려하여 수정된 모델이 개발되기도 하였다[2][3]. 또한 재료의 거동을 정교히 모사하기 위해 일부 재료에 대해서는 수정된 포텐셜 함수를 제안한 연구도 수행되었다[4][5]. De Souza [6]은 수치적 방법을 통해 구성방정식의 해를 구하는 과정을 하나의 비선형 방정식으로 간략화 하여 전산효율을 크게 향상시켰다. 이러한 연구들을 통해 연속체 손상역학 기반으로 한 손상모델이 효과적으로 재료의 거동을 모사할 수 있으며 신뢰할 수 있는 방법론임이 입증되었다.

한편 고망간강은 TWIP(TWinning Induced Plasticity) 강재로 충격에너지 흡수량이 높아 자동차, 건설 분야에서는 이미 널리 사용되고 있다. 이와 더불어 LNG 저장탱크 내의 강재로 활용되고 있는 SUS강, Nickel강을 대체할 수 있는 재료로 각광받고 있으며 극저온환경에서 높은 강도와 저렴한 가격이 장점이다[7]. 그러나 당장 적용되기에는 극저온환경에서의 거동과 관련된 연구가 부족한 실정이다.

실험을 통해 데이터베이스를 확보하는 것이 가장 이상적이지만 구조단위 이상의 실험이 필요할 경우 이를 구축하기 위한 시간과 비용이 만만치 않다. 이러한 이유에서 기본적인 물성을 확보한 뒤 유한요소해석을 통해 전산적인 평가를 수행하는 것이 일반적이다. 그러나 실험에서 획득한 데이터를 유한요소해석에 활용하기 위해서는 공칭응력-공칭변형률을 진응력-진변형률로 변환하는 과정이 필요하며 통상적인 변환식은 큰 변형률을 가지는 재료에 대해서는 정확도가 매우 낮다고 알려져 있다[8]. 그러므로 변환식을 활용한 데이터를 유한요소해석에 적용하는 것은 상대적으로 신뢰성이 떨어질 수밖에 없다. 이 문제를 해결하기 위해 정확한 진응력-진변형률 획득을 위한 연구들이 진행되고 있지만 시험편의 형상 및 재료에 따른 범용성이 떨어지고 획득한 데이터를 다시 유한요소해석에 적용해야하므로 번거로움이 있다. 이러한 상황에서 손상모델을 활용한 유한요소해석은 좋은 대안이 될 수 있다. 진응력-진변형률 데이터 없이 재료의 비선형 거동을 효과적으로 표현할 수 있으며 사용되는 재료상수와 경화함수에 따라 다양한 거동표현이 가능해 활용도가 크기 때문이다. 그 예로 SUS강의 경우는 Kim et al. [9]에 의해 점-소성 손상모델을 활용하여 노치를 가지는 재료의 인장거동을 전산적으로 모사한 연구가 수행되었다. 또한 LNG 단열시스템에 사용되는 Corrugated sheet의 인장거동을 구성방정식 모델을 통해 효과적으로 재료의 비선형 거동을 모사한 연구가 Kim et al. [10]에 의해 수행되었다. Nickel강 역시 손상모델을 적용한 유한요소해석을 통해 피로균열진전을 전산적으로 모사한 연구가 Kim et al. [11]에 의해 수행되었다.

이와 같은 방법으로 본 연구에서는 고망간강의 비선형거동을 효과적으로 모사하기 위해 탄-소성 손상모델을 활용한 유한요소해석을 수행하였다. 이를 위해 먼저 상온/극저온(110K) 인장시험을 수행하여 기계적 물성을 획득하고 비선형거동을 확인하였다. 이를 바탕으로 탄-소성 손상모델을 유한요소 정식화과정을 거쳐 상용프로그램 ABAQUS의 사용자지정 재료 서브루틴(UMAT)에 탑재하여 유한요소해석에 적용하였다. 유한요소해석의 경우, 인장시험을 모사하여 하중-변위 관계, 손상의 진전 등의 결과를 얻었다. 획득한 유한요소해석 결과는 실험결과와 비교하였고 개발된 UMAT이 효과적으로 고망간강의 비선형 거동을 모사함을 확인하였다.

2. 인장시험

이 장에서는 고망간강의 비선형 거동을 확인하고 물성을 획득하기 위해 해당 재료에 대한 인장시험 과정 및 결과를 정리하였다. 사용된 고망간강의 성분비는 아래의 Table 1에 나타내었다. 실험을 통해 얻어지는 기계적 물성은 이후 과정인 유한요소정식화 과정 및 해석에 적용되었다.

Table 1:

Chemical Composition of High manganese steel

2.1 실험장비 및 방법

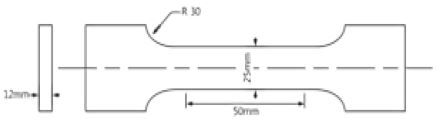
인장시험은 만능재료시험기(Universal Test Machine, UH1000KNI)를 이용하였으며 인장시험의 시험편 제작 및 방법은 KS B0801에 따라 진행하였다. 상온과 실제 LNG의 극저온환경을 고려한 설정온도 110K에서 실험을 수행하였다. 110K의 온도를 구현하기 위해 특수 제작된 극저온용 챔버 안에 액체질소를 분사하고 챔버 내부의 온도계 및 제어시스템을 통해 액체질소 분사량이 자동으로 조절되어 설정온도를 유지하도록 하였다. 극저온시험의 경우 시험편 내부의 열평형을 위해 1시간동안 예비 냉각작업을 수행하였다. 변위제어 방식으로 시험속도는 3mm/min로 설정하였으며 정확한 변형률 측정을 위해 극저온용 신율계(3542-050-100-LT, Epsilon)를 시험편 중앙부에 장착하여 인장시험을 수행하였다. 실험결과의 유효성 검증을 위해 각 조건에 따라 5회 반복실험 하였다. 위의 Figure 1은 극저온에서의 인장시험을 위한 극저온챔버를 탑재한 만능재료시험기와 신율계를 나타내며 Figure 2은 시험편의 치수를 도식적으로 보여준다.

Figure 1:

Experimental setup for tensile test of High manganese steel plate and extensometer

Figure 2:

Schematic diagram of tensile test specimen

2.2 인장시험 결과

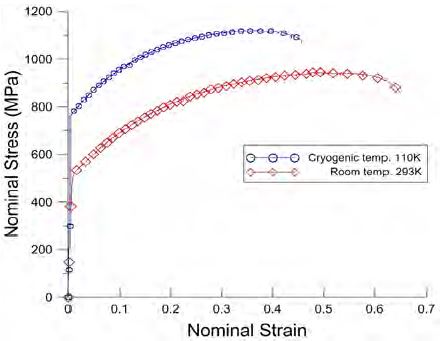
위의 Figure 3은 온도조건에 따른 고망간강의 인장시험 결과를 정리하여 대표적인 결과를 응력-변형률 그래프로 나타낸 것이다. 이 대표적인 결과는 5개의 실험결과 중 유사성이 가장 떨어지는 데이터 2개를 제거한 후 남은 3개의 데이터를 평균한 것이다.

Figure 3:

Representative results of tensile test for different temperature: 110K, 293K

먼저 상온 시험결과, 60%가 넘는 큰 연신율을 보이며 연성재료의 응력-변형률 그래프와 비슷한 경향을 보였다. 선형구간인 탄성영역에서는 일정한 기울기를 가지며 응력이 꾸준히 증가하다가 항복점 이 후 경화현상(Hardening)이 나타난다. 이는 TWIP강인 고망간강이 소성변형 중 오스테나이트(Austenite) 조직내에서 쌍정(Twinning)이 형성되면서 강도와 연신율이 크게 증가하기 때문이다. 또한 하중이 지속되면서 조직내에 ε-마르텐사이트(Martensite)의 분율이 점차 증가하게 되고 상변태에는 큰 에너지가 소모되기 때문에 경화현상이 지속된다. 그러나 마르텐사이트의 경우 강도증가에는 효과적이나 연성에는 악영향을 미친다. 따라서 고망간강의 경우 일반적인 연성재료와 달리 최대인장강도 이 후에 큰 변형률 없이 곧바로 파단에 이른다. 반면 110K의 극저온시험에서는 강도의 증가는 보였으나 연신율이 크게 줄어듦을 확인하였다. 이는 조직 내에서 ε-마르텐사이트와 α′-마르텐사이트로의 상변태가 빠르게 이뤄지면서 나타난 현상이다. α′-마르텐사이트 역시 강도적으로는 우수하나 연성에는 악영향을 미친다[12].

고망간강의 실험결과, SUS 및 Nickel 강의 비선형 거동과 유사하지만 최대인장강도 이후 급격히 파단되며 극저온에서는 연신율이 크게 줄어듦을 확인하였다. 따라서 강도가 높은 고망간강을 상기 재료의 대체재로 활용한다면 강도적으로 안정성을 꾀할 수는 있지만 허용변위 측면에서는 위험요소가 될 수 있다. 따라서 적용에 앞서 사용 환경에 따른 충분한 검토가 필요할 것이다.

3. 탄-소성 손상모델

3.1 Lemaitre 손상모델

Lemaitre 손상모델은 재료의 손상을 재료 내부 기공의 성장과 미소균열의 영향으로 인한 탄성계수 저하로 표현하고 내부 손상변수를 D로 정의하였다. 이를 일반적인 후크법칙(Hooke's law)로 나타내면 다음과 같다.

σ = 1 - D D : ε e

(1)

여기서, ε^e은 탄성변형률, D는 등방성 재료에 대한 강성텐서(Elasticity stiffness tensor)를 나타낸다. 손상 전의 초기 재료는 D=0의 값을 가지며 재료에 가해지는 하중이 지속될수록 점차 축적된다. 위 식의 응력텐서를 편차응력(Deviatoric stress)과 정수압응력(Hydrostatic stress)의 응력성분으로 나누면 다음과 같이 표현된다.

s= 1- D 2 G e e, p = 1 - D K v e

(2)

G와 K는 전단계수(Shear modulus)와 체적탄성계수(Bulk modulus)이며 e^e와 v^e는 각각 편차변형률텐서와 체적변형률을 나타낸다. 일반적으로 하중의 방향이 일정하다면 이동경화(Kinematic hardening)는 실질적인 효과를 보이지 않으므로 단순화된 Lemaitre 손상모델에서는 이를 무시한다. 이에 따른 von-Mises 기반의 항복함수는 다음과 같다.

Φ = q 1 - D - σ y R

(3)

q는 von-Mises 등가응력, R은 등방경화 내부변수(Isotropic hardening internal variable), σ_y은 등병경화 거동을 표현하는 경화함수이다. 또한 총 변형률은 탄성영역과 소성영역의 변형률합인 ε = ε^e + ε^p의 형태로 나타낼 수 있으며 그에 따른 증분형태는 다음과 같다.

ε ˙ = ε e ˙ + ε p ˙

(4)

이 때, 소성변형률 증분의 방향은 소성흐름법칙에 의해 항복함수의 접선방향에 항상 수직한 방향이다. 이를 표현하면 아래와 같다.

ε p ˙ = γ ˙ ∂ Φ ∂ σ

(5)

$γ ˙$ 은 소성승수(Plastic multiplier)이며 내부변수의 성장(Evolution)에 영향을 미치며 Lemaitre 손상모델에서 표현되는 손상의 진전에 관련된 식들은 앞서 언급한 Lemaitre [1]의 연구에 따라 아래와 같이 나타낼 수 있다.

ε ˙ = ε e ˙ + ε p ˙ R ˙ = γ ˙ D ˙ = γ ˙ 1 1 - D - Y r s Y = 1 2 1 - D 2 σ : D - 1 = - q 2 6 G 1 - D 2 - p 2 2 K 1 - D 2

(6)

Y은 손상에너지 해방률(Damage energy release rate)이며 r와 s는 손상의 진전과 관련된 재료상수이다. q와 p는 앞서 정의한대로 von-Mises 등가응력과 정수압응력을 각각 나타낸다.

3.2 탄-소성 손상모델의 유한요소 정식화

본 연구에서는 탄-소성 손상모델의 수치적 구현을 위해 Elastic predictor와 return mapping을 활용한 implicit기법을 채택하였다[13]. 아래는 유한요소 정식화과정의 주요 단계를 나타낸다.

Step 1: 변형률과 시도응력(Trial stress)을 아래와 같이 나타낸다. 초기에는 순수탄성영역으로 손상변수 D와 내부변수 R의 성장은 발생하지 않는다고 가정한다.

ε e trial = ε n e + Δ ε σ trial = 1 - D n D : ε e trial R trial = R n D trial = D n

(7)

D_n와 R_n은 각각 손상변수 D와 R의 증분형태로 n번째 항을 나타낸다.

Step 2: von-Mises 등가응력 q와 정수압응력 p을 계산하고 유효등가응력 $q ~$ 와 유효정수압응력 $p ~$ 을 아래와 같이 정의한다.

q trial = 32 s trial : s trial 1 / 2 q ~ trial = q trial 1 - D n p trial = 13 σ trial : I p ~ trial = q trial 1 - D n

(8)

Step 3: 항복함수 값을 계산하여 항복조건을 확인한다.

Φ t r i a l = q ~ trial - σ y R

(9)

만약 Φ^trial≤ 0을 만족한다면 응력상태는 탄성영역에 해당하므로 σ_n₊₁ = σ^trial이다. 다른 변수들도 (•)_n+1 = (•)^trial로 갱신되며 현재의 시간증분에 대한 수치계산을 종료한다. 반대로 Φ^trial> 0이라면 응력상태는 소성영역에 해당하므로 Step 4를 수행하게 된다.

Step 4: Return mapping을 통해 소성영역을 고려한 수정된 (•)_n+1의 계산과정이 수행된다.

ε n + 1 e + ε e trial - Δ γ 32 s n + 1 1 - D n + 1 s n + 1 R n + 1 = R n + Δ γ q n + 1 1 - D n + 1 - σ y R n + Δ γ = 0 q n + 1 = 1 - D n + 1 q ~ trial - 3 G Δ γ D n + 1 - D n - Δ γ 1 - D n + 1 - Y n + 1 r s = 0 - Y Δ γ, D n + 1 = 1 - D n + 1 q ~ trial - 3 G Δ γ 2 6 G 1 - D n + 1 2 + p ~ trial 2 2 K

(10)

Newton-raphson법을 이용하여 식 (10)의 세 번째와 다섯 번째 식을 만족하는 ∆_γ값을 얻는다.

Step 5: 계산된 ∆_γ을 바탕으로 Step 4의 변수들을 갱신한다.

Step 6: 현재 시간증분에 대한 수치계산을 종료한다. 새로운 시간증분에 대한 수치계산을 위해 위 과정이 반복적으로 수행된다.

4. 유한요소해석

앞서 언급된 손상모델에 대한 유한요소 정식화과정은 Fortran 언어로 코딩되어 상용 유한요소프로그램인 ABAQUS가 제공하는 UMAT(사용자지정 재료 서브루틴)에 탑재되어 사용자가 원하는 해당 재료만의 비선형특성을 유한요소해석에 반영시킬 수 있다. 또한 손상모델을 적용함으로써 일반적인 실험에서 획득할 수 있는 응력-변형률, 하중-변위 관계 외에 손상변수를 통해 재료의 손상을 정량적으로 확인할 수 있다는 장점이 있다.

4.1 기본 인장시험 시뮬레이션

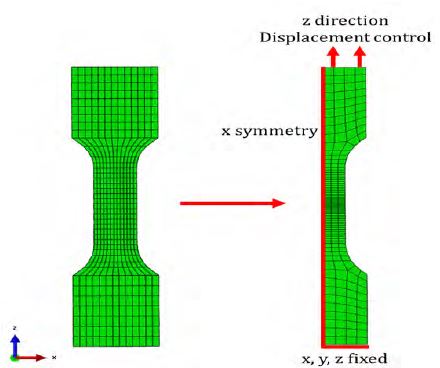
탑재된 UMAT에 대한 검증을 위해 재료단위 인장시험을 시뮬레이션 하였다. 먼저 실제 인장시험과 같은 경계조건을 적용하여 한쪽 끝은 고정시켜 움직임을 구속하였고 나머지 끝단은 변위제어를 통해 움직이도록 하였다. 또한 계산상의 효율성을 위해 인장시험편의 1/2 모델을 활용하였으며 이에 따른 대칭조건을 적용하였다. 사용된 요소는 3차원 8절점 감차적분요소(C3D8R)로 2148개의 요소 수에 3081의 절점 수를 가진다. 아래의 Figure 4은 유한요소 모델과 적용된 경계조건을 나타내었다.

Figure 4:

Finite element model of tensile specimen for ABAQUS UMAT

4.2 재료상수의 영향

선박재료상수 r와 s의 값을 결정하는 것은 손상역학 관점에서 매우 중요한 요소이며 논쟁을 초래할 수 있는 요소이다. 대부분의 값은 실험적으로 구해지며 연성재료의 경우 흔히 s = 1이 사용되고 r은 실험결과와의 비교를 통해 적절한 값으로 사용된다. 그러나 일부 연성재료에서는 s = 1 일 경우 실험결과와 일치하도록 거동을 표현하는 것이 불가능할 수 있다. 이러한 문제를 해결하기 위해 수정된 손상 포텐셜함수를 제안한 연구가 수행되기도 하였다. 그러나 기존에 작성된 유한요소 정식화과정을 대신하여 새로운 포텐셜함수에 맞게 정식화과정을 수정해야하므로 상당히 비효율적이다. 따라서 해당 재료의 거동만 확실히 표현할 수 있다면 s = 1 이외에 적절한 s 값을 사용하기도 한다[14][15].

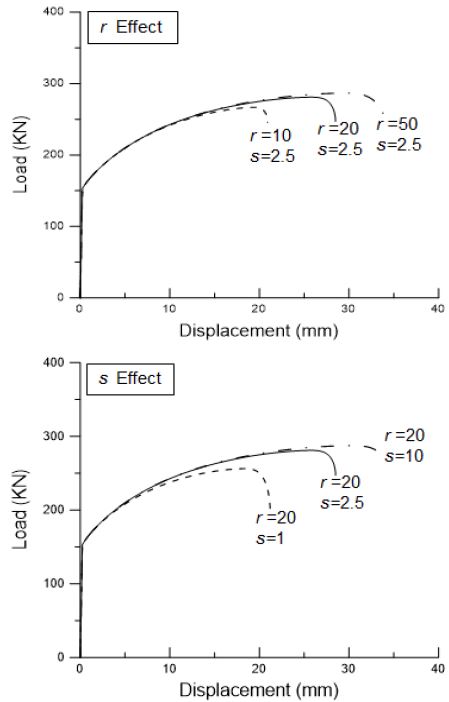
Figure 5은 재료상수에 따라 달라지는 인장시험 시뮬레이션 결과를 하중-변위 그래프로 나타낸 것이다. r과 s의 경우 전체적인 그래프의 경향에 영향을 미친다. 먼저 r의 경우 값이 증가하면서 하중-변위의 그래프의 형태는 유사하지만 미세한 하중의 증가와 변위증가를 확인할 수 있었다. 또한 r이 증가하면서 파단까지의 변위가 증가하여 이를 통해 변위 조정이 가능함을 확인하였다. 반면 s에 따라 재료의 거동이 크게 변화하였는데 특히 재료의 파단 근처에서 큰 효과를 보였다. s값이 감소할수록 급격한 하중저하를 보였다. 따라서 r와 s의 값을 적절히 조절하여 실험결과와 일치하는 시뮬레이션의 결과를 획득할 수 있을 것으로 판단하였다. 고망간강의 경우 상대적으로 r와 s 값이 높은 값으로 사용되어야만 이를 표현할 수 있었다.

Figure 5:

Graph of Load-displacement for FEA result according to damage parameter : r,s

그러나 r이 증가할수록 손상변수 D의 진전을 늦추지만 일단 성장하기 시작하면 급격하게 증가하게 된다. 이 때문에 0 ≤ D≤ 1로 정의된 손상 값이 수치계산 과정에서 D > 1 의 영역의 값을 가지면서 수렴성이 크게 떨어짐을 확인하였다.

4.3 수정된 Lemaitre 손상모델

앞서 손상의 진전과 관련된 재료상수인 r와 s이 재료의 거동에 미치는 영향을 확인하였다. 또한 유한요소해석의 결과가 고망간강의 거동을 효과적으로 표현할 수 있도록 r와 s의 값을 정하는 과정에서 문제점이 확인되었다. 따라서 손상의 진전을 늦추는 보정계수 k를 도입하여 수렴성을 높이도록 하였다. 또한 De Souza [6]에 의해 제안된 재료의 건전성을 나타내는 ω을 통해 구성방정식의 해를 구하는 과정을 하나의 비선형 방정식으로 간소화하는 과정을 활용하였다. 해당 모델은 알고리즘의 수렴성과 계산 효율을 크게 향상시킨다고 보고된 바 있다[16]. 이를 반영한 손상의 진전에 관한 지배방정식은 아래와 같다.

D ˙ = k Δ γ 1 - D - Y n + 1 r s

(11)

여기서 k는 0 ≤ k ≤ 1의 값으로 k = 1일 때 일반적인 Lemaitre 모델과 같다. 앞서 언급한 ω은 식 (10)을 치환하여 아래와 같이 표현할 수 있다.

ω ≡ 1 - D ≡ 3 G Δ γ q ~ trial - σ y R n + Δ γ ω n + 1 - ω n - k q ~ trial - σ y R n + Δ γ 3 G - Y Δ γ r s = 0

(12)

위의 식 (12)을 Newton-raphson법을 이용하여 이를 만족하는 Δ_γ값을 얻는다. 수치적 근사해를 얻기 위해 newton-raphson법을 적용할 때 초기 Δ_γ의 값을 0으로 정의하는 것이 일반적이지만 수렴성을 향상시키기 위해 Δ_γ⁽⁰⁾은 아래와 같이 정의된다.

Δ γ 0 = q ~ trial - σ y R n ω n 3 G

(13)

4.4 기본 인장시험 시뮬레이션 결과

Table 2은 인장시험 결과로부터 도출된 제안된 모델의 재료상수와 경화함수를 나타낸다. 상온에 비해 110K의 실험결과는 강도가 증가하고 연신율이 줄어듦으로 이를 반영하여 상온과 다른 항복강도, 재료상수가 적용되었다. 하지만 제시된 재료상수와 경화함수의 상수들은 고망간강의 비선형 거동을 표현할 수 있는 유일한 값이 아니므로 인장거동뿐만 아니라 압축, 전단, 비틀림 등의 다양한 실험을 통한 분석을 거친 후에야 비로소 유일한 변수 집합의 도출이 가능할 것이다.

Table 2:

Material data and Lemaitre damage model parameter for tensile test at each temperature

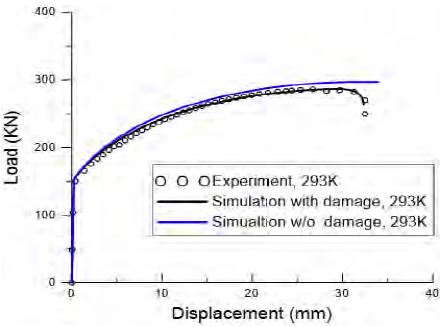
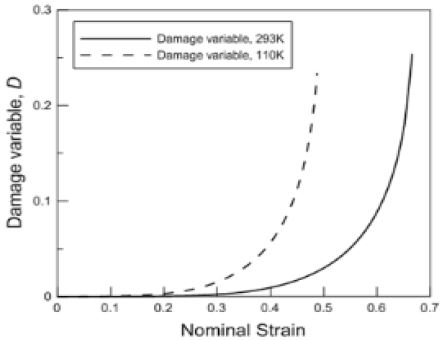
Figure 6은 상온 인장시험 시뮬레이션을 통해 획득한 수정된 Lemaitre 모델과 손상이 고려되지 않은 von-Mises의 모델의 결과를 실험결과와 비교하여 하중-변위 그래프로 나타낸 것이다. von-Mises 모델은 변위가 증가함에 따라 하중이 증가하는 형태를 보였으나 수정된 모델은 실험결과와 유사한 거동을 보이며 효과적으로 인장시험을 모사하였다. 또한 기존의 모델이 r이 증가하면서 초기에는 손상이 거의 발생하지 않다가 파단부에서 급격하게 손상이 증가하기 때문에 하중이 급격하게 떨어지고 수렴성이 좋지 못하였으나 수정모델에서는 k를 통해 손상의 진전을 지연시키면서 수렴성도 좋아지고 거동을 더욱 잘 표현할 수 있었다. Figure 7은 이에 통해 획득한 손상변수의 진전 양상을 나타낸다. 소성영역 초기까지는 거의 증가하지 않다가 최대 인장응력 이후부터 증가하기 시작하여 파단에 이른다.

Figure 6:

Representative result of experiment and simulation applied different damage model

Figure 7:

Growth of Damage variable D at each temperature : 293K, 110K

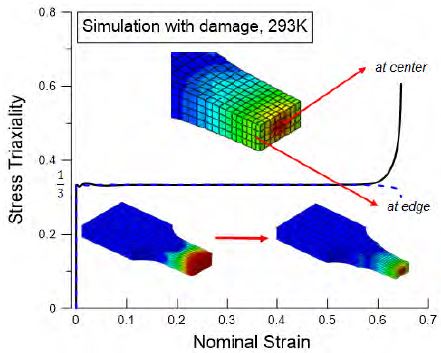
손상의 진전은 삼축응력비(Stress triaxiality)와 밀접한 관련이 있는데 이는 정수압응력과 von-Mises 등가응력의 비로 표현된다. 인장시험의 경우, 최대 인장응력 전까지는 단축응력이 지배적이지만 네킹(Necking)에 의해 단면적이 줄어들면서 다축응력이 발생하게 되고 삼축응력비가 증가하게 된다. 이는 손상의 진전을 유발하게 되고 결과적으로 재료를 파단에 이르게 한다[17].

Figure 8은 인장하중이 지속되는 동안의 손상변수의 변화양상 및 삼축응력비 값을 나타낸다. 초기 균일한 단축응력 상태에서는 손상변수가 시험편의 중앙과 가장자리에서 일정함을 알 수 있다. 그러나 네킹현상이 발생하고 다축응력상태로 변화하면서 손상변수의 최댓값이 내부로 점점 옮겨가는 것을 확인하였다. 이와 함께 삼축응력비의 값 또한 증가하였다. 따라서 해당 재료의 파단은 시험편의 중앙평행부 내의 가장 안쪽부터 파단이 진행되며 이후 바깥쪽 가장자리로 진전됨을 예측할 수 있었다.

Figure 8:

Contour of damage variable, D and graph of strain-stress triaxiality during tensile loading

4.5 구멍노치 인장시험 시뮬레이션 모델 및 결과

앞서 구멍(hole)은 가장 일반적인 노치형태로 엔지니어링 분야에서 다양한 목적으로 적용되고 있다. 그러나 구멍노치의 효과로 재료는 본래의 특성과는 다른 거동을 보인다. 따라서 제안된 모델의 유효성을 검증하기 위해 구멍노치를 가지는 인장시험편의 시뮬레이션을 추가적으로 진행하였다. 또한 이를 검증하기 위해 중앙평행부에 지름 8mm의 구멍노치를 가지는 시험편에 대한 상온/극저온에서의 인장시험을 수행하여 시뮬레이션과 비교하였다. 구멍노치를 가지는 인장시험 모델 역시 기본 인장시험과 마찬가지로 1/2모델을 활용하였고 경계조건 또한 동일하다. 사용된 요소는 3차원 8절점 감차적분요소(C3D8R)로 4432개의 요소와 5823개의 절점을 가진다.

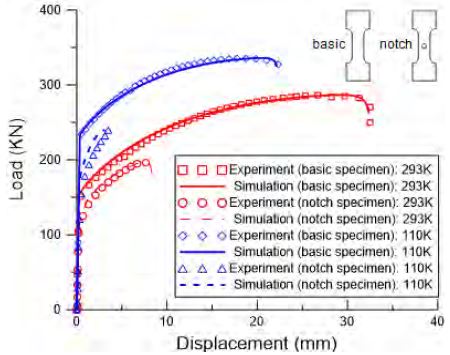
아래의 Figure 9은 제안된 모델을 활용한 상온/극저온, 기본인장시험/노치시험에 대한 시뮬레이션 결과와 실험결과를 비교하여 하중-변위 그래프로 나타낸 것이다. 극저온 노치시뮬레이션에 사용된 재료상수는 기본 인장시험 시뮬레이션과 동일한 값을 사용하였다. 이를 통해 제안된 모델을 적용한 UMAT이 효과적으로 고망간강의 기본/노치 인장거동을 효과적으로 모사함을 확인하였다.

Figure 9:

Comparison between experiment and simulation for basic/notch tensile test : 293K, 110K

5. 결 론

본 연구에서는 탄-소성 손상모델을 활용하여 고망간강의 비선형 거동을 유한요소해석을 통해 모사하였다. 이를 위해 고망간강의 인장시험을 수행하여 기계적 물성치를 획득하였다. 또한 탄-소성 손상모델이 유한요소 정식화과정을 거쳐 ABAQUS가 제공하는 사용자지정 재료 서브루틴(UMAT)에 탑재되어 유한요소해석에 활용되었다. 유한요소해석 결과는 인장시험 결과와 비교하여 그 유효성을 검증하였다. 본 논문의 연구 결과를 아래와 같이 요약한다.

(1) 극저온환경에서 활용가능성이 있는 고망간강에 대한 상온/극저온(110K)에서의 인장시험을 수행하였다. 그 결과 기존에 LNG 화물창 내에 사용되고 있는 SUS 강이나 Nickel에 비해 강도적으로 우수하며 경제성 측면에도 유리하여 극저온환경에서의 활용이 기대된다. 획득한 물성치와 재료상수는 유한요소 해석에 활용되었다.
(2) 수정된 탄-소성 손상모델은 Fortran 언어로 유한요소 정식화 과정을 통해 수치화하여 ABAQUS가 제공하는 사용자지정 재료 서브루틴에 탑재되어 유한요소해석에 활용하였다. 유한요소해석은 인장시험과 같은 조건으로 시뮬레이션 하였고 그 결과를 하중-변위 그래프로 도출하였다. 유한요소해석 결과는 인장시험 결과와 비교하였고 고망간강의 비선형 거동을 효과적으로 모사함을 확인하였다. 또한 구멍노치 인장시험을 추가적으로 수행하여 수정된 손상모델의 유효성을 검증하였습니다.
(3) 본 연구에서는 고망간강의 인장거동에만 초점을 맞추어 진행하였으나 균열진전이나 구조단위의 거동 등을 전산적으로 평가할 수 있는 모델이 개발되기 위해서는 압축, 전단, 비틀림 등의 시험이 추가적으로 수행되어야한다.

Acknowledgments

이 논문은 2015년도 정부(미래창조과학부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(No. 2015R1A2A1A15052688). 이 논문은 2013년도 정부(미래창조과학부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(No. 2011-0030013).

References

J. Lemaitre, “A continuous damage mechanics model for ductile fracture”, Journal of Engineering Materials and Technology, vol. 107(no. 1), p83-89, (1985). [https://doi.org/10.1115/1.3225775]
P. O. Bouchard, L. Bourgeon, S. Fayolle, and K. Mocellin, “An enhanced Lemaitre model formulation for materials processing damage computation”, International Journal of Material Forming, vol. 4(no. 3), p299-315, (2011). [https://doi.org/10.1007/s12289-010-0996-5]
D. Kujawski, “Enhanced model of partial crack closure for correlation of R-ratio effects in aluminum alloys”, International Journal of Fatigue, vol. 23(no. 2), p95-102, (2011). [https://doi.org/10.1016/s0142-1123(00)00085-2]
W. H. Tai, and B. X. Yang, “A new microvoid-damage model for ductile fracture”, Engineering Fracture Mechanics, vol. 25(no. 3), p377-384, (1986).
S. Chandrakanth, and P. C. Pandey, “An isotropic damage model for ductile material”, Engineering Fracture Mechanics, vol. 50(no. 4), p457-465, (1995). [https://doi.org/10.1016/0013-7944(94)00214-3]
E. A. De Souza neto, “A fast, one‐equation integration algorithm for the Lemaitre ductile damage model”, Communications in Numerical Methods in Engineering, vol. 18(no. 8), p541-554, (2002). [https://doi.org/10.1002/cnm.511]
J. S. Lee, K. S. Kim, Y. I. Kim, C. H. Yu, J. I. Park, and B. H. Kang, “Fatigue strength assessment of high manganese steel for LNG CCS”, Journal for the Society of Naval Architects of Korea, vol. 51(no. 3), p246-253, (2014). [https://doi.org/10.3744/snak.2014.51.3.246]
K. Y. Lee, T. H. Kim, and H. I. Lee, “Acquirement of True Stress-strain Curve Using True Fracture Strain Obtained by Tensile Test and Fe Analysis”, The Korean Society of Mechanical Engineers A, vol. 33(no. 10), p1054-1064, (2009). [https://doi.org/10.3795/ksme-a.2009.33.10.1054]
S. K. Kim, C. S. Lee, J. H. Kim, M. H. Kim, and J. M. Lee, “Computational evaluation of resistance of fracture capacity for SUS304L of liquefied natural gas insulation system under cryogenic temperatures using ABAQUS user-defined material subroutine”, Materials & Design, vol. 50, p522-532, (2013). [https://doi.org/10.1016/j.matdes.2013.03.064]
S. K. Kim, J. H. Kim, M. H. Kim, and J. M. Lee, “Numerical model to predict deformation of corrugated austenitic stainless steel sheet under cryogenic temperatures for design of liquefied natural gas insulation system”, Materials & Design, vol. 57, p26-39, (2014). [https://doi.org/10.1016/j.matdes.2013.12.037]
S. K. Kim, C. S. Lee, J. H. Kim, M. H. Kim, B. J. Noh, and J. M. Lee, “Estimation of fatigue crack growth rate for 7% nickel steel under room and cryogenic temperatures using damage-coupled finite element analysis”, Materials, vol. 5(no. 2), p603-627, (2015). [https://doi.org/10.3390/met5020603]
S. S. Sohn, S. M. Hong, J. H. Lee, B. C. Suh, S. K. Kim, and B. J. Lee, “Effects of Mn and Al contents on cryogenic-temperature tensile and Charpy impact properties in four austenitic high-Mn steels”, Acta Materialia, vol. 100, p39-52, (2015). [https://doi.org/10.1016/j.actamat.2015.08.027]
N. Aravas, “One the numerical integration of a class of pressure-dependent plasticity”, International Journal for Numerical Methods in Engineering, vol. 24(no. 7), p1395-1416, (1987).
K. Jin, X. Guo, J. Tao, H. Wang, N. Kim, and Y. Gu, “A model of one-surface cyclic plasticity with Lemaitre damage criterion for plastic instability prediction in the incremental forming process”, International Journal of Mechanical Sciences, vol. 114, p88-97, (2016). [https://doi.org/10.1016/j.ijmecsci.2016.05.016]
P. Hu, D. Shi, L. Ying, G. Shen, and W. Liu, “The finite element analysis of ductile damage during hot stamping of 22MnB5 steel”, Materials & Design, vol. 69, p141-152, (2015). [https://doi.org/10.1016/j.matdes.2014.12.044]
M. Mashayekhi, S. Ziaei-Rad, J. Parvizian, J. Nikbin, and H. Hadavinia, “Numerical analysis of damage evolution in ductile solids”, Structural Integrity & Durability, vol. 1(no. 1), p67-82, (2005).
D. Anderson, S. Winkler, A. Bardelcik, and M. J. Worswick, “Influence of stress triaxiality and strain rate on the failure behavior of a dual-phase DP780 steel”, Materials & Design, vol. 60, p198-207, (2014). [https://doi.org/10.1016/j.matdes.2014.03.073]

Element(wt.%)
C	0.3682	S	0.0016
Si	0.184	Cr	3.073
Mn	23.704	Cu	0.511
P	0.0205	Sol-Al	0.044

Parameter	293K	110K
Young's modulus, E	175 GPa	175 GPa
Poisson's ratio, v	0.3	0.3
Yield stress, σ_y₀	520 MPa	780 MPa
Damage parameter, s	4.7	8.3
Damage parameter, r	20 MPa	15.2 MPa
Correction factor, k	0.76	0.81