다수 풍력터빈의 후류영향 최소화 및 연간발전량 극대화를 위한 부유식 파력-해상풍력 플랫폼 최적배치

1. 서 론

풍력터빈 후류는 거리에 따라 근거리후류(near-wake)와 원거리후류(far-wake)로 구분된다[1]. 근거리후류는 로터 후방으로 약 1.0D ~ 2.5D(D: rotor diameter)로 발달하며, 이 영역에서는 후류풍속 저감 율이 주로 풍력터빈의 구조적형상에 의해 결정된다. 후류영역에서의 풍속감소율은 로터회전면을 통과한 바람에너지의 변환과정에서 발생하는 압력차에 따라 결정되는데, 로터후방으로 후류가 발달함에 따라 압력은 서서히 회복되고 풍속은 감소하게 된다.

Schepers et al. [2]은 ENDOW 프로젝트를 통해 수행된 여러 실험과 문헌조사를 통해 전단 층이 후류중심에 이르는 원거리후류의 시작점이 로터후방 2.25D 이후라고 제시한바 있다. 일반적으로는 로터후방 2.5D 단면을 기준으로 그 이상의 영역에서 발달하는 후류를 원거리후류라 하며 단면에서의 속도분포는 포물선 형태를 보인다. 육·해상 풍력단지는 제한된 부지면적 내에서 연간발전량 극대화를 위해 다수 풍력터빈의 최적배치설계를 실시하는데, 이때 전・후방터빈들의 상호 후류영향 최소화를 위해 최소 2.5D 이상의 이격거리를 유지한다. 특히 전방터빈 근접후류영역에서의 고 난류강도 및 높은 풍속감소율은 후방터빈의 에너지생산량 및 피로수명 감소에 매우 큰 영향을 미치기 때문에 대부분의 육・해상풍력단지에서 2.5D 이하의 이격거리를 갖는 터빈배치는 찾아볼 수 없다.

유럽연합(EU)의 지원으로 수행된 Upwind 프로젝트[3]에서는 덴마크의 Horns Rev 해상풍력단지를 대상으로 풍력터빈배열(7.0D)에 따른 출력 비를 측정하였다. 이후, 다양한 엔지니어링 후류모델과 CFD에 근거한 단지설계 소프트웨어들의 후류손실 예측정확도 평가를 실시하였고, CFD를 제외한 대부분의 엔지니어링 후류모델들이 후류손실을 과소 예측하는 경향을 보인다는 연구결과를 제시한바 있다[4].

Choi et al. [5]은 풍력터빈 이격거리변화(3D ~ 7D)가 후방터빈 출력감소에 미치는 영향을 분석하기 위해 정격풍속조건에서 정상상태 CFD 해석을 수행하였으며, 이격거리가 클수록 후류풍속이 빠르게 회복되어 출력감소율이 낮아진다고 보고하였다. 현재까지 발표된 연구결과들은 대부분 원거리영역에서의 후류가 출력성능에 미치는 영향에 한해 다루고 있으며, 근거리 후류영역에 위치한 후방터빈의 출력 및 연간발전량변화에 관한 선행연구들은 찾아볼 수 없는 실정이다.

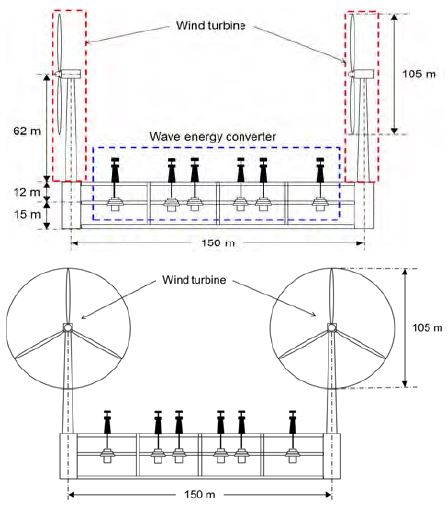
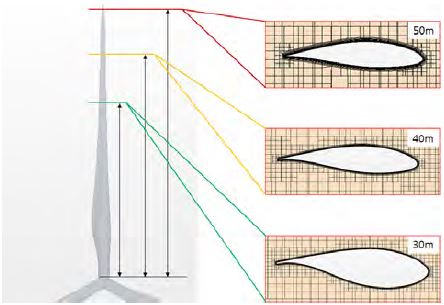
우리나라에서는 최근 선박해양플랜트연구소(KRISO)가 10MW급 부유식 파력-해상풍력 연계형 복합발전시스템 개발을 위한 설계연구를 수행한 바 있으며, Figure 1에 나타낸 바와 같이 정사각형(폭 150m) 부유체를 공유하여 풍력터빈 4기와 파력발전장치 24기가 설치된다.

Figure 1:

Conceptual configuration of the floating wave-wind hybrid power generation system(KRISO)

풍력터빈의 로터직경과 블레이드 길이는 각각 105m와 51m로 11.7m/s 조건에서 3MW의 정격출력을 발생시킨다. 풍력터빈 이격 거리는 주 풍향 변화에 따라 최대 약 2D (212m)에 이르게 되며 이격 거리 변화에 따라 후방 풍력터빈에 작용하는 근접후류의 영향이 다르게 나타나게 된다.그러나 풍력터빈 후류손실예측에 적용되고 있는 다양한 엔지니어링 후류모델들은 근거리후류영역에서의 후류손실을 예측하지 못하는 문제점이 있다. 따라서 신뢰성 있는 근접후류영향평가를 위해서는 full-scale 모델링된 풍력터빈형상을 이용하여 시간변화에 따른 전산유체해석(transient CFD analysis)을 수행 할 필요가 있다.

본 연구에서는 KRISO에서 설계된 부유식 복합발전단지 플랫폼 최적배치를 위해 총 4기의 풍력터빈 로터형상을 모델링하여 비정상 CFD 해석을 수행하였고, 근접후류영향을 받는 풍력터빈들의 연간에너지발전량감소율을 분석・제시하였다. 또한 상업풍력단지에서 측정된 데이터와의 비교를 통해 CFD 시뮬레이션 결과의 타당성을 확인하였다.

2. 풍력터빈 배치 및 해석조건 정의

2.1 부유식 플랫폼 배치각도

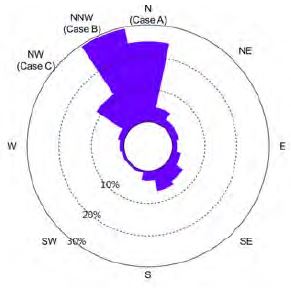
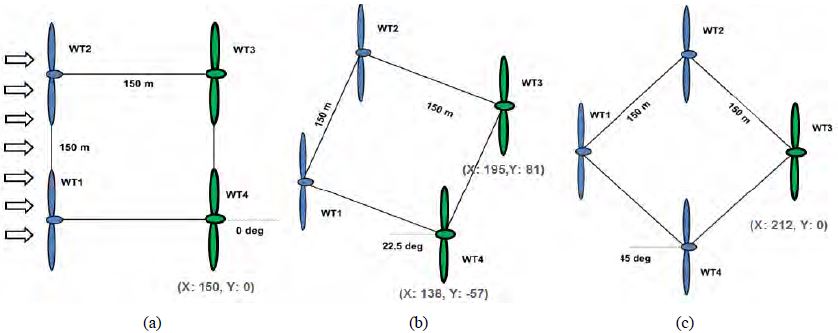
에너지장미(energy rose)는 풍력터빈 설치지역에서의 풍향별 연간에너지밀도를 나타내며 주풍향 결정에 중요한 척도로 활용된다. Figure 2는 부유식 플랫폼 설치 후보지인 제주도 서쪽 해상(126.12E, 33.30N) 근방에서 측정된 에너지장미이며, NNW(30%), N(24%), NW(12%) 방향으로 뚜렷한 분포를 보이고 주풍향은 NNW이다. Figure 3은 주풍향에 대한 부유식 플랫폼 설치조건을 나타내며, 각도변화에 따라 Case-A(0°), Case-B(22.5°)와 Case-C(45°)로 구분하였다. 바람 진행방향으로 가장 전방에 위치한 풍력터빈이 WT1이고 시계방향으로 각각 WT2, WT3, WT4로 정의하였다.

Figure 2:

Energy rose distribution at a proposed site

Figure 3:

Arrangement of floating platforms according to the variation of wind direction(a: Case-A, b: Case-B, c: Case-C)

2.2 다수 풍력터빈 해석조건

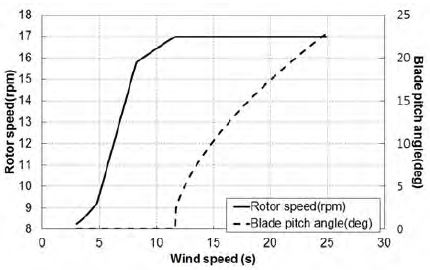
유입풍속변화에 따른 3MW 풍력터빈의 로터속도와 블레이드 피치각도 정보는 풍력터빈시스템 공-탄성시뮬레이션(aero-elastic simulation) 도구인 BLADED를 이용하여 계산되었다. Figure 4는 BLADED를 이용하여 계산된 3MW급 가변 속도형 풍력터빈의 풍속별 로터속도 및 블레이드 피치각도 변화를 나타낸다. 정격풍속(11.7m/s) 이하의 구간에서는 피치각도 변화가 없고, 발전기 측 토크제어의 영향으로 17rpm까지 로터속도가 증가한다. 정격풍속 이후의 구간에서는 출력제어를 위해 피치각도가 22.89°까지 증가하기 때문에 로터속도가 종단풍속(25m/s)까지 일정하게 유지되고 있다. CFD 해석에 필요한 풍속 별 로터회전속도 및 블레이드 피치각도 정보를 Table 1에 나타내었다.

Figure 4:

Calculation result on the rotor speed and the blade pitch angle as a variation of inflow wind speed

Table 1:

Rotor speed and blade pitch angle variation of up-stream wind turbines

Figure 3에서 후방에 위치한 풍력터빈의 로터회전속도와 피치각도는 후류영향으로 인해 감소된 유입풍속의 영향으로 Table 1에 나타낸 값과 다르게 나타난다. 따라서 본 연구에서는 더욱 현실적인 외부환경조건의 적용을 위해 단일 풍력터빈을 이용한 CFD 해석을 수행하였으며, Figure 3에 초록색으로 표현된 WT3 또는 WT4의 로터회전면 좌표지점에서의 평균 풍속 값을 획득하였다. 이상과 같은 단일 풍력터빈 해석결과를 이용하여 Figure 4로부터 후방 풍력터빈들의 로터회전속도와 피치각도 값을 얻었으며, Case-A(WT3, WT4), Case-B(WT3, WT4), Case-C(WT3)에 적용하여 다수풍력터빈 배치에 따른 비정상 상태 CFD 해석을 수행하였다.

3. 수치해석 조건

단일 풍력터빈 및 다수 풍력터빈에 대한 CFD 해석을 위해 STAR-CCM+ v10.04를 사용하였다. 대다수의 CFD 코드에서 기본 난류모델로 선택하고 있는 standard k-ϵ 모델의 경우, 실속지연, 박리지점 및 와류발생 크기 예측실패 등의 원인으로 특히 실속 후 영역에 대한 공력성능의 예측정확도가 낮으며, 풍력터빈 블레이드에 작용하는 토크 값을 과도하게 예측하는 결과를 보인다는 연구결과가 발표된 바 있다[6]-[9]. 서 본 연구에서는 특히 유체기계분야에서 강한 역 압력구배에 의한 유동박리의 예측성이 우수한 것으로 잘 알려진 Menter[10]의 SST k-ω 모델을 적용하였다.

단일 및 다수 풍력터빈의 계산격자 생성을 위해 trimmed mesh를 사용하였으며 각각 약 1.9×10⁷ cell과 8.1×10⁷ cell의 격자점을 생성하였다. 격자생성과정에서 모든 벽면으로부터 첫 번째 격자점을 점성저층영역에 위치시켰으며(y+<1) 경계층영역의 충분한 공간해상도 확보를 위해 약 10개의 프리즘격자를 배치하였다. 생성된 블레이드 반경방향 단면 대표격자의 형태를 Figure 5에 나타내었다.

Figure 5:

Computational mesh at the blade sections

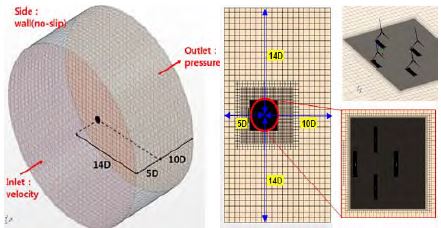
단일 및 다수 풍력터빈의 해석도메인은 로터중심으로부터 입구경계면까지 로터직경의 5배, 출구경계면까지 10배, 반경방향으로 14배의 거리를 확보하였으며, Figure 6에 나타내었다. 입구경계조건으로써 10%의 난류강도를 갖는 균일한 유입풍속을 적용하였고, 출구경계조건은 대기압 출구조건, 반경방향 경계면에 노슬립(no-slip)조건을 부여하였다. 로터도메인의 회전경계조건으로써 MRF(Moving Reference Frame)와 SMM(Sliding Moving Mesh)기법을 적용하였다. SMM 기법을 이용할 경우 정확한 후류유동해석이 가능하지만, 오랜 수렴시간이 필요하기 때문에 MRF 기법을 적용한 정상상태 유동해석을 통해 충분히 안정화된 유동장 정보를 초기조건으로 사용하였다[11]. 비정상상태 유동해석은 총 115s 동안 진행되었으며, 최종 시간간격은 0.025s 이다.

Figure 6:

Definition of boundary condition and computational domains(Left: single WTG, Right: multiple WTGs)

RMS 잔차를 기준으로 10^-3 이하의 조건을 1차적인 수렴판정기준으로 하였고, 목표 유동변수(추력, 토크) 값의 변화를 확인하여 반복계산 과정에서 모니터링 중인 유동변수 값의 변화가 없거나 특정 값을 기준으로 주기적인 변화를 보이는 경우에 한해 해가 완전히 수렴되었다고 판단하였다.

4. 결과 및 고찰

4.1 단일 풍력터빈 운전조건 및 유동해석결과

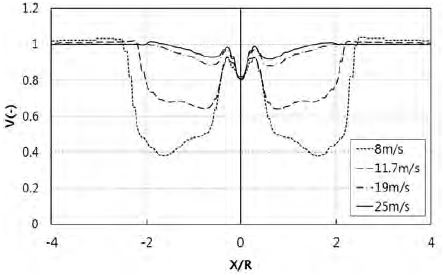
다수 풍력터빈조건에서의 유동해석에 필요한 후방터빈의 운전조건을 결정하기 위해 단일 풍력터빈 유동해석을 선행하였다. 유동해석 결과로부터 조건 별(Case-A, B, C) 후류거리 및 로터가 차지하는 면적에 대한 평균풍속을 구하였으며, Figure 4의 운전정보를 이용하여 로터회전속도와 피치각도를 계산하였다. 단일풍력터빈 유동해석을 통해 정의된 후방터빈 운전조건정보(회전속도 및 피치각도)를 Table 2에 나타내었다. Figure 7에 나타낸 바와 같이, 모든 풍속조건에서 유입풍속이 감소할수록 후류영역에서의 풍속 감소율이 증가하는 경향을 보였으며, 특히 8m/s 조건에서 Case-A와 Case-C의 풍속 감소율은 최대 약 60%에 이르는 것으로 확인되었다.

Table 2:

Wind speed deficit and operational conditions of the down-stream wind turbines

Figure 7:

Wake patterns of a single wind turbine for wind speed variation(2.0D)

Case-B의 경우, 후방터빈(WT3) 로터면적의 약 50% 만이 전방터빈의 후류영향을 받기 때문에 상대적으로 낮은 풍속 감소율(약 25%)를 보이며, 정격풍속 이후의 조건에서는 풍속감소가 발생하지 않았다.

4.2 다수 풍력터빈 출력특성 분석 및 검증

4.2.1 출력손실 분석결과

전술한 바와 같이, 단일터빈 유동해석을 통해 결정된 후방터빈의 풍속 및 운전조건을 적용하여, 다수 풍력터빈이 설치된 플랫폼 배치조건변화(Figure 2)에 따른 유동해석을 수행하였다. WT1은 모든 조건에서 후류영향을 전혀 받지 않기 때문에 이를 기준으로 Table 3에 개별 풍력터빈들(WT2 ~ WT4)의 상대적 출력비 해석결과를 나타내었다.

Table 3:

Power ratio variation of down-stream wind turbines

Figure 8은 플랫폼 배치조건변화에 따른 유입풍속 8m/s 에서의 허브 높이 단면 속도분포결과이다. 주 풍향에 대해 직사각형 배치를 갖는 Case-A 플랫폼 조건에서 WT1과 WT2는 후류영향을 받지 않는 반면, WT3, WT4의 로터면적은 전방터빈(WT1, WT2)의 후류영역에 완전히 포함된다. A-1(8m/s)과 A-2(11.7m/s) 조건의 경우, 후방터빈 출력이 후류영향에 의해 최대 약 90%, 60% 수준으로 감소되는 반면, A-3(19m/s)와 A-4(25m/s) 조건에서는 약 5% ~ 15% 수준의 출력손실이 발생하는 것으로 나타났다.

Figure 8:

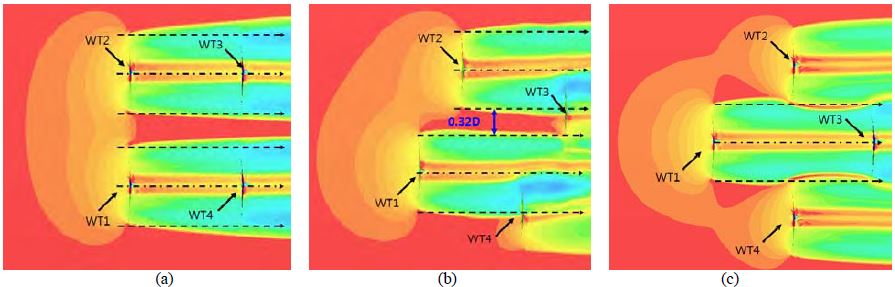
Velocity contour fields at hub height of the floating platforms (a: Case-A, b: Case-B, c: Case-C, 8m/s)

시계방향으로 22.5° 회전된 Case-B 플랫폼의 경우, WT2는 WT1의 영향으로 유입풍속조건변화에 따라 0.8 ~ 7.3% 수준의 출력상승효과를 보인다. Case-B의 후방터빈들은 Case-A에 비해 상대적으로 후류영향을 덜 받기 때문에 후방터빈의 출력감소율이 최대 3.3% ~ 45.2% 수준으로 나타났으며, 동일조건에서의 Case-A 플랫폼 배치에 비해 발전량 측면에서 우수한 것으로 판단된다. 다만, 불 균일 풍속조건에 노출된 로터에 작용하는 부가적 주기하중의 영향으로 피로수명 감소에 대한 우려가 있다.

45° 각도로 회전된 Case-C 플랫폼의 경우, WT1, WT2, WT4는 후류영향에 노출되지 않으며 WT3만 WT1의 후류영역에 완전히 포함된다. 최전방터빈(WT1)의 영향으로 인해 Case B-WT2의 경우와 마찬가지로 WT2, WT4의 출력이 일부 증가하는 효과가 나타나고 있으며, 전체 로터면적이 후류영향을 받는 WT3의 출력은 Case-A와 유사한 수준(4.5% ~ 85.7%)으로 감소하는 경향을 보인다.

유입풍속이 증가할수록 전방터빈 후류영역의 속도 감소율이 낮아지기 때문에(Figure 7) 후방터빈들의 출력감소율이 크게 개선되고 있으나, 저 풍속영역에서는 최대 출력감소율이 89.4%에 이르고 있다. 따라서 Case A-WT3, WT4, Case C-WT3과 같이 로터면적의 100%가 후류영역에 포함되는 풍력터빈 배치는 반드시 피해야 할 것으로 판단된다.

4.2.2 유사조건 실측데이터와의 비교결과

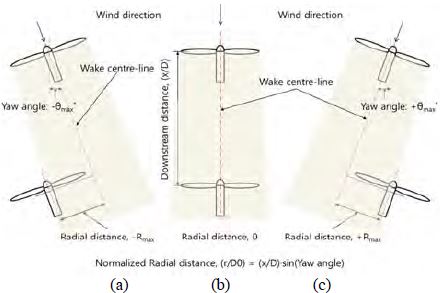
로터면적의 약 50%가 전방터빈의 후류영향을 받는 Case B-2 WT3, WT4 출력손실율이 전방풍력터빈 대비 최대 16.4 %로 낮은 변화율을 보임에 따라, 유사조건에서의 실측데이터와의 비교를 통해 해석결과의 타당성을 확인하고자 한다. Jeon et al. [12]은 제주도 성산풍력단지에서 약 2.5D의 이격 거리를 갖는 풍력터빈 2기(7-8호기)에 대한 출력감소율 비교분석에 관한 연구를 수행한 바 있다. 본 연구에서는 후류영향을 받는 후방터빈의 로터면적변화와 출력성능의 상관관계를 얻기 위해 Figure 9의 운전조건에서 측정된 장기간 SCADA 데이터 분석을 실시하였다. Figure 9(b)에 나타낸 바와 같이 후방터빈이 전방터빈 후류중심선과 수직 정렬되는 상태를 100% 후류영향을 받는 조건으로 정의하였으며, Figure 9(a), (c)와 같이 r/D = ±1.0(±R_max)인 상태에서는 후방터빈 로터면적의 50%가 후류영향을 받는다고 정의하였다. Figure 10은 무차원 반경거리(r/D) 변화에 따른 전·후방터빈의 출력성능 비교결과이며, r/D = 0 인 조건에서 후방터빈 출력은 약 73% 감소하고 r/D = ±1.0 인 조건에서의 전·후방터빈 출력차이는 크게 감소한다. Table 4에 비정상상태 CFD 해석결과와 성산풍력단지에서 측정된 SCADA데이터의 비교결과를 나타내었다.

Figure 9:

Definition of the radial distance in accordance with yaw angle

Figure 10:

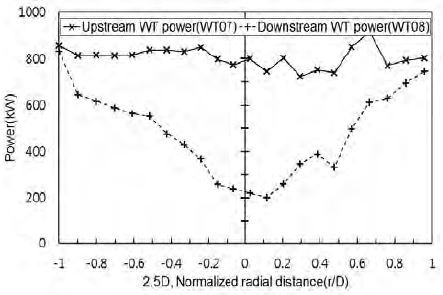
Power variations of the wind turbine pair according to the changes in the normalized radial distance

Table 4:

Comparison of SCADA and CFD analysis results

허브 중심단면에서의 속도 장(velocity contour) 분석결과, Case B-2 조건에서 후방터빈(WT4) 로터면적이 후류영역 50%(r/D = ±1.0)에 위치하는 것으로 확인되었다. Case B-2는 성산풍력단지에서 측정된 출력데이터의 풍속구간(7.5 ~ 9.5m/s)에 비해 다소 높은 풍속(11.7m/s)과 좁은 이격 거리(1.3D)를 갖기 때문에 측정데이터에 비해 다소 높은 출력감소율을 보인다. Case B-2 WT4의 출력은 전방터빈 대비 14% 감소되었으며, 유사한 조건의 성산풍력단지에서 측정된 후방터빈 출력감소율은 7% 수준으로 나타났다. 즉, 매우 가까운 이격 거리를 갖는 터빈배치조건에서도 로터의 50% 미만 영역이 후류영향에 노출될 경우에는 후방터빈의 출력감소율이 크지 않음을 확인하였다.

후방터빈이 전방터빈의 후류중심선에 정렬되는 CaseA-1 (1.4D), Case C-1(2.0D) 조건은 로터면적 100%가 후류영향에 노출된다. Case C-1 WT3의 출력감소율은 85.7%, 유사한 조건의 측정데이터는 73%의 매우 큰 출력감소율을 보였으며, Case C-1의 이격 거리가 2D로 더 짧기 때문에 더 높은 출력감소율을 보이는 것으로 판단된다. 특히 Table 4에 나타낸 바와 같이, 이격 거리가 증가 할수록 후류속도회복의 영향으로 출력감소율이 낮아지기 때문에 동일한 2.5D 조건에서는 측정데이터 수준의 출력감소율을 보여줄 것으로 예상된다.

4.3 연간발전량(Annual Energy Production, AEP) 계산

각각의 풍력터빈 배치조건에 대한 AEP 계산을 위해 식(1)의 레일리분포(Rayleigh distribution)를 확률밀도함수로 사용하였다. 레일리확률밀도함수는 척도계수(k)를 2로 가정한 후, 평균풍속만을 이용하여 풍속의 발생빈도를 추정한다. 여기서 f는 풍속(v)의 발생빈도, $$ \overline{v}$$는 평균풍속을 의미한다[13].

$\[ f\left(v\right)=\frac{\pi }{2}\frac{v}{\overline{v^2}}exp\left\{-\frac{\pi }{4}{\left(\frac{v}{\overline{v}}\right)}^2\right\} \]$

(1)

AEP(P_W)은 식 (2)을 이용하여 계산될 수 있으며, P(V)는 풍속구간별 출력, f(v)는 풍속(v)의 발생빈도이다. P(V)와 f(v)는 각각 비정상 CFD 해석결과의 평균출력과 레일리확률밀도함수를 이용하여 산정하였으며, 공기밀도는 1.225kg/m³, 가동율(availability)은 100%로 가정하였다.

$\[ P_W=\mathrm{8,760}hrs\times \sum \left[P\left(V\right)\times f\left(V\right)\right] \]$

(2)

본 연구에 사용된 풍력터빈의 운전풍속구간은 3m/s ~ 25m/s이지만, 4 cases(8m/s, 11.7m/s, 19m/s, 25m/s)의 풍속조건에 대한 CFD 해석만이 수행되었기 때문에 AEP 계산결과는 저 풍속구간(3 m/s ~ 8 m/s) 발전량을 포함하지 않는다. 특정 풍속구간에 대한 AEP 계산결과를 Table 5에 나타내었다. Case-A, Case-B, Case-C의 AEP는 각각 26.12GWh, 31.27GWh, 30.62GWh이며, 주 풍향을 기준으로 22.5°(CW)의 플랫폼 배치조건을 갖는 Case-B의 AEP가 가장 높게 나타났다. 특히 Case-B의 후방터빈들은 Case-A, C에 비해 후류영향을 덜 받기 때문에 AEP 측면에서 유리한 배치인 것으로 판단된다.

Table 5:

Comparison of AEP calculation results(8m/s ~ 25m/s)

Figure 2에 나타낸 바와 같이, 설치후보지역에서 높은 풍속 출현빈도를 보이는 풍향조건은 NNW, N, NW 이다. 본 연구에서는 높은 풍속 출현빈도를 보이는 풍향조건을 기준으로 Case-A ~ C 플랫폼의 배치각도 변화를 분석하기 위해Table 6에 풍향별 배치각도 변화를 시각적으로 표현하였다. 주 풍향 N과 NW 방위각에서는 Case-A, Case-C 배치에서 ‘□’ 형태가 나타나기 때문에 후방터빈들의 큰 출력손실이 예상되므로, Case-B 조건이 가장 효과적인 부유식 플랫폼 배치인 것으로 확인된다.

Table 6:

Platform installation angle for wind direction changes

5. 결 론

본 연구는 비정상 CFD 해석을 통해 다수 풍력터빈들의 배치조건변화에 따른 출력 및 연간발전량 분석을 수행하였고 주 풍향에 대한 최적 플랫폼 배치각도를 제안하였다.

정격이전 풍속조건의 경우, 전방터빈의 후류중심선에 위치하는 후방터빈(Case A-WT3, WT4, Case C-WT3)들의 출력이 85% 이상 감소하였고, 약 50%의 전방터빈 후류영향을 받는 후방터빈들(Case B-WT3, WT4)의 출력손실은 약 45% 수준으로 감소하였다. 정격풍속이후에서는 후방터빈 로터면적의 100%가 후류영향을 받는 조건에서 출력손실이 최대 15%로 나타났으나, 50%의 후류영향을 받는 조건에서는 최대 6% 수준의 비교적 낮은 출력손실을 보였다. 즉, 전후방터빈의 간격이 매우 좁은 플랫폼배치조건에서는 후방터빈 로터 50% 이상의 면적이 후류영향에 노출되지 않도록 하여야 한다.

풍력터빈 플랫폼 배치조건 별 출력성능 해석결과와 레일리분포를 이용하여 AEP를 계산하였으며 Case-B에서 가장 우수한 성능이 나타났다. 따라서 본 연구에서의 부유식 플랫폼은 북향(N)을 기준으로 22.5°의 각도로 설치되는 것이 AEP 측면에서 가장 적정한 배치안인 것으로 판단된다.

Acknowledgments

이 논문은 2016학년도 제주대학교 교원성과지원사업에 의하여 연구되었음

References

• B. Sanderse, Aerodynamics of Wind Turbine Wakes, Technical Report ECN-E-09-016, Energy research Centre of Netherlands, Netherlands, (2009).
• J. G. Schepers, ENDOW: Validation and Improvement of ECN’s Wake Model, Technical Report ECN-C-03-034, Energy research Centre of the Netherlands, Netherlands, (2003).
• R. J. Barthelmie, “Sixth framework programme, UpWind: Design limits and solutions for very large wind turbines”, European Wind Energy Association, p94-97, (2011).
• R. J. Barthelmie, S. T. Frandsen, K. Hansen, J .G. Schepers, K. Rados, W. Schlez, A. Neubert, L. E. Jensen, and S. Neckelmann, “Modelling the impact of wakes on power output at Nysted and Horns Rev,”, In European Wind Energy Conference, (2009).
• N. S. Choi, S. H. Nam, J. H. Jung, and K. C. Kim, “CFD study on aerodynamic power output of 6 MW offshore wind farm according to the wind turbine separation distance”, Journal of the Korean Society of Marine Engineering, vol. 35(no. 8), p1063-1069, (2011), (in Korean). [https://doi.org/10.5916/jkosme.2011.35.8.1063]
• B. S. Kim, M. E. Kim, and Y. H. Lee, “Predicting the aerodynamic characteristics of 2D airfoil and the performance of 3D wind turbine using a CFD code”, Transaction of Korean Society of Mechanical Engineers B, vol. 32(no. 7), p549-557, (2008), (in Korean). [https://doi.org/10.3795/ksme-b.2008.32.7.549]
• F. R. Menter, “Two-equation eddy-viscosity turbulence models for engineering applications”, AIAA Journal, vol. 32(no. 8), p1598-1605, (1994). [https://doi.org/10.2514/3.12149]
• Y. Cheng, F. S. Lien, E. Yee, and R. Sinclair, “A comparison of large eddy simulations with a standard k-εReynolds-averaged Navier-Stokes model for the prediction of a fully developed turbulent flow over a matrix of cubes”, Journal of Wind Engineering and Industrial Aerodynamics, vol. 91, p1301-1328, (2003). [https://doi.org/10.1016/j.jweia.2003.08.001]
• J. Sumner, C. S. Watters, and C. Masson, “CFD in Wind Energy: The virtual, multiscale wind tunnel”, Energies, vol. 3, p989-1013, (2010). [https://doi.org/10.3390/en3050989]
• F. R. Menter, M. Kuntz, and R. Langtry, “Ten years of industrial experience with the SST turbulence model”, Proceedings of the Turbulence, Heat and Mass Transfer 4, (2003).
• T. Tran, D. Kim, and J. Song, “Computational fluid dynamics analysis of a floating offshore wind turbine experiencing platform pitching motion”, Energies, vol. 8, p5011-5026, (2014).
• S. H. Jeon, B. S. Kim, and J. C. Hur, “Comparison and verification of wake models in an onshore wind farm considering single wake condition of the 2 MW wind turbine”, ENERGY, vol. 93, p1769-1777, (2015). [https://doi.org/10.1016/j.energy.2015.09.086]
• I. Kwon, J. Kim, I. Paek, and N. Yoo, “Variation of capacity factors by weibull shape parameters”, Journal of the Korean Solar Energy Society, vol. 33(no. 1), p32-39, (2013), (in Korean). [https://doi.org/10.7836/kses.2013.33.1.032]