고점도 실리콘오일 적용 점성댐퍼 동특성을 고려한 추진축계 최적 설계
Copyright © The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
최근 개발된 선박용 주기관은 추진효율 향상과 연료소비율 저감기술이 요구됨에 따라 과거에 비해 높은 비틀림진동 기진력 특성을 갖고 있다. 따라서 이를 제어하기 위해 기본적으로 엔진 선단에 점성 댐퍼나 점성-스프링댐퍼를 장착한다. 점성댐퍼의 경우 댐퍼 내부에 채워진 실리콘 오일이 탄성적인 연결이 없다고 가정하고 댐퍼설계를 하여 왔으나 고점도 실리콘 오일은 높은 점도에 따른 비틀림 강성이 존재할 뿐만 아니라 작동온도와 주파수에 따라 비선형적인 동특성을 갖는다.
본 논문에서는 고점도 실리콘 오일이 적용된 점성댐퍼의 동특성을 확인하고 해당 댐퍼가 장착된 축계의 비틀림진동 특성을 검토하였다. 이를 위해 점성댐퍼의 최적 동특성을 이론적으로 해석하는 방법을 검토하였고, 고점도 실리콘 오일로 채워진 점성댐퍼로 해당축계의 비틀림진동 제어를 하는 경우 댐퍼 작동온도 및 경년변화를 고려한 추진축계 최적 설계 방안에 대해서 검토하였다.
Abstract
The recently developed marine engines for propulsion of ships have higher torsional exciting force than previous engines to improve the propulsion efficiency and to reduce specific fuel oil consumption. As a result, a viscous damper or viscous-spring damper is installed in front of marine engine to control the torsional vibration. In the case of viscous damper, it is supposed that there is no elastic connection in the silicon oil, which is filled between the damper housing and inertia ring. However, In reality, the silicon oil with high viscosity possesses torsional stiffness and has non-linear dynamic characteristics according to the operating temperature and frequency of the viscous damper.
In this study, the damping characteristics of a viscous damper used to control the torsional vibration of the shafting system have been reviewed and the characteristics of torsional vibration of the shafting system equipped with a corresponding viscous damper have been examined. In addition, it is examined how to interpret the theoretically optimal dynamic characteristics of a viscous damper for this purpose, and the optimum design for the propulsion shafting system has been suggested considering the operating temperature and aging. when the torsional vibration of the shafting system is controlled by a viscous damper filled with highly viscous silicon oil.
Keywords:
Viscous damper, High-viscosity silicon oil, Aging phenomenon, Torsional vibration, Propulsion shafting system키워드:
점성 댐퍼, 고점도 실리콘 오일, 경년변화, 비틀림진동, 추진축계1. 서 론
최근 개발되는 선박용 엔진은 추진효율 향상을 위한 장행정화 및 연료소비율 저감기술이 요구되고 있으며 이에 따라 엔진 제조자들은 평균유효압력과 최고폭발압력을 꾸준히 증가시켜 왔다[1]. 하지만 이러한 노력은 비틀림진동 기진력을 상승시켜 비틀림 부가응력이 축계의 허용치를 초과하는 문제가 발생하고 있다. 이에 따라 보다 적극적으로 진동을 제어할 수 있는 방법이 요구되고 있으며, 기진력을 흡수할 있는 비틀림진동 댐퍼를 채택하여 비틀림진동을 제어하는 경우가 증가하고 있다[2].
비틀림진동 댐퍼로는 크게 동흡진기 기능을 갖는 고무댐퍼, 에너지 흡수형의 점성댐퍼, 이들의 기능을 조합시킨 점성-스프링댐퍼가 일반적으로 사용되고 있다. 고무댐퍼는 육상용 및 선박용의 소형 고속기관에 주로 적용되고 있으며, 점성-스프링댐퍼는 중·저속 기관의 비틀림진동 제어에 주로 사용되고 있다. 반면 점성댐퍼는 고속기관부터 대형 저속기관까지 다양하게 적용되고 있다[3][4].
진동제어를 위한 댐퍼를 설계하기 위해서는 댐퍼를 장착할 주진동계를 등가진동계로 모델링해야 한다. 이때 고무댐퍼 및 점성-스프링댐퍼는 강성계수와 점성감쇠계수를 모두 고려하는 반면 점성댐퍼는 점성감쇠만 있다고 가정하고 해석해 왔다[5][6]. 하지만 S. Iwamoto [7] 등의 연구결과에 의하면 고점도의 실리콘유를 갖는 점성댐퍼의 동특성은 감쇠계수를 복소 감쇠계수로 계산하여 점성감쇠와 강성계수를 함께 고려하는 모델링이 바람직하다고 보고하였다. 또한, M. S. Lee et al. [8], Y. N. Park et al. [9] 등은 고점도의 점성댐퍼를 갖는 기관축계의 비틀림진동을 측정하고 분석한 결과, 비선형진동의 일종인 도약현상(jump phenomenon)이 실선의 기관축계에서도 발생하고 있음을 보고하였다. 이는 점성댐퍼내의 실리콘유는 각속도에 비례하는 점성감쇠외에 각변위에 비례하는 선형강성계수와 각변위의 3승에 비례하는 비선형 강성계수도 함께 갖고 있는 것으로 판단된다. Tomoaki et al. [10]-[12] 등은 실리콘오일의 점도가 높을수록 고유진동수가 크게 변화될 뿐만 아니라, 고유진동수가 증가됨에 따라 댐퍼의 비틀림강성, 감쇠계수 및 실효 감소계수는 감소하고 댐퍼계수(damper coefficient)가 감소함에 따라 댐퍼의 비틀림 강성계수, 감쇠계수 및 실효 감쇠계수가 증가되는 경향이 있음을 점성댐퍼의 하우징과 관성링 각각 두곳에서의 비틀림진동 계측연구를 통해서 검증하였다. 뿐만 아니라, 일부 댐퍼 제작업체는 동점도가 최대 1,000,000 cSt/25°C에 달하는 초고점도의 실리콘오일까지 적용하고 있으며, 사용온도와 주파수 변화에 따른 강성계수와 점성 감쇠의 비선형적 특성을 제시하고 있다[13].
본 논문에서는 비틀림진동 제어를 위해 적용된 점성댐퍼의 동특성 및 성능을 이론적으로 해석하고, 해당축계에 최적 동특성을 갖는 점성댐퍼를 설계하여 비틀림진동 특성을 검토한다. 또한 점성댐퍼 모델링 방법에 따른 해석 결과를 비교 분석하여 점성댐퍼임에도 불구하고 실리콘 오일의 비선형 특성을 고려한 해석방법의 타당성을 검토하였다. 이외에도 실제 점성댐퍼가 부착된 축계를 대상으로 작동온도 변화 및 실리콘오일의 경년변화에 따른 점성댐퍼 동특성을 고려한 최적의 추진축계 설계 방안에 대해 검토하였다.
2. 고점도 실리콘 오일 적용 점성댐퍼 동특성
기본적으로 점성댐퍼의 하우징과 관성링 사이의 좁은 틈 사이에는 실리콘 오일로 채워져 있으므로 이 양자간에는 탄성적인 연결이 없다고 가정한다. 하지만 최근 일부 댐퍼제작업체에서는 동점도가 최소 0.65 cSt/25°C, 최대 1,000,000 cSt/25°C 범위까지 갖는 고점도 실리콘 오일을 적용하고 있다[13].
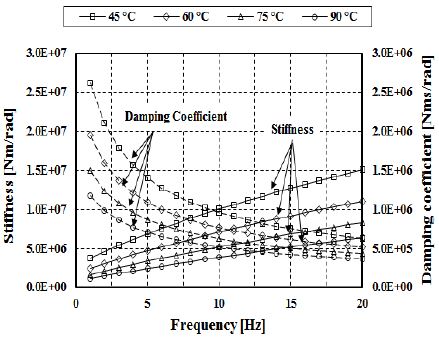
Figure 1은 점성댐퍼에 적용된 고점도 실리콘 오일의 특성을 보여주고 있다. 이 그림을 검토하여 보면 댐퍼의 작동온도 및 주파수에 따라 점성감쇠와 강성계수가 비선형적인 특성을 갖는것을 알 수 있다. 여기서 실선은 비틀림 강성계수를, 점선은 점성감쇠계수를 각각 나타낸다. 댐퍼의 작동온도에 따른 실리콘 오일의 동특성을 살펴보면, 작동온도가 상승함에 따라 비틀림 강성계수와 점성감쇠계수는 감소하는 경향이 있다. 또한, 진동수가 상승할 경우에는 비틀림 강성계수는 증가하는 반면 점성감쇠계수는 감소하는 경향이 있다. 따라서 댐퍼 제작업체는 온도변화에 따른 실리콘 오일의 동특성을 고려하여 실리콘 오일의 열부하 한계값을 제시해 주고 있으며 선박용의 경우 댐퍼 주위환경을 고려하여 최대 80°C ~ 90°C의 범위 이내에서 설계하도록 권장하고 있다. Table 1은 점성댐퍼에 적용된 작동기기별 실리콘 오일의 열부하 한계 온도를 보인다.
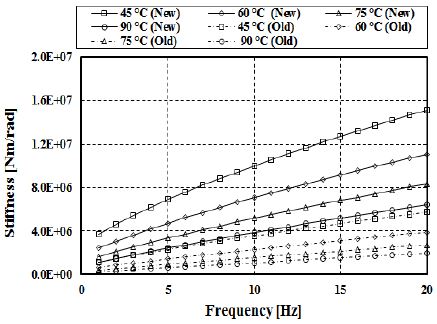
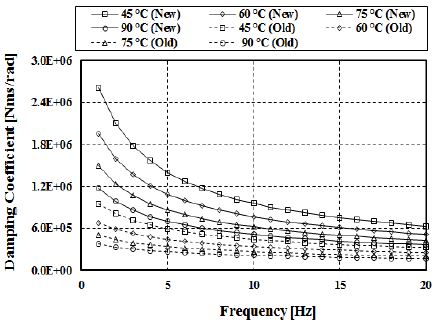
Figure 2 및 Figure 3은 실리콘 오일로 채워진 점성댐퍼의 경년변화에 의한 점성손실을 고려한 동특성을 보여주고 있다. 하우징과 관성링 사이 좁은 틈새에 채워진 실리콘 오일은 시간이 지남에 따라 내부에서 발생되는 분진에 의해서 실리콘 오일의 점성이 초기에 비해 50% 정도 감소하며, 이는 동일 작동온도에서 비틀림 강성계수 및 점성감쇠계수를 감소시킨다.
3. 점성댐퍼 최적 설계 이론
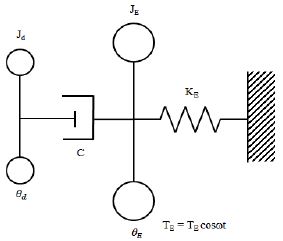
엔진의 비틀림진동을 점성 댐퍼로 제어하는 경우, 먼저 엔진을 다자유도 진동계로 모델링하여 고유각진동수와 상대 진폭비를 구하고 이를 등가의 1자유도계로 치환한다. 이와 같이 1자유도계로 치환된 추진축계에 댐퍼를 장착하면 Figure 4와 같이 등가 2자유도계로 된다[14]-[19].
점성댐퍼와 축계 시스템을 2질점계의 등가 집중질량계로 치환하면 최적 점성댐퍼의 동특성은 다음과 같이 유도할 수 있다. 먼저 이 진동계의 운동방정식은 다음과 같다.
| (1) |
| (2) |
JE Moment of inertia for main vibration system
Jd Moment of inertia for damper ring
KE Torsional stiffness of main vibration system
c Damping coefficient of damper
θE Angular amplitude of main vibration system
θd Angular amplitude of damper ring
따라서 동배율 MR 을 구하면 식 (3)와 같다.
| (3) |
동배율 MR 이 감쇠계수비 ζ 와 무관하게 되는 강제진동수비 g 는 다음과 같다. 여기서, 질량비 R 은 댐퍼링의 관성모멘트 Jd 를 등가관성모멘트 JE 로 나눈 값이다.
| (4) |
이때의 동배율은 식 (5)과 같이 된다.
| (5) |
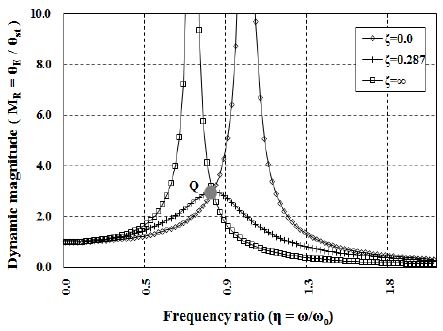
Figure 5는 질량비 R를 1로하고 감쇠계수비 ζ 를 변수로 하여 그린 동배율곡선이다. 보는 바와 같이 Q점은 감쇠계수비 ζ 에 상관없이 모든 곡선이 통과된다.
진동계에 감쇠장치를 부가하는 것은 공진 진폭의 정점을 가능하면 낮게 하기 위함이므로 이를 위해서는 댐퍼의 감쇠를 적절하게 선정하여야 한다. 점성댐퍼가 최적이 되기 위해서는 Q점에서 동배율이 극대값을 갖는 감쇠비 ζ 를 구해야 한다. 이를 위해 식 (5)를 강제진동수비 g 에 대하여 미분하고 이 값이 0이 되는 최적 감쇠비 ζopt 를 구하면 식(6)과 같다.
| (6) |
4. 점성댐퍼 동특성을 고려한 추진 축계 최적 설계 방안
본 장에서는 고점도 실리콘 오일로 채워진 점성댐퍼를 적용한 추진축계를 대상으로 비틀림진동의 특성을 분석하고 해당 축계의 최적 설계 방안에 대해 검토한다. 점성댐퍼는 댐퍼 관성링이 주진동계와 동조하여 진동제어를 하기 때문에 시간이 경과됨에 따라 댐퍼 내부에서 발생되는 분진에 의해서 실리콘 오일 점성이 감소하게 되어 댐퍼 성능이 떨어지게 된다. 또한, 엔진의 초기 기동 후 MCR(Maximum Continuous Rating)까지 출력을 상승시킬 때는 충분한 예열이 되지 않는 상태에서 점성댐퍼가 작동하게 된다. 일반적으로 축계 설계자는 점성댐퍼가 상기와 같은 현상이 발생할 것을 예상하지 않고 해당 축계의 비틀림진동을 제어하도록 설계하고 있다. 따라서 고점도 실리콘 오일을 적용한 점성댐퍼를 장착한 선박의 추진축계는 상기와 같은 상황에 따른 축 피로손상이 발생되지 않도록 적절한 방안이 마련되어야 한다. 여기서는 고점도 실리콘오일로 채워진 점성댐퍼를 적용한 축계를 대상으로 작동온도 및 경년변화에 따른 비틀림진동 특성을 살펴보고 최적의 축계 설계방안에 대해 검토하였다.
Table 2는 대상 축계의 요목을 나타낸다. 이 축계의 비틀림진동 해석 결과는 1절 비틀림진동의 절점이 중간축에 존재하고, 중간축의 부가응력이 높아 선급에서 제시하는 피로한도 및 항복응력에 대한 기준치를 상회하고 있다. 따라서 이 선박의 축계 설계자는 중간축에 걸리는 부가응력을 낮추기 위해서 점성댐퍼를 엔진 선단에 장착하여 비틀림진동을 제어하였다. Table 3는 이 선박의 축계 설계자가 선정한 점성댐퍼의 요목을 보여주고 있다. 여기서 점성댐퍼 모델링 방법을 달리하여 실리콘 오일의 고점도화가 축계 비틀림진동 특성에 미치는 영향을 검토하였다. Case I은 점성댐퍼 최적 설계이론에 입각하여 하우징과 관성링 사이에 탄성적인 연결이 없다고 간주하고 최적 감쇠계수를 적용한 것이고, Case II는 고점도 실리콘 오일의 동특성을 고려하여 최대 작동온도 90℃를 기준으로 비틀림 강성계수를 고려한 것이다.
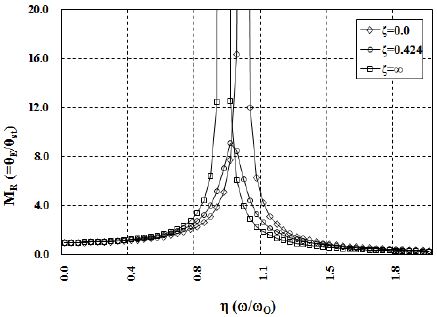
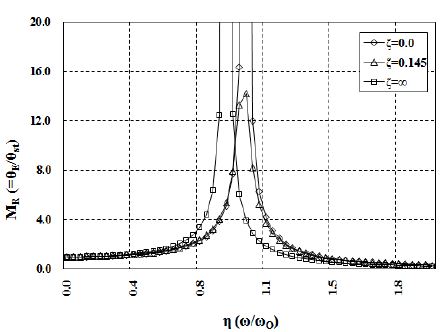
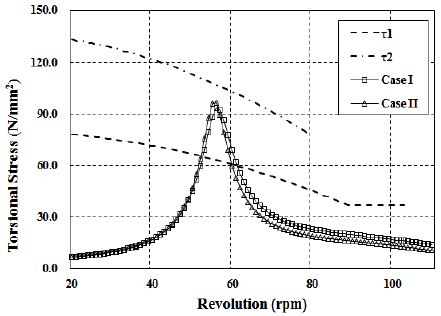
Figure 6은 대상 선박의 추진 축계에 Table 3의 점성댐퍼를 장착한 경우의 중간축에 대한 비틀림진폭 해석 결과이다. 이 그림을 검토하여 보면 동배율이 14.2로 상당히 높다. 따라서 점성댐퍼의 관성질량은 그대로 두고 3장에서 기술한 점성댐퍼의 최적 설계이론에 따라 최적 감쇠계수비를 구하면 0.414로 된다. 이는 본 축계에 장착된 점성댐퍼의 점성감쇠계수비에 비해 2.93배에 해당한다. Figure 7은 최적 댐퍼 설계이론에 따라 구한 감쇠계수를 갖는 점성댐퍼 장착시의 비틀림 동배율 해석 결과이다. 이 그림을 검토하여 보면 동배율이 9.1으로 기존의 동배율 대비 64.1% 정도 감소한다. Figure 8은 중간축에 작용하는 비틀림응력 해석 결과를 나타내며, 이를 검토하여 보면 Case I은 중간축에 작용하는 비틀림 부가응력이 56 rpm에서 최대값이 96.7 N/㎟으로 Case II 대비 3.3 N/㎟ 증가하지만 위험회전수범위는 2 rpm 감소한다.
다음은 점성댐퍼의 작동온도에 따른 고점도 실리콘 오일의 동특성의 변화가 해당 축계에 미치는 영향을 확인하기 위해 점성댐퍼 작동온도를 45℃ ~ 90℃까지 변화시키면서 축계 비틀림진동 특성을 검토하였다. 여기서 점성댐퍼에 적용된 실리콘 오일의 동특성은 Figure 1에 보이는 바와 같으며, Figure 9는 중간축에 걸리는 부가응력 해석 결과이다. 이들 그림을 검토하여 보면 엔진이 정상 작동 후 댐퍼 주위온도가 충분히 상승하여 댐퍼 작동온도가 90℃에 도달할 경우에는 비틀림 부가응력이 선급에서 제시하는 항복응력에 대한 기준치(τ2) 대비 13%의 설계 마진을 갖는다. 하지만 댐퍼의 작동온도가 45℃일 때에는 비틀림 부가응력이 항복응력에 대한 기준치(τ2)에 근접한다. 이때는 댐퍼가 충분히 예열이 되지 않는 상태에서 댐퍼가 작동하는 경우로 엔진의 초기 기동시에 발생할 수 있다. 특히나 선박이 동절기나 빙하해역을 항해하고자 하는 경우에는 더욱 심각한 상황에 놓이게 된다. 따라서 중간축에 걸리는 비틀림 부가응력을 낮추기 위해 점성댐퍼 설계 주요파라미터인 점성감쇠계수를 조정하여 검토하였다. 이 결과를 Figure 10에 보인다. 이 그림을 검토하여 보면 점성감쇠계수를 기존 대비 10% 저감할 경우에는 점성댐퍼의 작동온도가 45℃인 경우에도 비틀림 부가응력이 항복응력에 대한 기준치(τ2)에서 5.6% 설계 마진을 확보할 수 있는 것을 알 수 있다.
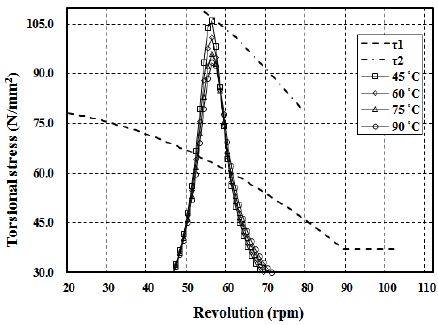
Comparison of 5th order torsional stress in intermediate shaft according to varied operating temperature of viscous damper
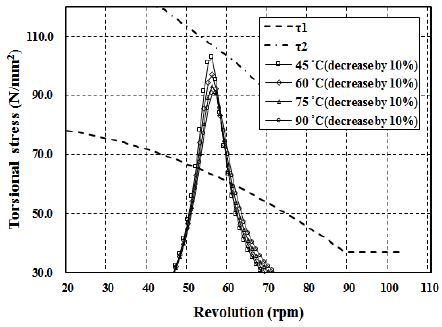
Comparison of 5th order torsional stress in intermediate shaft according to reduced damping coefficient of viscous damper by 10%
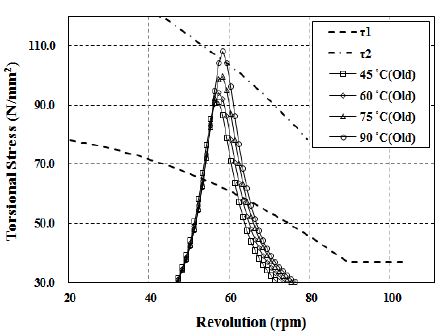
Comparison of 5th order torsional stress in intermediate shaft according to varied operating temperature at aging condition
다음은 점성댐퍼 하우징과 관성링 사이 틈새에 채워진 실리콘 오일의 경년변화가 축계 비틀림진동 특성에 미치는 영향을 검토하였다. 여기서 점성댐퍼에 적용된 실리콘 오일의 동특성은 Figure 2 및 3에 보이는 바와 같으며, Figure 10은 중간축에 걸리는 부가응력 해석 결과이다. 이때 경년변화에 따른 실리콘 오일의 점성손실은 초기 대비 50%를 조건으로 하였다. 이를 검토하여 보면 실리콘 오일의 점성손실은 동일 작동온도에서 공진점을 상향시킨다. 또한 실리콘 오일의 점성 손실이 50%까지 발생한 경우에는 중간축에 걸리는 비틀림 부가응력이 초기 대비 반대의 경향을 보인다. 즉, 실리콘 오일의 점성손실이 없을 경우에는 점성댐퍼의 작동온도가 45℃일 때 중간축에 걸리는 비틀림 부가응력이 선급에서 제시하는 항복응력에 대한 기준치(τ2)를 상회하는 반면 실리콘 오일의 점성손실이 발생한 경우에는 오히려 점성댐퍼의 작동온도가 90℃일 때 기준치를 상회한다. 이와 같이 점성댐퍼 하우징과 관성링 사이 틈새에 채워진 실리콘 오일은 시간 경과에 따라 점성 손실이 발생하게 되며, 최대 50%의 점성손실이 발생한 경우 댐퍼의 제진성능이 저하되어 축 피로손상을 야기할 우려가 있다.
일반적으로 최적 댐퍼 설계이론을 적용한 점성댐퍼를 엔진 선단에 장착함으로써 축계 비틀림진동을 제어할 수 있다. 하지만 고점도 실리콘 오일을 적용한 점성댐퍼를 장착한 경우에는 최적댐퍼 설계이론만으로는 효과적으로 비틀림진동을 제어하는데 한계가 있다. 이러한 경우에는 최적댐퍼 설계이론보다는 상기와 같이 작동온도에 따른 실리콘 오일 동특성 변화와 점성손실을 고려하여 축계 비틀림진동 제어를 하는게 적절하다. 보통의 경우 축계 설계자는 점성댐퍼가 상기와 같은 현상이 발생할 것을 예상하지 않고 해당 축계를 설계한다. 이러한 경우 중간축은 IACS UR M68[20]에 따라 결정된 중간축의 항복응력에 대한 기준치보다 10% ~ 15%정도 여유를 갖도록 설계된다. 하지만 고점도 실리콘 오일을 적용한 점성댐퍼를 이용하여 축계 비틀림진동 제어를 하는 경우에는 축계 설계자는 중간축에 작용하는 비틀림 부가응력이 기준치보다 20% ~ 30%정도 여유를 갖도록 설계해야 한다. 이렇게 함으로써 댐퍼 작동온도 및 실리콘 오일의 경년변화의 영향에 따라 해당축에 작용하는 비틀림 부가응력이 항복응력에 대한 기준치를 넘는 일이 없도록 하여 선박 사용수명(25년~30년)내에 축 피로손상이 발생하지 않도록 할수 있다.
5. 결 론
본 연구에서는 고점도 실리콘 오일이 적용된 점성댐퍼의 동특성을 확인하고, 해당 댐퍼가 장착된 축계의 비틀림진동 특성을 검토한다. 이를 위해 점성댐퍼의 최적 동특성을 이론적으로 해석하는 방법을 검토하였고, 고점도 실리콘 오일로 채워진 점성댐퍼로 해당 축계의 비틀림진동 제어를 하는 경우 댐퍼 작동온도 및 경년변화를 고려한 축계 최적 설계 방안을 제시하였다. 이를 요약하면 다음과 같다.
- (1) 기본적으로 점성댐퍼의 하우징과 관성링 사이의 좁은 틈 사이에는 실리콘 오일로 채워져 있으므로 이 양자간에는 탄성적인 연결이 없다고 가정한다. 하지만 실리콘 오일의 고점도화에 따라 비틀림 강성이 존재하며 이는 댐퍼 작동온도와 주파수에 따라 비선형적으로 변화하는 특성을 가지고 있다. 즉, 작동온도가 상승할수록 비틀림 강성계수와 점성감쇠계수는 감소하지만, 진동수가 상승할 경우에는 비틀림 강성계수는 증가하는 반면 점성 감쇠계수는 감소하는 경향이 있다.
- (2) 일반적으로 최적 댐퍼 설계이론을 적용하여 설계한 점성 댐퍼는 축계 비틀림진동을 효과적으로 제어할 수 있다. 그러나 최근 점성댐퍼에 적용되고 있는 고점도 실리콘 오일은 작동온도에 따라 동특성이 변화되는 특성이 있어 최적 댐퍼 설계이론으로는 축계의 비틀림진동을 효과적으로 제어하는데는 한계가 있다. 특히 댐퍼의 작동온도가 떨어질 경우에는 축에 걸리는 부가응력이 선급에서 제시하는 항복응력에 대한 기준치(τ2)를 상회할 우려가 있다.
- (3) 고점도 실리콘 오일은 시간이 경과함에 따라 댐퍼 내부에서 발생되는 분진에 의해서 점성 손실이 발생한다. 이는 초기 상태에 비해 비틀림 강성계수와 점성 감쇠계수를 감소시키며, 이러한 상황은 댐퍼의 작동온도가 상승함에 따라 축에 걸리는 부가응력을 증가시킨다. 따라서 선박 운항중에 축계의 비틀림 부가응력이 선급에서 규제하는 항복응력에 대한 기준치(τ2)를 초과하여 축에 피로손상이 발생할 수 있다.
- (4) 고점도 실리콘 오일로 채워진 점성댐퍼로 축계 비틀림진동 제어를 하는 경우에는 점성댐퍼의 낮은 작동온도에 따른 실리콘 오일의 동특성 변화와 경년변화에 따른 점성손실의 영향을 고려하여 축계 설계를 하면 해당 축계의 비틀림 부가응력이 효과적으로 제어될 수 있음을 확인하였다.
References
- Y. G. Kim, S. J. Hwang, J. S. Sun, S. G. Jung, and U. K. Kim, “A study on the effect of torsional vibration for propulsion shafting due to the characteristics of fuel saving marine engine”, Proceedings of the 39th the Korean Society of Marine Engineering Fall Conference, p186, (2015), (in Korean).
- Y. G. Kim, S. J. Hwang, Y. H. Kim, K. H. Cho, and U. K. Kim, “A control of torsional vibration for propulsion shafting by optimum design of viscous damper applying silicon oil with high viscosity”, Proceedings of the 40th the Korean Society of Marine Engineering Spring Conference, p172, (2016), (in Korean).
- C. K. Lee, and H. J. Jeon, “A study on the design of the torsional vibration viscous damper for the crankshaft and developing of its performance simulation computer program”, Journal of the Korean Society of Marine Engineering, vol. 13(no. 1), p77-96, (1989), (in Korean).
- H. J. Jeon, Y. J. Kim, D. H. Kim, and U. K. Kim, “A study on the torsional vibration damper of the small internal combustion engine driving system (Part I) -Development of the optimum viscous-rubber damper-”, Journal of the Korean Society of Marine Engineering, vol. 15(no. 2), p44-52, (1991), (in Korean).
- T. E. Kim, A Study on the Torsional Vibration Characteristics and Control for the Shafting Systems with Middle and High Speed Diesel Engine, M.S. Thesis, Department of Mechanical Engineering, Korea Maritime University, Korea, (1999), (in Korean).
- D. C. Lee, A Study on the Vibration Control of the Engine Body and Shafting System for a Large Scale Diesel Engine”, Ph.D. Dissertation, Department of Mechanical Engineering, Korea Maritime University, Korea, (1995), (in Korean).
- S. Iwamoto, “The development of the torsional vibration damper of viscous type with controllable elasticity effect”, Journal of the Marine Engineering Society in Japan, vol. 15(no. 1), p19, (1973).
- Y. N. Park, C. W. Ha, U. K. Kim, H. J. Jeon, “A study on the stability analysis and non-linear forced torsional vibration for the engine shafting system with viscous damper”, Proceedings of the Fall Conference of the Korean Society for Noise and Vibration Engineering, p282-287, (1996), (in Korean).
- M. S. Lee, A Study on the Nonlinear Torsional Forced Vibration for the Engine Shafting Systems Modeled with Multi-Degree-of-Freedom, M.S Thesis, Department of Mechanical Engineering, Korea Maritime University, Korea, (1999), (in Korean).
-
T. Kodama, K. Wakabayashi, Y. Honda, and S. Iwamoto, “Dynamic characteristics of viscous-friction dampers by simultaneous vibration displacement measurement at two points”, SAE 2001 World Congress, SAE paper No.2001-01-0281(2001), p1-12, (2001).
[https://doi.org/10.4271/2001-01-0281]

- T. KODAMA, K. WAKABAYASHI, Y. HONDA, “An experimental study on the dynamic characteristics of torsional viscous-friction dampers for high-speed diesel engine -Relationship between damper clearance and kinematic viscosity of silicone fluid-”, Japan Socirty of Mechanical Engineers, Dynamics and Design Conference 2001, (2001), (in Japanese).
- T. KODAMA, K. WAKABAYASHI, Y. HONDA, and S. IWAMOTO, “An experimental study on dynamic characteristics of torsional stiffness and torsional damping coefficient of viscous-friction damper”, Transactions of the Kokushikan University, Faculty of Engineering, (no. 35), p67-79, (2002).
- Bohmeyer, Simulation Report, Hasse & Wrede, Germany, (2012).
- H. J. Jeon, and U. K. Kim, Machine Dynamics, Hyo-sung publisher, (1999), (in Korean).
- H. J. Jeon, and D. C. Lee, Vibration of Propulsion Shafting, Dasom publisher, (2003), (in Korean).
- T. Osamu, and S. Suei, Mechanical Vibration Theory, Corona publishing co., ltd., (1951), (in Japanese).
- S. Maezawa, Vibration Engineering, Morikita publishing co., ltd., (1976), (in Japanese).
- W. K. Wilson, Practical Solution of Torsional Vibration Problems, vol. 1-5, Chapman & Hall, London, (1942).
- BICERA, Handbook of Torsional Vibration, Cambridge University Press, (1958).
- IACS, M68: Dimension of propulsion shafts and their permissible torsional vibration stresses, available at: http://www.iacs.org.uk Accessed September 29, 2016.