Numerical analysis of natural convection heat transfer from a fin in parallel enclosure

1. Introduction

The numerical estimation of natural convection from a fin is an element of heat transfer problems. Basically, two-dimensional analysis is fundamental. Furthermore, if the introduction of a boundary-fitted coordinate system under the conformal mapping is possible, then this problem is reduced simply to a boundary-value problem, very similar to a Cartesian coordinate system, resulting in possibility of spectral decomposition [1]. Many theories and applications on conformal mapping have been presented in the past [2]-[5].

Among many numerical schemes for heat and fluid flow analysis, the spectral finite difference scheme using the conformal mapping [1] is very effective, although the special attention is required in a multiply-connection region [6], which is the case described in this paper. This spectral finite difference scheme has a good resolution in space and a high computation speed. Also, this scheme can cover various problems associated with infinite extension [7] and support the mixed types of boundary conditions [1][8]. From the viewpoint of experimental work, the heat transfer from fins in plane layers is treated by authors of references [9]-[13].

The spectral finite difference scheme developed by one of authors earlier [1][14] has the following features. For a coordinate system under analysis, the boundary-fitted-coordinate system using the conformal mapping is adopted, where all the boundaries in a two-dimensional problem, including infinity, if any, constitute a part or whole of one or two coordinate surfaces for the same component of one independent variable so that it can be reduced to a boundary-value problem (at least Dirichlet type, Neumann type, or mixed type [8]). If a part does not correspond to a physical boundary, it is necessary to introduce additional conditions such as continuity of scalars. Generally, such a conformal mapping is not necessarily unique, and a sufficient method to apply it for any configuration is not yet known.

Secondly, Fourier series is frequently used for the spectral decomposition of dependent variables, but is not restricted. In some cases, analytical solutions (at least first two terms [7] and asymptotic solution [15]) are obtained without any aid of finite difference approximation.

Thirdly, the condition of multiply-connectedness is exactly introduced in a mathematical point of view [1]/[14][15]; such a condition is not in the conventional FEM (Finite element method) and FDM (finite difference method). Decomposition of the governing equations exactly depends on mathematical theorems (usually depending on necessary and sufficient conditions), which does not introduce errors. Nevertheless, it is assumed that higher components decay faster, which means that the conditional convergence of series is not adequate for numerical solutions. The conventional FEM and FDM produce error(s) in formulation unless polynomial solutions are expected. Experimental values may be sensitive to conditions, not expressed explicitly, which can be covered by the present method in some cases [16].

Authors have been performing several works on natural convection heat transfer [17]-[19]. In this study, the numerical analysis of two-dimensional laminar natural convection heat transfer from a fin in the parallel enclosure is carried out by a spectral finite difference scheme.

2. Analysis

2.1 Configuration

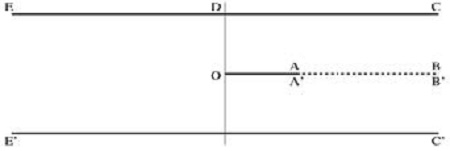
Two-dimensional laminar natural convection in a vertical plane is considered in this study. Fluid is assumed to be enclosed between two horizontal parallel plates (CE and C’E’) of infinite extension equipped with a horizontal finite length fin(infinitesimally small thickness, upper surface OA, lower surface OA’) exactly in the middle of the plates as shown in Figure 1.

Figure 1:

Schematic configuration

The boundary-fitted conformal mapping coordinate system (α, β) is introduced such that

(1)

where (x, y) is a dimensionless Cartesian coordinate system with vertically upward y. In this system, the reference length, L, is given by the distance between two parallel plates, i.e., the upper and lower plates are given by y= 0.5 and y= −0.5 respectively. It is assumed that the point (α, β) = (0, 0) corresponds to point O, and (α, β) = (0, π/2) to point A. Consequently, the upper plate is designated by α = 0, 2 tan⁻¹(1/$$ \sqrt{1-{\mathit{k}}^2}$$) < β < π, the lower plate by α = 0, −π < β < −2 tan⁻¹(1/$$ \sqrt{1-{\mathit{k}}^2}$$) and the fin by α = 0, −π/2 ≤ β ≤ π/2. The centerline AB (or A’B’) corresponds to α = 0, π/2 < |β| < 2 tan⁻¹(1/$$ \sqrt{1-{\mathit{k}}^2}$$). The system of governing equations for substantially incompressible Newtonian fluids under a Boussinesq approximation consists of the equation of vorticity transport, the relationship between vorticity ζ and stream function ψ, and energy equation:

$\[ \begin{array}{c}\frac{J}{r^2}\frac{\partial \zeta }{\partial t}+\frac{1}{r}\frac{\partial \left(\zeta ,\psi \right)}{\partial \left(r,\beta \right)}=\\ \frac{1}{\sqrt{\mathit{Gr}}}\left(\frac{{\partial }^2}{\partial r^2}+\frac{1}{r}\frac{\partial }{\partial r}+\frac{1}{r^2}\frac{{\partial }^2}{\partial {\beta }^2}\right)\zeta +\frac{1}{r}\frac{\partial \left(T,y\right)}{\partial \left(r,\beta \right)}\end{array} \]$

(2)

$\[ \begin{array}{c}\frac{J}{r^2}\zeta +\left(\frac{{\partial }^2}{\partial r^2}+\frac{1}{r}\frac{\partial }{\partial r}+\frac{1}{r^2}\frac{{\partial }^2}{\partial {\beta }^2}\right)\psi =0\\ \frac{J}{r^2}\frac{\partial T}{\partial t}+\frac{1}{r}\frac{\partial \left(T,\psi \right)}{\partial \left(r,\beta \right)}=\frac{1}{Pr\sqrt{Gr}}\left(\frac{{\partial }^2}{\partial r^2}+\frac{1}{r}\frac{\partial }{\partial r}+\frac{1}{r^2}\frac{{\partial }^2}{\partial {\beta }^2}\right)T\end{array} \]$

(3)

$\[ \begin{array}{c}J\equiv \frac{\partial \left(x,y\right)}{\partial \left(r,\beta \right)},r\\ \equiv e^{\alpha }\end{array} \]$

(4)

Through Equation (1):

$\[ \frac{\sqrt{J}}{r}=\frac{\left(1-k^2\right)e^{-\alpha }}{2\pi }=\times \left|\frac{\frac{{\text{tanh}}^2\left(\alpha +i\beta \right)}{2}}{\frac{{\text{cosh}}^2\left(\alpha +i\beta \right)}{2}+\frac{{\left(1-k^2\right)\text{sinh}}^2\left(\alpha +i\beta \right)}{2}}\right| \]$

(5)

3. Numerical results and discussion

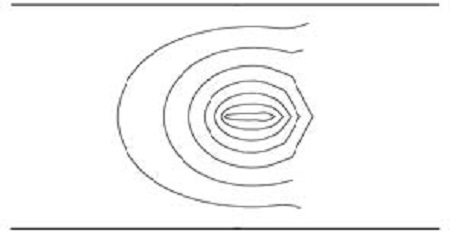
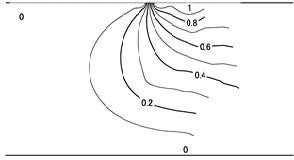
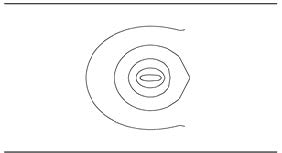
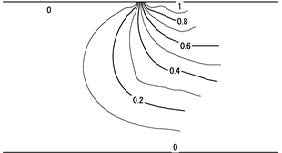
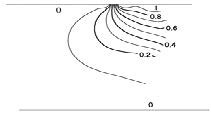
Figures 2 and 3 show streamlines and isotherms at $$ \sqrt{1-{\mathit{k}}^2}$$ = 0.9, T_c = 0.35, Gr = 10, and Pr = 0.7 (fin width = 0.264) respectively, where the characteristic values are Nu_m = 0.32, F = 0.070i, and c = −0.0075. c < 0 presents clockwise circulation. For not a sufficiently large Grashof number, Gr, the characteristic values are nearly insensitive to Pr. Figures 4 and 5 show streamlines and isotherm at $$ \sqrt{1-{\mathit{k}}^2}$$ = 0.8, T_c = 0.35, Gr = 10, and Pr = 0.7 (fin width = 0.163) respectively, where the characteristic values are Nu_m = 0.49, F = 0.398i, and c = −0.028. Figure 6 shows isotherms at $$ \sqrt{1-{\mathit{k}}^2}$$ = 0.9, T_c = 0.15, Gr = 10, and Pr = 0.7, where the characteristic value are Nu_m = −0.52, F = 0.039i, and c = −0.043.

Figure 2:

Streamlines at 1-k2 = 0.9, Tc = 0.35, Gr = 10, Pr = 0.7 and δψ = −0.001

Figure 3:

Isotherms at 1-k2 = 0.9, Tc = 0.35, Gr = 10 and Pr = 0.7

Figure 4:

Streamlines at 1-k2 = 0.8, Tc = 0.35, Gr = 10, Pr = 0.7 and δψ= −0.005

Figure 5:

Isotherms at 1-k2 = 0.8, Tc = 0.35, Gr = 10 and Pr = 0.7

Figure 6:

Isotherms at 1-k2 = 0.9, Tc = 0.15, Gr = 10 and Pr = 0.7

Undisturbed (without any fin) pure conduction temperature distribution is given by

which shows that T_c at O is 0.25. Thus, as long as $$ \sqrt{1-{\mathit{k}}^2}$$ is not very near unity, the fin would behave as a heat source if T_c > 0.25, and as a heat sink if T_c < 0.25, which is coincident with Figures 3 and 6.

4. Conclusions

Natural convention heat transfer from a two-dimensional fin in the parallel enclosure was successfully analyzed, using a spectral finite difference scheme, supplemented with a condition of doubly-connectedness of the domain. The enclosure plates were placed horizontally and kept at constant temperatures. Problems were treated as a boundary-value problem, and variables were exactly decomposed into Fourier components. To get a steady-state solution, a time-marching scheme was applied. Depending on the uniform surface temperature of fin, the fin behaved as a heat source or sink.

References

• Y. Mochimaru, , “Effectiveness of a spectral finite difference scheme”, Computational Fluid Dynamics Review, 1, p379-394, (1998). [https://doi.org/10.1142/9789812812957_0021]
• L. I. Volkovyskii, G. I. Lints, and I. G. Aramanovich, “A collection of problems on complex analysis”, Pergamon Press, (1965).
• P. Henrici, Applied and Computational Complex Analysis, 1, Wiley, (1974).
• L. N. Trefethen, Numerical Conformal Mapping, North-Holland, (1986).
• R. Schinzinger, and P. A. A. Laure, Conformal Mapping, Elsevier, (1991).
• Y. Mochimaru, “Existence/non-existence of conformal mapping in some family of functions”, International Journal of Pure and Applied Mathematics, 49, p497-503, (2008).
• Y. Mochimaru, “Analytical treatment of far away field behavior”, Computational Fluid Dynamics Journal, 13, p422-426, (2004).
• Y. Mochimaru, “Extension of applicability of a spectral finite difference scheme to mixed boundary conditions”, Transport Phenomena in Thermal-Fluids Engineering, p315-320, (1996).
• I. Catton, Kankaç, Aung, Vskanta, Natural Convection in Horizontally Unbounded Plane Layers, Natural Convection, Fundamentals and Applications, Hemisphere Pub, p97-134, (1985).
• F. A. Kulacki, and D. E. Richards, Kankaç, Aung, Vskanta, Natural Convection in Plane Layers and Cavities with Volumetric Energy Sources, Natural Convection, Fundamentals and Applications, Hemisphere Pub, p179-255, (1985).
• R. Viskanta, Kankaç, Aung, Vskanta, Natural Convection in Melting and Solidification, Natural Convection, Fundamentals and Applications, Hemisphere Pub, p845-877, (1985).
• P. G. Simpkins, and K. S. Chen, Kankaç, Aung, Vskanta, Natural Convection in Horizontal Containers with Applications to Crystal Growth, Natural Convection, Fundamentals and Applications, Hemisphere Pub, p1010-1032, (1985).
• A. G. Bathelt, and R. Viskanta, “Heat transfer and interface motion during melting and solidification around a finned heat source/sink”, Transactions of ASME, Journal of Heat transfer, 3, p720-726, (1981). [https://doi.org/10.1115/1.3244532]
• Y. Mochimaru, “A spectral finite difference scheme and its effectiveness”, Proceedings of 26th Annual Iranian Mathematics Conference, p245-254, (1995).
• Y. Mochimaru, “Global instability of natural convection in an elliptic cavity, Using a fourier spectral difference method”, 7th Int. Coll. on Differential Equations, p243-252, (1997).
• D. Akita, and Y. Mochimaru, “Numerical simulation of a flow past an elliptic cylinder at moderately high reynolds numbers”, CMMPG, 1, p1-7, (2015).
• Y. Mochimaru, and M. W. Bae, “A study on natural convection from two cylinders in a cavity”, Journal of Mechanical Science and Technology, 20(10), p1773-1778, (2006). [https://doi.org/10.1007/BF02916281]
• Y. Mochimaru, and M. W. Bae, “Natural convection heat transfer in a doubly - connected region, using a spectral finite difference scheme”, International Journal of Pure and Applied Mathematics, 32(1), p51-60, (2006).
• Y. Mochimaru, and M. W. Bae, “Spectral analysis on natural convection heat transfer from a rectangular cylinder partially heated in an infinite extension (Invited Lecture)”, International Journal of Pure and Applied Mathematics, 46(2), p237-243, (2008).