저속으로 전복되는 선박사고의 선체 특성에 대한 해석적 연구

2.1 정상 시의 선체운동

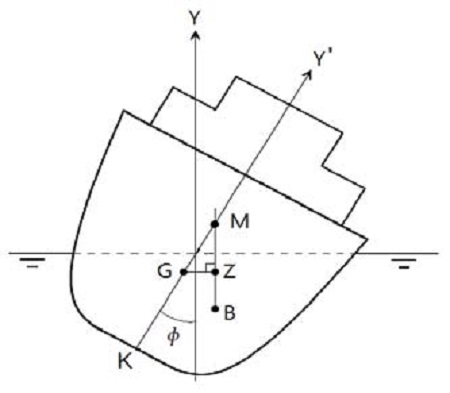
Figure 1은 정상 상태의 선체 경사각이 φ일 때 부심 B와 메타센터 M의 관계를 나타내며 무게중심 G와의 거리인 GM은 양의 방향으로 작용하고 있다.

Figure 1:

Schematic diagram to describe GM and GZ

GZ는 G와 BM 간 거리로서 복원모멘트의 팔길이에 해당하며 이를 φ의 함수인 GZ(φ)라 하면 평온한 해상상태에서 선체 경사각 φ는 다음의 운동식으로 나타낼 수 있다[1]-[3].

여기서 J는 횡운동 관성모멘트, b는 선형값인 선체 횡운동 감쇠계수(Damping coefficient)이고 ∆와 g는 배수량과 중력가속도이다. 한편, φ가 작은 범위에서는GZ(φ) ≈ GMㆍφ이므로 식 (1)은 식 (2)가 된다.

이 경우 식 (2)의 해인 φ의 응답은

가 된다. 여기서 φ₀와 φ₀′는 초기 경사각과 초기 각속도이고 각속도 ω는

를 나타낸다. 또한, ω_n과 ζ는 각각 식 (2)의 고유각속도와 감쇠율(Damping ratio)이다. 한편, 무게중심 G로부터의 선체 횡운동 회전반경(Rolling radius of gyration)을 κ라 하면 횡 관성모멘트 J는

의 관계이므로 식 (2)와 식 (5)로부터 ω_n과 ζ는 다음과 같아진다.

한편, κ를 선체 폭 B와의 비인 계수 C_B에 의해 나타내면

가 된다. 식 (8)의 C_B 값으로는 대략 0.4가 통용될 수 있으며[4]-[6] 혹은 IMO Res. A. 749의 기준에 따라 선체 수선길이 및 흘수가 L 및 d일 때 다음 값으로 정해진다[7].

2.2 진폭감쇠비와 횡감쇠계수의 관계

식 (2)의 J 값은 식 (5)와 식 (8) 또는 식 (9)에 의해 정해질 수 있다. 한편, 횡감쇠계수 식 (2)의 b는 자유 횡요 시 발생하는 맥동현상의 감쇠효과와 관련된 것이므로 이를 시각적으로 확인할 수 있는 자유 횡요 시의 선체 횡진폭감쇠비에 의해 간접적으로 나타내는 것이 가능하다.

여기서 식 (3)의 φ가 최대 혹은 최소가 되는 시점이 순서적으로 t₀, t₁, t₂, ㆍㆍ 일 때 n번째 시점은 t_n이 되고 φ의 진폭감쇠비(Decay ratio)를 λ라 하면 다음 관계가 된다.

또한, t_n일 때 식 (3)의 미분함수는 식 (11)의 조건이 되어야 한다.

이로부터 식 (10), 식 (11)에 의해 λ를 나타내면 다음 식이 얻어진다.

따라서 감쇠계수 b는 λ가 포함되는 식 (13)의 함수로 나타낼 수 있다.

위 식에 식 (6), 식 (7)의 ω_n, ζ를 대입하여 b의 2차식으로부터 감쇠계수 b를 정리하면 다음 식이 된다.

3.1 저속 전복 시의 선체운동

저속으로 전복되는 경우 선체 경사각은 급격한 변화 없이 거의 일정 속도로 완만히 증가하는 형태가 되므로 식 (1)의 J에 의한 각가속도 항이 갖는 크기는 매우 작아져서 이를 무시하면 GZ(φ)는 식 (1)로부터 근사적으로 다음과 같아진다.

경사속도 $$ \stackrel{\text{̇}}{\varphi }$$가 φ₁과 φ₂ 구간에서 일정값 Ω_C이라면 선체의 GZ 크기는 이 구간에서 φ의 함수가 아닌 일정값의 GZ_C가 되므로 식 (15)는 식 (16)으로 표현될 수 있다.

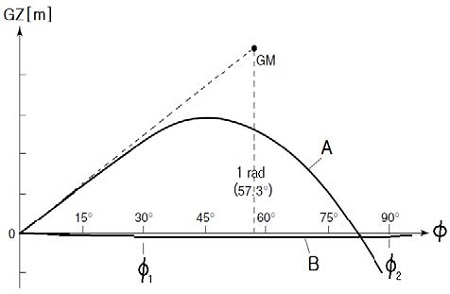
저속전복 시 GZ가 이와 같이 φ와 무관한 일정값으로 취급이 될 수 있다는 것은 복원성이 정상일 때와는 크게 대비가 되는 점이다. 복원성이 정상일 때의 GZ는 식 (2)에서와 같이 φ에 비례하거나 대각도 영역인 경우에도 GZ는 φ에 따라 큰 영향을 받는다는 차이가 있다. 식 (16)이 의미하는 특성은 정복원력 GZ-φ 다이어그램인 Figure 2에서 곡선 B에 의해 설명될 수 있다.

Figure 2:

GZ-φ diagram to describe GZ at slow sinking condition

Figure 2에서 곡선 A는 복원성이 정상일 때의 것으로 GZ는 경사각에 매우 종속적이어서 φ에 따라 양의 방향으로 큰 변화를 보이는 반면 저속전복 상태의 곡선 B에서는 GZ값은 상대적으로 가로축에 매우 접근하는 평탄한 모양이 되고 전복 속도가 느릴수록 음의 방향으로 GZ 크기는 비례적으로 더욱 작아지게 된다. 따라서 곡선 B가 수평인 φ₁ 부터 φ₂ 사이에 해당하는 GZ 값을 GZ_C라 하면 이 구간에서 운동식은 식 (2) 대신 식 (17)이 적용된다.

위 식의 해를 구하면 J = ∆×κ²이므로

이 되고 여기에서 φ₀와 φ₀′는 초기 경사각과 각속도이며 t의 계수인 K_C는

를 나타낸다. 또한, 식 (8)과 식 (11)로부터 K_C는 앞에서의 Ω_C에 해당한다는 것을 알 수 있다.

3.2 전복속도와 GZ값의 관계

선체 상태가 정상적이면 GZ가 양으로 작용하므로 이때의 자유 횡운동은 식 (2)가 적용되지만 이에 대해 화물 선적 등의 잘못으로 복원성이 불량하여 저속 전복 상태가 되면 동일 선박이라도 선체 횡운동은 식 (17)을 따르게 된다. 이로부터 식 (2)에서의 J와 식 (17)에서의 J 값은 서로 같아지고 마찬가지로 양쪽 식에서의 감쇠계수 b 또한 동일한 값으로 작용하므로 식 (2)를 근거로 도출한 식 (14)의 횡감쇠계수 b는 식 (17)의 계수 b로도 그대로 적용하는 것이 가능해진다. 따라서 식 (14)의 감쇠계수를 식 (16)에 대입하면 선체의 전복속도와 GZ 관계는 다음 식으로 얻어진다.

복원성이 양호할 때의 어느 선박이 GM 및 횡요 진폭감쇠비가 λ로 확인된 적이 있다면 이후 해당 선박이 화물 적재 등의 이상으로 인해 외관 상 선체가 Ω_C의 속도로 저속 전복되는 상황이 발생하는 경우 선체에 작용하는 음 방향의 GZ 크기는 식 (20)을 통해 구하는 것이 가능해진다. 즉, 저속전복 사고 시 해당 선박이 정상 복원성인 때 나타내었던 GM과 λ과 같은 과거의 자료가 있다면 식 (20)에 의해서 전복속도와 GZ 간의 비례계수가 계산될 수 있다는 것을 보여준다.

4.1 적용 선박의 제원

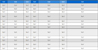
제시된 수식적 관계를 시운전 자료가 Table 1과 같은 선박에 적용하여 결과를 확인해 보기로 한다.

Table 1:

Basic particulars of the model ship

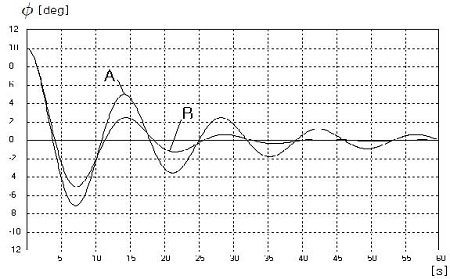
적용선박의 L, B, d가 Table 1에서 128m, 22.4m, 9.5m이므로 이를 식 (9)에 대입하면 C_B는 0.4보다 조금 작은 0.372로 계산된다. 한편, 진폭감쇠비 λ의 설정으로 식 (14)에 의해 횡감쇠계수가 정해지므로 이때의 횡감쇠계수 결과를 식 (2)에 대입하면 횡경사각 φ의 시간 응답은 Figure 3과 같아진다. 여기서 곡선 A, B는 각각 λ = 1/2과 λ = 1/4일 때의 것으로 진폭 감소가 매주기마다 각각 1/2 및 1/4로 나타난다는 것을 확인할 수 있다. 또한, 감쇠가 크게 작용하는 λ = 1/4인 때의 파형 주기는 조금 더 커지는 것으로 나타난다. Figure 3의 결과는 주어진 어느 선박에서 진폭감쇠비의 설정을 토대로 제시된 수식들에 의해 해당 선박의 횡운동 구현에 필요한 계수들이 해석적으로 정해질 수 있음을 보여준다.

Figure 3:

Comparison of damped oscillation curves at λ values of 0.5 and 0.25

4.2 전복속도와 GZ의 관계

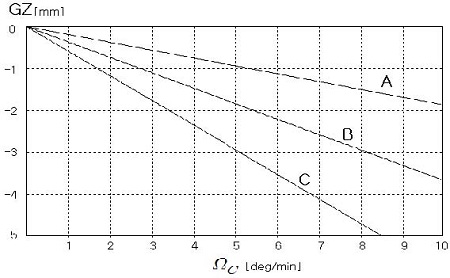
Figure 4는 식 (20)에 의한 전복속도 Ω_C와 이에 해당하는 GZ의 관계를 나타낸 것으로 곡선 A, B, C는 각각 진폭감쇠비 λ가 0.5, 0.25, 0.1일 때의 변화이다.

Figure 4:

Variation of GZ according to observed capsizing speed ΩC at different λ values

가로축의 Ω_C는 rad/s 대신 deg/min의 단위이고 0에서 10deg/min 까지의 범위로 나타내었다. 여기서 Ω_C가 0일 때 GZ는 0이므로 선체는 중립평형 상태가 되어 임의 경사각에서 선체는 정지된다. 한편, 횡감쇠가 작은 곡선 A의 경우는 10deg/min의 비교적 빠른 전복속도에 있을 때에도 음방향의 GZ 크기는 2mm를 넘지 않음을 보여준다. 이로부터 Figure 4의 곡선에 의해 전복 사고 시 경사가 진행되는 속도가 관찰되는 경우 전복되고 있는 선체의 GZ 크기를 구하는 것이 가능해진다는 것을 알 수 있다.

4.3 전복속도와 진폭감쇠비의 관계

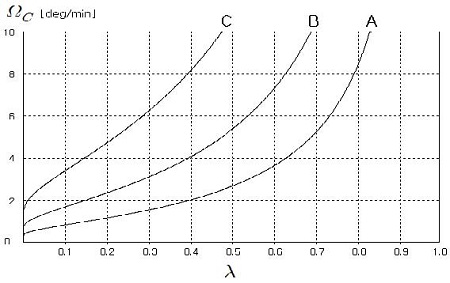
Figure 5는 식 (20)으로부터 진폭감쇠비 λ가 전복속도 Ω_C에 미치는 영향을 나타내기 위한 것이다. 곡선 A, B, C는 각각 GZ가 -0.5mm, -1.0mm, -2.0mm의 일정값으로 작용할 때의 저속전복 상황을 보여준다.

Figure 5:

Variation of leaning speed according to decay ratio λ at different GZ values

GZ가 0.5mm로 크기가 작은 때인 곡선 A의 경우는 λ의 전체 범위에서 λ 변화에 대한 경사속도 Ω_C의 변화가 상대적으로 더 작아진다는 것을 나타내고 있으며 반대로 GZ가 가장 큰 곡선 C일 때 Ω_C는 가장 크게 영향을 받는다는 것을 알 수 있다.