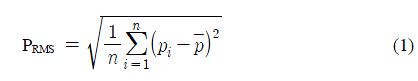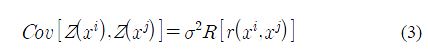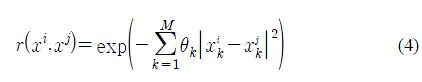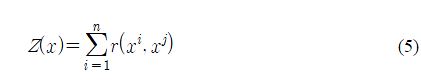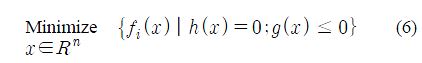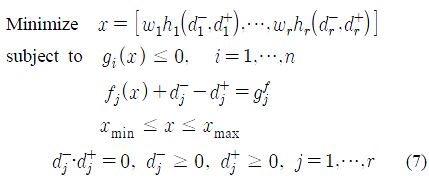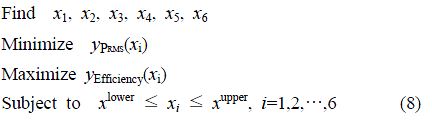Multiobjective optimization strategy based on kriging metamodel and its application to design of axial piston pumps
In this paper, a Kriging metamodel-based multi-objective optimization strategy in conjunction with an NSGA-II(non-dominated sorted genetic algorithm-II) has been employed to optimize the valve-plate shape of the axial piston pump utilizing 3D CFD simulations. The optimization process for minium pressure ripple and maximum pump efficiency is composed of two steps; (1) CFD simulation of the piston pump operation with various combination of six parameters selected based on the optimization principle, and (2) applying a multi-objective optimization approach based on the NSGA-II using the CFD data set to evaluate the Pareto front. Our exploration shows that we can choose an optimal trade-off solution combination to reach a target efficiency of the axial piston pump with minimum pressure ripple.
초록
NSGA-II와 함께 크리깅 메타모델기반 다목적최적설계 전략을 3차원 CFD 시뮬레이션을 통해 액셜 피스톤 펌프의 밸브 플레이트 형상을 최적화하는데 적용하였다. 펌프의 압력 변동을 저감하고 수력 효율을 최대화하기 위한 최적설계 과정은 두 단계, 즉 (1) 밸브 플레이트 상의 6개 형상 설계 변수를 선정하고 각 설계변수의 변화에 따른 CFD 해석을 수행하며, (2) CFD 데이터를 이용한 NSGA-II에 기반한 다목적최적설계 접근방식으로 최소 맥동 압력과 펌프 효율 설계에 대해 파레토 프론트를 평가하는 것으로 구성된다. 이들 결과로부터 최소 맥동 압력을 가지며 액셜 피스톤 펌프의 목표 효율에 도달하는 최적 절충해를 선택할 수 있었다.
Keywords:
Axial piston pump, Discharge pressure ripple, Computational fluid dynamics, Multi-objective optimization, Kriging metamodel, 액셜 피스톤 펌프, 토출압 맥동, 전산유체역학, 다목적최적설계, 크리깅 메타모델1. 서 론
펌프는 유체 수송 시스템의 모든 종류에 사용되는 중요한 구성요소이다. 대부분의 펌프는 두 범주, 즉 용적형 펌프(positive displacement pumps)와 회전동력 펌프(rotordynamic pumps)로 분류된다[1]. 본 연구는 용적형 펌프의 일종인 사축식 액셜 피스톤 펌프(axial piston pump with bent type)의 유동 및 성능 개선에 목적을 두고 수행되었다.
펌프에 대한 CFD(computational fluid dynamics) 시뮬레이션은 외형적 물리적 복잡성 때문에 다루기 힘들고 막대한 크기의 계산 모델이어서 많은 시간이 요구된다. 액셜 피스톤 펌프는 구조적으로 피스톤 상 하사점 근방에서 맥동 유동이 발생하고, 이로 인하여 압력에 의해 발생하는 힘과 모멘트 불균형으로 펌프 내 소음 및 내구성 저하의 원인이 된다. 특히 사축식 액셜 피스톤 펌프는 실험이 매우 어렵기 때문에 3D CFD 시뮬레이션이 펌프 유동 특성을 얼마나 정확하게 예측할 수 있는가가 중요하다. 이러한 이유로 사축식 액셜 피스폰 펌프 설계와 관련된 보고의 중요한 부분은, 토출압 맥동 (discharge pressure ripple)의 수력학적 특성과 효율을 예측하는 능력이다[1]-[7].
전통적으로 펌프 설계는 넓은 작동 범위의 설계요구사양에 대해 1차원 및 2차원 해석 접근을 이용하였다. 하지만 펌프 내의 특정 영역에서 발생하는 불안정 유동 특성(맥동 압력), 실린더 내부의 캐비테이션(cavitation)과 관련된 펌프의 성능 개선에는 어려움이 있다. 액셜 피스톤 펌프의 성능에 영향을 미치는 설계변수는 두 영역, 즉 실린더 내부 밸브 플레이트(valve-plate)와 노치 형상(notch shape)으로 나눌 수 있다. 액셜 피스톤 펌프는 토출압이 주기적으로 변동하는 비정상 상태이고 맥동 압력과 펌프의 수력학적 효율은 서로 상관관계를 가지고 펌프 성능에 영향을 미친다. 따라서 두 반응 특성에 대한 다목적최적설계(multiobjective optimization)의 접근[8]-[12]이 요구된다.
본 논문은 액셜 피스폰 펌프의 중요한 두 반응 특성인 맥동 압력과 수력학적 효율의 다중목적함수에 대해 2단계 과정, (1) CFD 시뮬레이션의 근사화하기 위한 크리깅 메타모델(Kriging metamodel) 구성 부분과, (2) 다중목적함수의 최적해를 얻기 위해 유전자 알고리듬(genetic algorithm)[13]-[15] 적용 단계로 진행된다. 또한 CFD 시뮬레이션과 연결하는 다목적최적설계 프레임웍은, 액셜 피스톤 펌프의 경우 자동화된 파라메트릭 CAD가 어려우므로 외부 DOE(external design of experiment)를 구성하고 이를 텍스트 파일(또는 python)을 이용해서 최적설계에 사용될 입/출력 데이터를 정의하였다.
본 논문에서는 사축식 액셜 피스톤 펌프의 다목적최적설계에 대해 이 방법의 유효성을 설명하였다.
2. 액셜 피스톤 펌프의 CFD 해석
2.1 해석모델의 설명
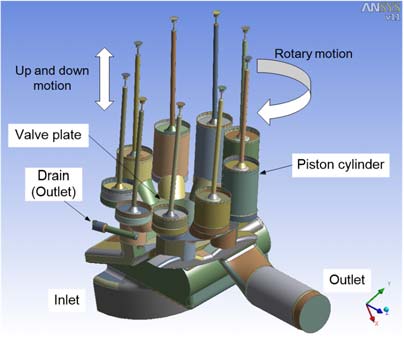
Figure 1은 액셜 피스톤 펌프의 3차원 모델링 결과를 나타낸 것이다. 주요 구성품은 9개의 실린더, 예압축 홀, 노치, 도관부(drain hole), 흡입부 및 도출부로 구성된다.
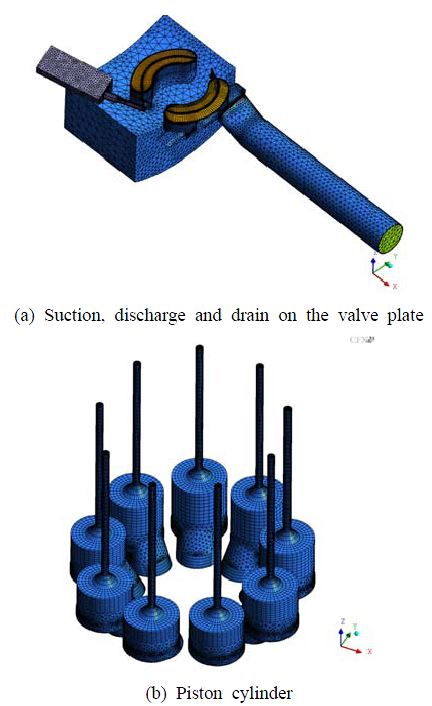
Figure 2는 유동해석을 위한 계산 격자계의 주요 부분인 실린더, 흡입, 토출, 도관부를 나타낸 것이다. 격자계는 ANSYS ICEM CFD[16]를 이용하여 육면체, 사면체 및 프리즘 격자 형태를 혼용하여 생성하였다. 계산 격자의 요소수는 약 529,000개 이다. CFD 시뮬레이션은 상용 프로그램인 ANSYS CFX[17]를 이용하였다. CFD 시뮬레이션에 대한 구체적인 경계조건을 포함한 핵심내용을 설명하면 다음과 같다.
· 비정상 압축성 난류 유동을 해석하기 위해 k-ω을 기반으로 한 SST(shear stress transport) 모델을 사용. 대류항은 upwind biased 접근에 기초한 high resolution을 적용
· 펌프의 입구와 출구 영역에는 흡입과 토출기능 모두가 가능한 Opening 경계조건, 입구는 정압력 1bar, 출구에서는 정압력 350bar 적용
· 실린더부 유동장은 흡입과 압축과정을 반복하는 주기적인 체적 변화를 가지므로 CEL(CFX expression language)를 이용하여 격자가 사인(sine)파형으로 이동하도록 설정
· 실린더부의 회전에 의한 밸브 플레이트의 흡입부와 토출부 교차 영역은 ANSYS CFX에서 지원하는 GGI(general grid interface) 인터페이스 기법[17]을 적용
· 작동유체인 오일(Equivis, ZS46)은 고압에서 압축성 성질을 고려하기 위해 참고문헌 [1]에서 적용한 체적탄성계수를 이용한 압력에 따른 밀도 변화의 관계식을 이용
CFD 계산은 2프로세서를 가진 HP 워크스테이션(2.66GHz, 64bit, 16GB RAM)을 이용하여 유동장을 8개로 분할하여 병렬계산 하였고, 9개의 실린더가 1회전하는 데 약 28시간이 소요되었다.
2.2 CFD 시뮬레이션
본 논문의 액셜 피스톤 펌프는 실린더 부 피스톤의 주기적인 직진운동과 실린더의 고속 회전이 동시에 이루어진다. CFD 시뮬레이션 결과와 실험 결과의 비교는 이전 연구인 참고문헌 [1]에 요약되어 있다.
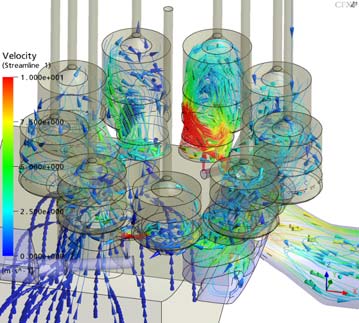
Figure 3은 흡입압력 1bar, 토출압력 350bar, 회전수 1,800 rpm에 대한 유동해석 결과인 실린더 내부 속도분포를 나타낸 것이다. 토출이 시작되는 노치 부근에서 실린더 내부 속도는 약 225 m/s 로 가장 빠르게 계산되었다.
실린더가 흡입부에서 오일을 실린더 내로 유입시키고 이것을 토출부로 내보내기 위해 토출부로 연결하는 순간 토출부의 높은 압력이 갑자기 작용함으로써 실린더 내의 압력은 급격히 증가하고 그 관성으로 인해 맥동현상을 일으킨다. 이러한 현상이 심화되면 실린더 내부 벽에 지속적인 손상을 일으키고, 또한 압력저하로 인하여 캐비테이션 현상이 발생되어 펌프의 소음과 진동의 원인이 된다. 따라서 이러한 현상을 감소시키기 위해 일반적으로 노치 또는 예압축 홀을 만들게 되며 이것들의 위치와 크기 형태는 펌프의 효율을 비롯한 전체 성능에 중요한 영향을 미친다.
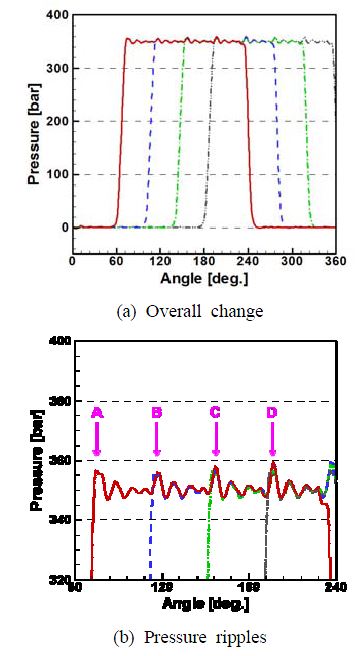
Figure 4 (a)는 9개의 실린더 내부의 한 지점에 대한 압력변화를 나타낸 것이다. 실린더 1개가 토출부에 새로 진입할 때마다 압력 변동 파형이 같은 형태로 주기적으로 나타나고 있다. 밸브 플레이트의 토출 포트에는 항상 4개 정도의 실린더가 연결되어 있으며, 실린더가 토출부를 진입하면서부터 빠져나가는 동안 뒤이어 토출부로 진입하는 실린더에 의하여 압력변화는 4회의 주된 진동을 보인다. Figure 4(b)는 A~D로 확대 표시한 부분으로 유체의 관성 및 압축성 효과로 4회의 주진동과 3회~4회 여기진동 발생을 나타낸 것이다.
실린더가 토출부로 진입한 이후에 발생하는 맥동을 정량화하기 위해, 참고문헌 [1]에 정의한 바와 같이 B~D 구간(SeeFigure 4) 에서 압력 변동의 RMS(root mean square) 값 PRMS를 구하였다.
여기서 Pi는 데이터 채취 시점 ti에서의 압력, n은 데이터 개수를 의미한다. Figure 4의 CFD결과로부터 현재 모델에 대한 액셜 피스톤 펌프의 맥동 압력 PRMS와 효율은 각각 2.53bar, 88.3% 이다.
3. 다목적최적설계 전략
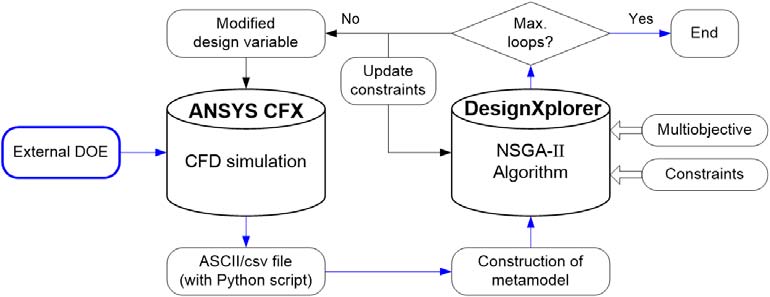
Figure 5는 액셜 피스톤 펌프의 맥동 저감 및 효율 향상을 위한 다목적최적설계 프레임웍을 나타낸 것이다. 액셜 피스톤 펌프의 복잡한 내부 유동장 형상은 최적설계를 위한 자동화된 파라메트릭 CAD 작업이 어렵다. 따라서 CFD 해석 모듈과 최적설계 모듈을 연결하기 전에 독립적으로 외부 DOE를 구성하고 이를 간단한 텍스트 파일 형태인 csv 파일 또는 Python을 이용해 최적설계에 사용될 입/출력 데이터들을 정의하고자 한다. 이 접근은 자동화된 파라메트릭 CAD가 어렵고 소프트웨어의 소스코드가 있는 경우와 없는 경우 모두 사용될 수 있는 유연한 방법이다. 외부 DOE는 두 가지 주요 과정 (1) CFD 데이터로부터 설계변수와 반응값에 대한 함수를 근사적으로 구하기 위한 크리깅 메타모델(Kriging metamodel) 구성 부분과, (2) 구성된 메타모델을 이용하여 다중목적함수의 최적해를 얻기 위한 유전자 알고리듬 적용 단계로 진행된다. 메타모델은 CFD 시뮬레이션 결과에 대한 단순한 해석적 모델(cheap-to-compute 모델의 형태)과 관련된 계산 집약적 함수(computation intensive function)[18][19]로 근사되므로 메타모델에 대한 신뢰도 확보가 이루어진다면 유전자 알고리듬을 수행하는 것이 효율적이고 간단하다. 이하의 절은 각 최적설계 단계를 상세히 설명한다.
3.1 크리깅 메타모델
근사모델(또는 대리모델)에 대한 두 가지 접근법에는 임의의 응답(본 논문에서는 펌프에 대한 결과)에 대해 미분값을 이용하는 테일러 급수(Taylor series) 전개와 적분법을 이용하는 다항식(polynomial function)이 있다. 다항식 전개에 비해 테일러 전개 형태의 근사모델은 설계변수의 범위와 응답의 변동이 작은 경우에 대해서만 적합하다. 보간적 방법으로 생성되는 크리깅 메타모델은 비선형성을 잘 나타낼 수 있는 것으로 알려져 있다. 크리깅 메타모델은 아래 식과 같이 가정한다.
여기서 f(x)는 임의의 설계변수 x의 다항식 함수이다. Z(x)는 평균이 0, 분산이 σ2, 0이 아닌 공분산(non-zero covariance)을 가진 정규분포를 나타내는 가우시안 확률 과정(Gaussian random process)이다. f(x)항은 반응표면(response surface)의 다항식 모델과 비슷하고, 전역적인(globally) 설계공간을 근사한다. 이에 반해, Z(x)는 크리깅 메타모델이 n개의 샘플점으로 이루어진 설계공간을 보간하도록 국부적인(localized) 편차를 생성한다. Z(x)의 공분산 행렬은 식 (3)과 같이 주어진다.
여기서 R은 상관행렬로서 n×n 대칭인 대각선을 따르는 양으로 정의된다. r(xi,xj)은 두 샘플 점 xi와 xj 사이의 공간적 상관관계로서 아래와 같은 형태의 가우시안 상관함수이다.
여기서 M은 설계변수의 수, θk는 모델 적합(curve fitting)에 사용되는 미지의 매개변수, xik와 xjk는 k번째 파라미터의 샘플점 xi와 xj를 나타낸다. 경우에 따라서는, 단일 상관매개변수만으로도 충분히 좋은 결과를 얻을 수 있다. 일반적으로 단일 상관매개변수 또는 각 설계변수에 해당하는 상관매개변수를 사용할 수 있다. Z(x)는 아래의 식 (5)로 나타낸다.
3.2 목표계획법기반 다목적최적설계
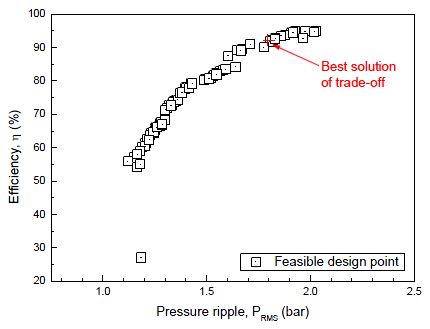
액셜 피스톤 펌프의 최적화는 맥동 압력과 수력학적 효율의 두 가지 목적함수를 가지며 모든 목적함수를 동시에 최소화(또는 최대화)하는 해는 존재하지 않는다. 어떤 목적함수를 개선하기 위해서는 다른 목적함수의 희생이 필요하다. 따라서 각 목적함수 사이에 절충해(trade-off solution) [9][20]를 구하는 것이 바람직하다. 이를 위해 최선해(best solution)로 최소한 하나의 목적함수를 항상 만족하는 최적해들 중의 하나를 선택하는 파레토 해(Pareto solution)나 비지배 집합(non-dominated set)이 자주 사용된다[21]. 일반적인 다중목적함수문제에 대한 최적설계 정식화는 다음과 같이 표현될 수 있다.
여기서 x는 n개의 설계변수 벡터, fi는 i번째 목적함수, h와 g는 등제한 및 부등제한조건 벡터이다. x = { x ∈ Rn : h(x) = 0;g(x) ≤ 0}이면 유용영역이다. 식 (6)을 만족하는 모든 목적함수에 대한 최적해 x* ∈ R는 없으므로 다중목적함수문제는 설계자의 선호(preference)[22][23]에 기반한 목적함수 중요도 크기 f* = (f*1, ···,f*k) 를 결정하고 이를 최선해를 얻는 과정에 반영한다.
본 연구에서는 목표계획법(goal programming)으로 다중목적함수 문제를 해결하고자 한다. 목표계획법은 목적함수가 달성해야 할 목표를 설계자가 결정하고 이를 목표 제한조건(goal constraint)으로 구성하며 실제 제한조건(real constraint)과 함께 최적화를 수행한다. 즉 목적함수가 목표를 달성할 때에는 절충을 고려하고 원래의 제한조건에 대해서는 절충 없이 반드시 만족시키도록 한다. 이를 절충의사결정문제(compromise decision support problem)라 부르고 r개의 다중목적함수는 다음과 같이 정식화 된다[10][24].
여기서 wr는 목적함수의 중요도에 따른 우선순위 가중치, gfj는 목적함수가 달성해야 하는 목표값이다. 그리고 dj-, dj+는 설정목표 달성 시 발생하는 편차(deviation)이며 dj-는 목표 미달량을 dj+는 목표 초과량을 의미한다. 결국 이러한 편차를 최소화함으로써 목표를 최대한 달성시킬 수 있다. 본 논문에서 편차 최소화 방법으로서는 벌칙함수(penalty function), 라그랑지 승수(Lagrange multiplier)가 필요하지 않는 가장 널리 알려진 우수해를 강조하는 엘리티즘 개념(elitism concept)에 기반한 NSGA-II(non-dominated sorted genetic algorithm-II)를 이용하였다[13][25].
4. 최적설계 결과 및 요약
4.1 설계변수와 전산실험계획
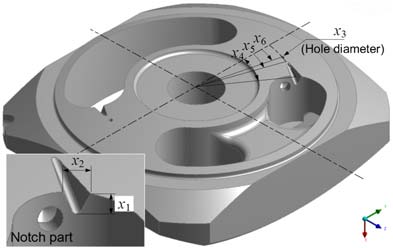
Figure 6은 사축식 액셜 피스톤 펌프에서 진동과 소음에 가장 영향을 미치는 것으로 알려진 밸브 플레이트에 대한 설계변수를 나타낸 것이다. 노치 형상(깊이와 폭)과 관련된 설계변수는 x1, x2, 예압축 홀 지름 및 위치와 관련된 설계변수는 x3, x6, 예압축 홀에서 노치 길이와 관련된 설계변수는 x4, x5, 이다. 밸브 플레이트의 6개 설계변수 범위는 초기모델에 대해 하한 수준 및 상한 수준을 각각 15% 변화시켜 결정하였다.
Table 1은 설계변수와 그 수준 범위를 나타낸 것이다. 현실적으로 액셜 피스톤 펌프는 유동장 생성에 많은 인터페이스 영역과 피쳐(feature), 제약조건(constraint)이 있어 최적설계를 위한 자동화된 파라메트릭 CAD가 어렵다. 따라서 설계공간 내에 전산실험의 회수가 많지 않고 근사모델의 정확도를 높일 수 있는 외부 DOE가 필요하다. 본 논문은 설계변수 개수를 고려하고 비선형성을 잘 표현할 수 있는 자유도가 높은 5수준 직교배열표(orthogonal array)를 사용하여 다목적최적설계를 위한 입출력 설계 데이터로 이용하였다.
Table 2는 선택한 6개 설계변수에 대한 L25(56)직교배열표의 실험배치(design matrix)와 3D CFD 결과를 나타낸 것이다.
4.2 다목적최적설계문제의 정식화
액셜 피스톤 펌프의 가장 중요한 설계요구사항은 맥동현상을 줄이는 것이다. 맥동현상의 개선은 펌프 내 효율의 저하를 가져올 수 있으므로 서로 상충되는 목적이다. 이러한 경우 최적의 유일해를 얻는 것은 불가능하고, 두 목적함수를 동시에 고려하여 상반관계를 고려한 설계 결정이 필요하다.
본 논문에서는 기존 설계의 액셜 피스톤 펌프의 성능에 대한 설계 마진(margin)을 검토하고, 두 목적함수의 균형된 설계점을 찾기 위해 펌프 효율을 최대한 만족시키면서 맥동 압력을 최소화하는 다목적최적설계 문제로 아래의 식 (8)과 같이 정식화하였다.
여기서 y(xi)는 맥동 압력과 효율의 응답에 대한 크리깅 메타모델이다. 효율 yefficiency(xi)는 목표 제한조건으로 설정하고 9개의 실린더가 1회전 후의 유량과 토크 데이터를 추출하고 평균하여 계산하였다.
DOE 결과로부터 다목적최적설계를 위한 근사모델의 생성은 아래 과정을 통해 수행하였다.
[STEP1] L25(56)의 DOE에 대해 CFX를 이용한 CFD 전산실험 데이터 생성
[STEP2] 유연한 파일 인터페이스를 위해 각 스크립트 요소(Excel, Python script 등)에 설계변수와 반응값 도출
Trade-off analysis for Pareto solutions. Note that square-marked ones (with red regression) are designs in the Pareto set with respect to all two objectives
[STEP3] 다항식 기반 민감도 해석 및 크리깅 메타모델의 생성 및 검증
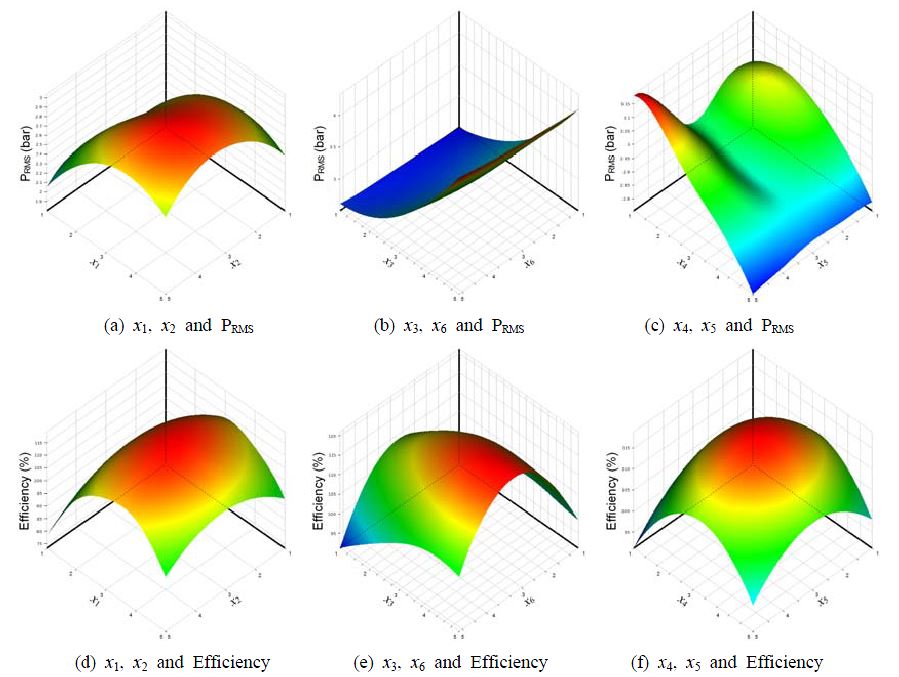
Figure 7은 직교배열표를 통해 얻은 CFD 결과로부터 크리깅 메타모델을 생성하고 이를 바탕으로 각 목적함수의 반응표면분포를 나타낸 것이다. 크리깅 메타모델에서 전역모델은 상수를 사용하였고 전역모델로부터 편차를 표현하는 상관함수는 가우시안 함수를 사용하였다. 두 설계변수의 연결성이 있는 조합에 대해 맥동은 효율보다 비선형성이 강하다. 효율은 최대값을 가지는 전형적인 오목함수(concave function) 형태이고 맥동은 예압축 홀과 위치(x3, x6)의 조합에서 선형성을 노치 길이(x4, x5)에 강한 비선형성이 나타나고 있다. Table 3은 메타모델에 대한 정확도를 평가한 것이다. 임의의 추가 설계점에 대해 크리깅 메타모델은 수정결정계수(adjusted coefficient of determination: best value=1), RMSE(root mean square error: best value=0), RMAE(relative maximum absolute error: best value =0%)[18][19][26]이 모두 좋은 근사품질을 나타낸다.
4.3 파레토 최적해의 결과
다목적최적설계는 파레토 최적해라고 부르는 모든 목적함수들이 서로 지배되지 않는 비지배 해(non-dominated solution)를 이용한다. 그 이유는 어떤 목적함수의 최적해에 대해 다른 목적함수와 비교해서 상대적으로 나은 절충점을 고려할 수 있기 때문이다.
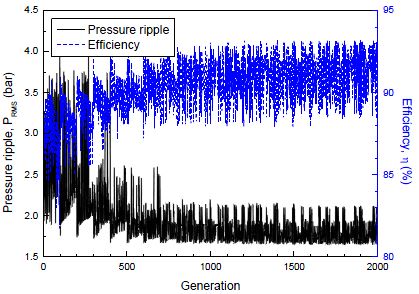
Figure 8은 크리깅 메타모델과 NSGA-II 알고리듬을 이용한 설계변수와 두 목적함수의 상호작용에 의한 파레토 최적해의 수렴 과정을 나타낸 것이다. NSGA II 알고리듬은 상용 최적설계 소프트웨어 ANSYS DesignXplorer 모듈[25]을 이용하였다. NSGA II는 다목적최적설계 분야에 널리 사용되고 있는 비지배 정렬 기반의 유전자 알고리듬으로 개체간의 지배성을 정렬하고 우수해 강조의 방향으로 탐색한다. 개체수(generation) 100개, 1,975 반복 후에 파레토 최적해를 얻었다.
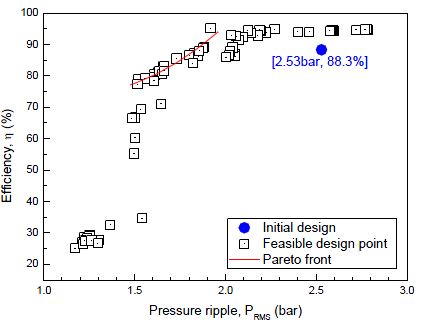
Figure 9는 유용설계공간에 존재하는 파레토 최적해에 대해 두 개의 목적함수의 관계를 나타낸 것이다. 실선은 파레토 최적해의 목적함수들에 의해 형성된 공간인 파레토 프론트(Pareto front)이다. 맥동 압력 2.1bar 이상에서는 효율이 약 90% 정도로 변함이 없다. 따라서 초기 모델의 맥동 압력 2.53bar는 초기 효율을 유지하면서 맥동을 줄일 수 있는 설계공간이 존재한다. 또한 약 2.0bar 이하에서는 맥동 압력과 효율이 절충관계에 있게 되어 효율의 감소 없이는 맥동 압력을 저감시킬 수가 없다. 따라서 효율 90%를 유지하면서 맥동 압력을 최소로 할 수 있는 파레토 프론트 우측 상단의 설계점을 절충점으로 판단하였다. Figure 10은 파레토 프론트 영역에서 다시 우수해의 개체수를 증가시킨 결과를 나타낸 것이다. 효율 90%를 만족시키면서 맥동 압력이 최소화되는 파레토 프론트 영역의 최선해(1.82bar, 91.8%)에서 더 많은 해들이 분포되어 두 목적함수의 상관관계가 더욱 분명하게 나타난다.
Table 4는 파레토 프론트상에서 설계자가 결정한 최적해를 나타낸 것이다. 액셜 피스톤 펌프의 최적모델은 초기모델(맥동 압력 2.53bar, 효율 88.3%)과 비교해서 맥동 압력은 1.83bar로 27.1% 저감되고 최종 모델의 효율은 90.2%로 2.2% 향상되었다. 메타모델로 도출한 최적 파라미터 조건으로 CFD 재해석한 결과와 비교하면, 맥동 압력은 약 0.5%, 효율은 1.7%의 오차가 있다. 이것은 근사모델이 가지는 오차로서, 크리깅 메타모델은 실제의 경향을 잘 나타내고 있다고 말할 수 있다.
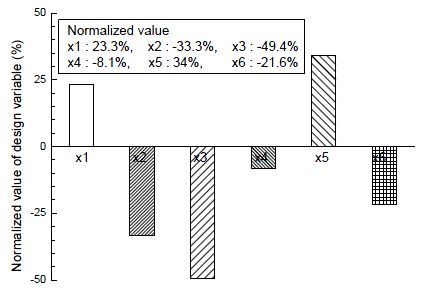
Figure 11은 밸브 플레이트에 대한 정규화된 최적설계변수를 나타낸 것이다. 밸브 플레이트의 다목적 최적해에 대한 설계변수의 변화량은 초기모델에 대해 x1=23.3%, x2=-33.3% x3=-49.4%, x4=-8.1%, x5=34%, x6=-21.6%이다.
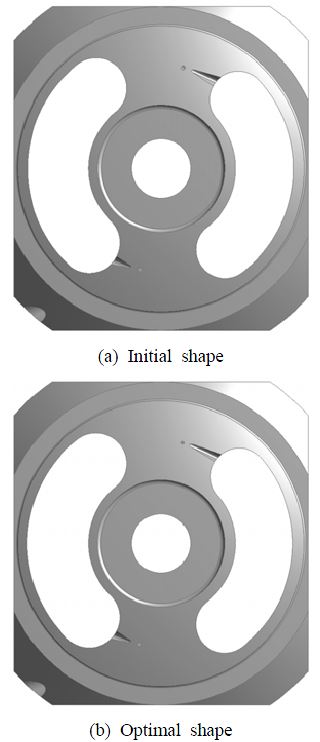
Figure 12는 액셜 피스톤 펌프용 밸브 플레이트의 초기모델과 최적모델의 형상을 나타낸 것이다. 예압축 홀 지름과 노치 면적(길이와 폭, 깊이)이 초기모델에 비해 많이 변화되었음을 알 수 있다 (노치 면적은 해당 기업의 기술적 이유로 설명하지 않음). 오일 홀 지름과 노치 면적 크기를 변화시킴으로써 피스톤의 상 하사점 근방에서 실린더 내의 압력 변동 구배를 완만하게 하고 이것이 맥동 저감과 특정 영역에서 효율 개선을 가져오는 것으로 판단된다.
5. 결 론
3차원 액셜 피스톤 펌프의 최적설계를 위한 메타모델을 구하고 이로부터 다목적최적설계에 필요한 데이터들을 CFD로부터 효과적으로 구하는 방법을 적용하고 펌프의 최적설계를 시도하였다. 3차원 유동 특성을 위한 근사모델은 다항식 및 크리깅 메타모델을 이용하였다. 주요 결과를 요약하면 다음과 같다.
(1) 액셜 피스톤 펌프에 대한 자동화된 CAD가 어려우므로 CFX에 의한 DOE를 구성하여 텍스트 데이터를 얻거나 저급 프로그래밍 언어를 통하여 최적설계에 필요한 데이터를 교환하는 효율적인 다목적최적설계 프레임웍을 제안하고 그 유효성을 검증하였다.
(2) 크리깅 메타모델과 NSGA-II 알고리듬을 이용한 다목적최적설계를 통해 맥동 압력과 펌프 효율의 두 목적함수 사이의 절충을 고려하는 균형된 최적 설계점을 찾았다.
(3) 액셜 피스톤 펌프의 최적모델은 초기모델(맥동 압력 2.53bar, 효율 88.3%)과 비교해서 맥동 압력은 1.83bar로 27.1% 저감되고 효율은 90.2%로 2.2% 향상되었다. 메타모델로 구한 최적해에 대해 CFD 재해석 결과와 비교하면, 맥동 압력은 약 0.5%, 효율은 1.7%의 오차로 크리깅 메타모델은 실제의 경향을 잘 나타내고 있다.
Acknowledgments
이 논문은 2009년도 정부(미래창조과학부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(No. 2009-0083510).
References
-
J. H. Jeong, J. K. Kim, and Y. K. Suh, “Numerical study on hydraulic fluid flows within axial piston pump”, Transactions of The Korean Society of Mechanical Engineers B, 34(2), p129-136, (2010).
[https://doi.org/10.3795/KSME-B.2010.34.2.129]

-
Y. B. Lee, and G. C. Lee, “An experimental study on the improving noise characteristic of hydraulic power unit”, Journal of the Korean Society of Marine Engineering, 37(6), p638-643, (2013).
[https://doi.org/10.5916/jkosme.2013.37.6.638]

-
N. D. Manring, “Valve-plate design for an axial piston pump operating at low displacements”, American Society of Mechanical Engineers Journal of Mechanical Design, 125(1), p200-205, (2003).
[https://doi.org/10.1115/1.1541632]

-
J. Kim, H. Kim, Y. Lee, J. Jung, and S. Oh, “Measurement of fluid film thickness on the valve plate in oil hydraulic axial piston pumps (Part II: Spherical Design Effects)”, Journal of Mechanical Science and Technology, 19(2), p655-663, (2005).
[https://doi.org/10.1007/BF02916187]

-
S. Wang, “The analysis of cavitation problems in the axial piston pump”, American Society of Mechanical Engineers Journal of Fluids Engineering, 132(7), p074502, (2010).
[https://doi.org/10.1115/1.4002058]

-
S. Wang, “Improving the volumetric efficiency of the axial piston pump”, American Society of Mechanical Engineers Journal of Mechanical Design, 134(11), p111001, (2012).
[https://doi.org/10.1115/1.4007361]

- D. H. Jang, S. K. Lee, J. H. Kwon, and S. H. Park, “A study on pressure, flow fluctuation and noise in the cylinder of swash plate type axial piston pump”, Transactions of the Korea fluid power systems society, 6(3), p1-9, (2009).
- R. E. Steuer, Multiple Criteria Optimization:Theory, Computation and Application, John Wiley & Sons, New York, (1986).
- S. H. Baek, S. S. Cho, H. S. Kim, and W. S. Joo, “Trade-off analysis in multi-objective optimization using chebyshev orthogonal polynomials”, Journal of Mechanical Science and Technology, 20(3), p336-375, (2006).
- S. H. Baek, S. S. Cho, and W. S. Joo, “Response surface approximation for fatigue life prediction and its application to multi-criteria optimization with a priori preference information”, Transactions of The Korean Society of Mechanical Engineers A, 33(2), p114-126, (2009).
- X. G. Song, L. Wang, S. H. Baek, and Y. C. Park, “Multidisciplinary optimization of a butbutterfly valve”, International Society of Automation Transactions, 48(3), p370-377, (2009).
-
T. Goel, N. Stander, and Y. Lin, “Efficient resource allocation for genetic algorithm based multi-objective optimization with 1,000 simulations”, Structural and Multidisciplinary Optimization, 41(3), p421-432, (2010).
[https://doi.org/10.1007/s00158-009-0426-9]

- K. Deb, Multi-objective Optimization Using Evolutionary Algorithms, Wiley, New York, (2001).
-
K. Deb, A. Pratap, S. Agarwal, and T. Meyarivan, “A fast and elitist multiobjective genetic algorithm: NSGA-II”, Institute of Electrical and Electronics Engineers on Evolutionary Computation, 6(2), p182-197, (2002).
[https://doi.org/10.1109/4235.996017]

-
I. Ferreira, J. A. Cabral, P. Saraiva, and M. C. Oliveira, “A multidisciplinary framwork to support the design of injection mold tools”, Structural and Multidisciplinary Optimization, 48(220), p1-21, (2013).
[https://doi.org/10.1007/s00158-013-0990-x]

- ANSYS ICEM CFD 10.0 User Guide, (2010).
- ANSYS CFX 10.0 Theory Guide, (2010).
-
S. H. Baek, K. M. Kim, S. S. Cho, D. Y. Jang, and W. S. Joo, “A sequential optimization algorithm using metamodel based smultilevel analysis”, Transactions of The Korean Society of Mechanical Engineers A, 33(9), p892-902, (2009).
[https://doi.org/10.3795/KSME-A.2009.33.9.892]

-
G. G. Wang, and S. Shan, “Review of metamodeling techniques in support of engineering design optimization”, American Society of Mechanical Engineers Journal of Mechanical Design, 129(4), p370-380, (2007).
[https://doi.org/10.1115/1.2429697]

-
E. Acar, R. T. Haftka, and T. F. Johnson, “Tradeoff of uncertainty reduction mechanisms for reducing weight of composite laminates”, American Society of Mechanical Engineers Journal of Mechanical Design, 129(3), p266-274, (2007).
[https://doi.org/10.1115/1.2406097]

-
E. M. Kasprzak, and K. E. Lewis, “Pareto analysis in multiobjective optimization using the collinearity theorem and scaling method”, Structural and Multidisciplinary Optimization, 22(3), p208-211, (2001).
[https://doi.org/10.1007/s001580100138]

-
H. A. Jensen, and A. E. Sepulveda, “A preference aggregation rule approach for structural optimization”, Structural and Multidisciplinary Optimization, 16(4), p246-257, (1998).
[https://doi.org/10.1007/BF01271431]

-
B. J. Hunt, V. Y. Blouin, and M. M. Wiecek, “Modeling relative importance of design criteria with a modified pareto preference”, American Society of Mechanical Engineers Journal of Mechanical Design, 129(9), p907-914, (2007).
[https://doi.org/10.1115/1.2747634]

-
A. Engau, and M. M. Wiecek, “2D decision-making for multicriteria design optimization”, Structural and Multidisciplinary Optimization, 34(4), p301-315, (2007).
[https://doi.org/10.1007/s00158-006-0078-y]

- ANSYS DesignXplorer 14.5 Workbench User Guide, (2012).
-
G. Rennen, “Subset selection from large datasets for kriging modeling”, Structural and Multidisciplinary Optimization, 38(6), p545-569, (2009).
[https://doi.org/10.1007/s00158-008-0306-8]