The Korean Society of Marine Engineering

[ Original Paper ]

Journal of Advanced Marine Engineering and Technology - Vol. 47, No. 5, pp.244-251

ISSN: 2234-7925 (Print) 2765-4796 (Online)

Print publication date 31 Oct 2023

Received 11 Oct 2023 Revised 20 Oct 2023 Accepted 29 Oct 2023

DOI: https://doi.org/10.5916/jamet.2023.47.5.244

Improved sliding mode observer for FOC control system with discontinuous PWM of sensorless PMSM

VU VAN HUNG¹ ; Kyoung-kuk Yoon^†

; Sung-geun Lee^††

1M. S. Candidate, Electrical and Electronics Engineering, Korea Maritime & Ocean University, Tel: 051-410-4891 vuvanhung190199@gmail.com

Correspondence to: ^††Professor, Major of Electrical and Electronics Engineering, Korea Maritime & Ocean University, 727, Taejong-ro, Yeongdo-gu, Busan 49112, Korea, E-mail: sglee48@kmou.ac.kr, Tel: 051-410-4821 Contributed by footnote: ^†Assistant Professor, Maritime AI and Cyber Security, Korea Maritime & Ocean University, 727, Taejong-ro, Yeongdo-gu, Busan 49112, Korea, E-mail: kkyoon@kmou.ac.kr, Tel:051-410-4265

Copyright © The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Abstract

With the increasing number of electric cars worldwide, permanent-magnet synchronous motors (PMSMs) are becoming increasingly popular in the transportation industry. In parallel with the development of PMSM, many novel control strategies have been developed to make PMSM superior and robust. In all control strategies aimed at improving the operation of PMSMs, the control strategy using discontinuous pulse width modulation (DPWM) instead of continuous space vector pulse width modulation (CSVPWM) for field-oriented control (FOC) is widely used to reduce switching and save energy. However, this method has not been applied by researchers to sensorless PMSM control three-phase inverters. Therefore, this study investigated a sensorless PMSM control with a DPWM FOC and a traditional sliding-mode observer to estimate rotor positions. Additionally, a modified sliding-mode observer with a Park phase-locked loop (PLL) was designed experimentally to improve the stability of the PMSM speed and reduce harmonics in the output phase current for the inverter under the FOC with DPWM. The experimental results verified that the sliding-mode observer integrated with the Park PLL can improve the operation of the sensorless PMSMs under FOC with DPWM.

Keywords:

Sensorless PMSM, Discontinuous Pulse Width Modulation (DPWM), Sliding Mode Observer (SMO), Park Phase-Locked Loop (PLL), Field-Oriented Control (FOC)

1. Introduction

Mechanical engines are gradually being replaced by electrical motors because the earth is gradually exhausted of natural resources and fuel. Electrical motors are utilized not only in electrical vehicles but also in factories, enterprises, and construction sites, and have advantages such as compact size, accurate operation, and environmental friendliness compared to mechanical engines with similar power [1].

Among the types of electric motors, DC motors are more efficient, and the control method is simpler than that of AC motors; however, AC motors require less maintenance and can be easily adapted to various circumstances and environmental conditions. Permanent magnet synchronous motors (PMSMs) are a typical type of AC motors. Compared to other motors, PMSMs are widely used in electric vehicles, aerospace applications, and devices that require high accuracy. PMSMs have several advantages because of their special structure. In a PMSM, the rotor is constructed using a series of permanent magnets, and the stator is wound with a copper wire [2]. PMSMs can achieve a low torque ripple coefficient, high power density, and fast dynamic response by using the magnetic flux generated from the permanent magnets [3][4][5]. To make the PMSMs robust and achieve better power performance, many control strategies have been proposed, such as decreasing power loss by using SIC MOSFETs instead of Si IGBTs [6] or performing an improved MPC [7]. Modifying the PWM scheme in FOC is a simple and effective method. Normally, in FOC, continuous space vector PWM (CSVPWM) is stable and creates fewer harmonics than discontinuous PWM (DPWM). However, DPWM can reduce the switching loss for PMSM control three-phase inverters [8][9][10].

In another development field of PMSM, the mechanical position sensor is removed to reduce the cost and size of PMSM. Therefore, sensorless control strategies for PMSM have become an interesting topic. Many superior algorithms for estimating the positions of sensorless PMSMs have been proposed. For example, in [11], an improved sliding-mode observer was proposed by integrating adaptive synchronization and a quadrature phase-lock loop. Additionally, a model reference adaptive system (MRAS) [12] was used to estimate the position from the current and voltage of the PMSM in the dq frame. Other complicated computation methods such as the extended Kalman filter (EKF) [13][14] and Luenburger observer were used [15].

However, the research papers only focus on developing position estimation algorithms for sensorless PMSM and conducting experiments with a continuous space vector PWM based on FOC. Thus, this paper presents a method for estimating the angular position of a motor using a sliding mode observer (SMO) modified to improve efficiency and reduce harmonics for the motor current with a DPWM strategy based on FOC.

2. Mathematical Model of PMSM

Determining a PMSM model is important for precisely and effectively controlling PMSM. The equation of state for PMSMs in the dq frame can be expressed as follows:

d i d d t = 1 L s - R s i d + ω e L s i q + u d d i q d t = 1 L s - R s i q - ω e L s i d - ω e ψ f + u q

(1)

where i_d and i_q are the dq axis stator currents, and u_d and u_q are the dq axis stator voltages. ω_e is the rotor electrical speed, and ψ_f is flux linkage. R_s and L_s are the resistance and inductance of the stator, respectively.

And in αβ stationary reference frame as:

d i α d t = 1 L s - R s i α - e α + u α d i β d t = 1 L s - R s i β - e β + u β

(2)

Here i_α and i_β and u_α and u_β are αβ stationary reference frame currents and voltages, respectively. Additionally, e_α and e_β are αβ frame back electromotive forces (back emf), which are described as

e α = - ψ f ω e s i n θ e β = ψ f ω e c o s θ

(3)

Using Equation (3), the position and speed of PMSM rotors can be calculated as follows:

θ = - a r c t a n e α e β ω e = e α 2 + e β 2 ψ f

(4)

Based on the above equations, the observer and control strategies for PMSMs are discussed and established in the subsequent sections.

3. Field-Oriented Control Strategy for PMSM

3.1 Conventional Field-Oriented Control

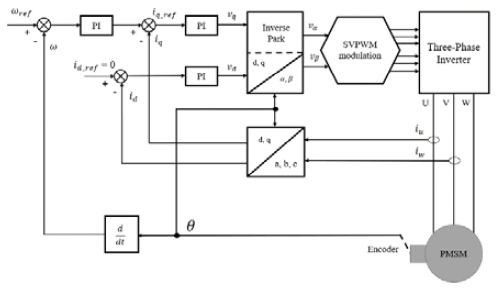
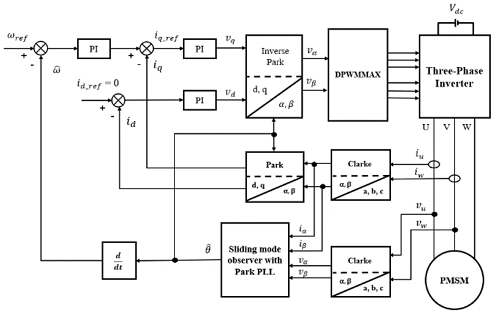
Field-oriented control (FOC) is a well-known method for three-phase motor control. In the three-phase PMSM control with a position sensor, as shown in Figure 1, the position signal of the rotor is used to calculate the speed of the motor and then provide feedback for comparison with the reference speed.

Figure 1:

Field-oriented control block diagram with a sensor PMSM

Normally, the SVPWM block in the FOC operates with continuous space-vector pulse-width modulation (CSVPWM). CSVPWM is shown in Figure 2. CSVPWM has a power loss problem owing to its high switching loss. Hence, discontinuous pulse-width modulation (DPWM) was used instead of CSVPWM. Although DPWM produces more harmonics in the output current than CSVPWM, DPWM can significantly reduce the switching loss of a three-phase inverter. Switching loss is the amount of power loss in semiconductor switches when the inverter operates at a high frequency. This phenomenon cannot be avoided by reducing the size of the device or by reducing harmonics. Therefore, the device must operate under high-frequency conditions.

Figure 2:

Continuous SVPWM

3.2 Discontinuous Pulse-Width Modulation for Field-Oriented Control System

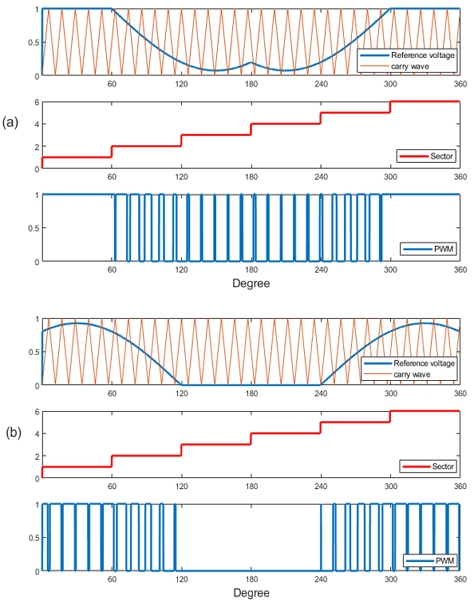
Fundamentally, the DPWM operation for the three-phase inverter control of PMSMs is the creation of either one of two ineffective voltage vectors, namely, the zero vector or the seventh ineffective voltage vector within a single switching cycle. This is in contrast to CSVPWM, which generates both ineffective voltage vectors during each switching cycle. With this strategy, the control system can reduce the ineffective voltage vectors and the number of switchings. The two typical variants of DPWM in the PMSM-controlled three-phase inverter introduced in this study are DPWMMIN and DPWMMAX. Graphical representations of the DPWMMIN and DPWMMAX waveforms are shown in Figure 3.

Figure 3:

DPWM: (a) DPWMMAX and (b) DPWMMIN

In 60-degree discontinuous modulation, if the zero-ineffective voltage vector is generated across all six sectors and the reference voltage is clamped at the lower part of the DC bus, this type is called DPWMMIN. Conversely, when only the seventh ineffective voltage vector is created and the reference voltage is clamped on the upper DC bus, it is called DPWMMAX. Because of the clamping to the lower or upper DC bus, the output voltage of each phase is clamped at zero of the DC bus sequentially for DPWMMIN and clamped at the maximum of the DC bus for DPWMMAX. During the clamped output voltage period, the switches at each phase remain in turn-on or turn-off status. As a result, the switching loss is reduced by the DPWM [16][17].

4. Design of Sliding Mode Observer for Sensorless PMSM Controlled with DPWM

4.1 Conventional Sliding Mode Observer

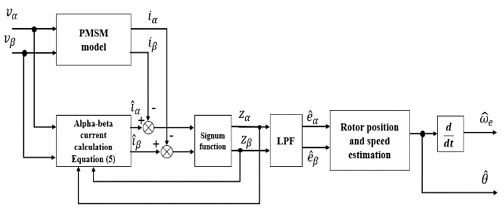
A conventional sliding mode observer (SMO) was established using the αβ stationary reference frame voltage equation to observe rotor position and estimate the speed of sensorless PMSM based on back electromotive force (back emf). Figure 4 shows a conventional sliding mode observer diagram with the rotor position and speed in the output.

Figure 4:

Conventional sliding mode observer diagram

In the sliding mode observer, back emf was obtained from the difference between the estimated αβ currents and real measured currents of the motor with signum function and low pass filter. The real measured currents are i_α and i_β and the real measured voltages are v_α and v_β. The estimated αβ currents were calculated using Equation (5).

d ı^α d t = - 1 L s R s ı^α - v α + K s i g n ı^α - i α d ı^β d t = - 1 L s R s ı^β - v β + K s i g n ı^β - i β

(5)

where K is the gain of the observer and is multiplied by the sign function. K gain must be sufficiently large and satisfy the condition of K > max(|e_α||e_β|). And back emf is as Equation (6).

z α = K s i g n l^α - i α z β = K s i g n l^β - i β

(6)

Because z_α and z_β include a large number of interferences to achieve accurate back emf (e_α and e_β), using low pass filter (LPF) for the value of z_α and z_β is necessary.

e^α = w c τ + w c z α e^β = w c τ + w c z β

(7)

where w_c is the cut-off frequency and τ is the time constant of LPF. Thus, based on Equation (4), the position and speed of the rotor can be estimated using Equations (8) and (9).

θ^= - a r c t a n e^α e^β

(8)

ω^e = d d t θ^

(9)

Using a conventional sliding-mode observer, an experiment was conducted to evaluate the observer’s ability, and the results are presented in the experimental section.

4.2 Integrating Sliding Mode Observer with Park Phase-Locked Loop

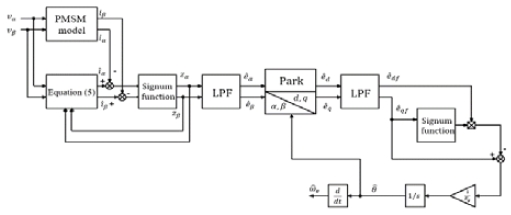
Conventional sliding-mode observers have some weaknesses in that they cannot completely attenuate the interference and chatter in the estimated position signal. Because of the disturbance that appears in the estimated position signal, the output current can also be affected and distorted. Therefore, this study proposed an improved sliding-mode observer with a Park-phase-locked loop. In the proposed method, the estimated αβ frame back emf is exchanged to the dq frame. By exchanging the dq frame, the dq frame back EMF signal had two direct lines; therefore, it was more effective when implementing two filters in the output. Hence, the output signal was attenuated by interference and chattering. A block diagram of the sliding-mode observer with a Park phase-locked loop is shown in Figure 5.

Figure 5:

Improved sliding mode observer with a Park phase-locked loop block diagram

As illustrated in the block diagram, the Park block converted the αβ frame back emf to dq frame back emf. The conversion was implemented using Equation (10).

e^d e^q = s i n θ^c o s θ^- c o s θ^s i n θ^e^a e^β

(10)

After the conversion process, the values of the returned emf and dq components were filtered through a first-order filter. Here, the first-order filter was a low-pass filter.

e^d f e^q f = w c 2 τ + w c 2 e^d e^q

(11)

where w_c₂ is cut-off frequency and different from the cutoff frequency in Equation (7). The rotor position was obtained using Equation (12).

θ^= ∫ 1 K g e^q f - s i g n e^q f ⋅ e^d f

(12)

In the above equation, K_g is the voltage gain, and the sign is the signum function. The speed was obtained easily by deriving the estimated rotor position.

ω^e = d d t θ^

(13)

With an additional Park PLL at the output of the SMO, the interference and chattering of the estimated rotor-position signal were significantly reduced. Hence, the output current in the inverter phases were more stable and the harmonics were reduced. The results of this method are compared with those of the conventional SMO in the experimental results section.

5. Experiment and Results

5.1 Experiment Configuration

Figure 6 shows a block diagram of the Sensorless PMSM control method. The control method was field-oriented with a modified sliding-mode observer to respond to speed and position feedback. The DPWMMAX strategy was utilized in the SVPWM block, and the parameters of the PMSM used to compute the SMO are listed in Table 1.

Figure 6:

Control strategy block diagram

Table 1:

Parameters of PMSM used in the experiment

The experimental setup for the sensorless PMSM is shown in Figure 7. The system used a three-phase variable DC power supply to provide a 24 V DC input to the inverter. The 24 V DC input was converted to a three-phase AC voltage for application to the PMSM. In the DC-to-AC converter board, six IGBTs were controlled in the gate terminal by a switching pulse. Switching pulses were generated using a DSP TMS320F28335D on the control board. The DSP TMS320F28335D also implemented the proposed algorithm and received an analog feedback signal from the sensors on the control board. The experimental data were saved and plotted in MATLAB using a JTAG emulator (XDS 300S) of Syncworks, and the current waveform and switching pulse were measured using a digital oscilloscope.

Figure 7:

Experimental setup

5.2 Results of the Experiment

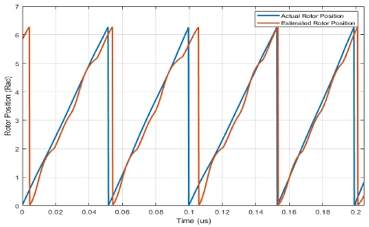
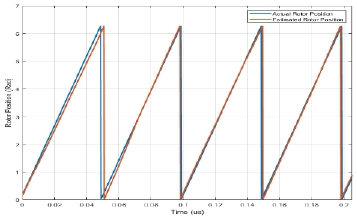
A. Conventional Sliding Mode Observer

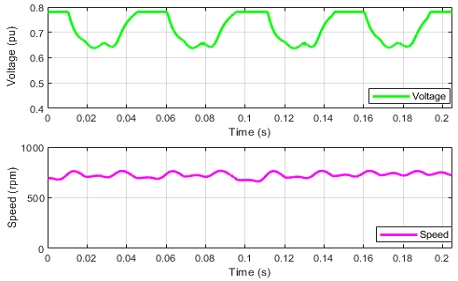
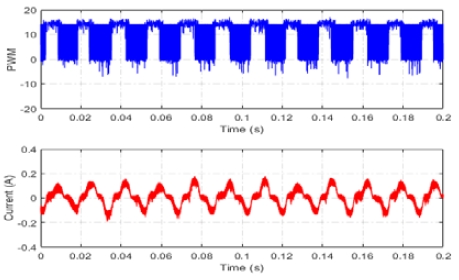
Figure 8 shows the rotor position estimated using a conventional sliding-mode observer and the actual rotor position measured using a mechanical encoder integrated with the PMSM. Using Figure 8 as a reference, it can be observed that the estimated rotor position closely approximated the rotor-position determined by the encoder. However, the estimated signal exhibited discernible chatter and lacked clarity. Owing to the presence of noise in the estimated rotor position, the operational performance of the IGBT gate drivers, specifically the speed and reference switching times, was adversely affected. As shown in Figure 9, the motor speed was unstable between 600 and 700 rpm, and the reference phase-voltage waveform became distorted compared with the ideal phase-voltage waveform shown in Figure 3(a). In addition, the inverter operated with the gate-drive switching pulses of the DPWMMAX, and the output phase current is shown in Figure 10.

Figure 8:

Estimated and actual rotor posistions

Figure 9:

Reference phase voltage of DPWM and motor speed

Figure 10:

IGBT gate drive pulse and output phase current

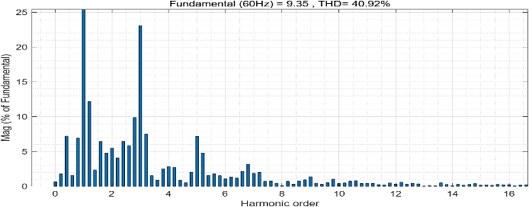
Under the feedback signals of the conventional SMO, the total harmonic distortion of the output phase current was 40.92% at a fundamental frequency of 60 Hz, as shown in Figure 11.

Figure 11:

Output phase current total harmonic distortion

B. Improved Sliding Mode Observer with Park PLL

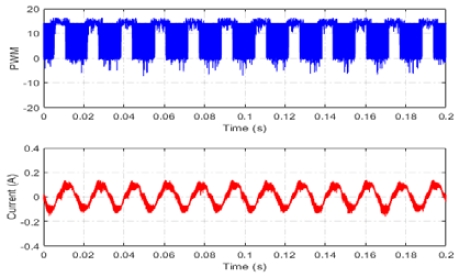
Similar to the conventional sliding-mode observer, Figure 12 shows the estimated rotor position obtained using the sliding-mode observer in conjunction with a Park PLL. This estimated position was closer to the actual rotor position, and the chatter was significantly reduced. Therefore, the speed of the motor was more stable at 700 rpm. The reference phase voltage waveform is as ideal phase voltage waveform in Figure 3(a) as shown in Figure 13, and the phase current waveform was almost sinusoidal, as shown in Figure 14.

Figure 12:

Estimated and actual rotor positions.

Figure 13:

Reference phase voltage of DPWM and motor’s speed

Figure 14:

IGBT gate drive pulse and output phase current

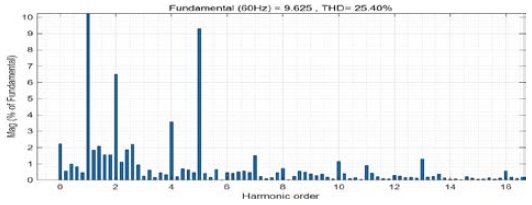
Additionally, the harmonics existing in the current phase were significantly reduced, as indicated by the THD coefficient shown in Figure 15.

Figure 15:

Output phase current total harmonic distortion

In the case of a PMSM operating with an improved sliding-mode observer with a Park PLL, the total harmonic distortion of the output phase current was 25.40% at a fundamental frequency of 60 Hz, as shown in Figure 15.

6. Conclusions

This study proposed an improved sliding mode observer with the Park phase-locked loop algorithm for estimating the rotor position of PMSMs under DPWM FOC.

Under similar conditions and input references between a conventional SMO and the improved sliding mode observer with the Park phase-locked loop, by the improved sliding mode observer the results were obtained :

(1) the position of the rotor was accurately estimated without chatters or interferences;

(2) the output speed of the PMSM was more stable when the reference speed was 700 rpm;

(3) the experimental results show that the harmonics in the current of phases decreased significantly from 40.92% to 25.40% compared to those using a conventional SMO.

Acknowledgments

This work was supported by Advanced Technology Center Plus(ATC+) program funded by the Ministry of Trade, Industry and Energy. [Project Name : The Development for Telescopic Bridge to Maintain of Ocean Structure and Transfer Material with Active Motion Control System , Project Number : 20017957].

Author Contributions

Conceptualization, V. V. HUNG, K. K. Yoon and S. G. Lee; Methodology, V. V. HUNG, K. K. Yoon and S. G. Lee; Software, V. V. HUNG; Formal Analysis, V. V. HUNG and S. G; Investigation, V. V. HUNG and K. K. Yoon; Data curation V. V. HUNG and S. G. Lee; Writing Original Draft Preparation, V. V. HUNG; Writing-Review & Editing, S. G. Lee; Visualization, V. V. HUNG and K. K. Yoon; Supervision, S. G. Lee; Project Administration, K. K. Yoon and S. G. Lee; Funding Acquisition, S. G. Lee.

References

I. Husain, and et al., “Electric drive technology trends, challenges, and opportunities for future electric vehicles.” Proceedings of the IEEE, vol. 109, no. 6, pp. 1039-1059, 2021. [https://doi.org/10.1109/JPROC.2020.3046112]
H. K. Patel, R. Nagarsheth, and S. Parnerkar, “Performance comparison of permanent magnet synchronous motor and induction motor for cooling tower application,” International Journal of Emerging Technology and Advanced Engineering vol. 2, no. 8, pp. 167-171, 2012.
X. Song, J. Fang, and B. Han, “High-precision rotor position detection for high-speed surface PMSM drive based on linear Hall-effect sensors,” IEEE Transactions on Power Electronics vol. 31, no. 7, pp. 4720-4731, 2015. [https://doi.org/10.1109/TPEL.2015.2479642]
J. H. Song and K. -H. Kim, “Reliable open-switch fault localization scheme in multiple switches for inverter-fed permanent magnet synchronous machine drives,” Electric Power Components and Systems, vol. 45, no. 18, pp. 1973-1984, 2017. [https://doi.org/10.1080/15325008.2017.1401685]
K. Jezernik, J. Korelic, and R. Horvat, “PMSM sliding mode FPGA-based control for torque ripple reduction,” IEEE Transactions on Power Electronics, vol. 28, no. 7, pp. 3549-3556, 2013. [https://doi.org/10.1109/TPEL.2012.2222675]
Q. Haihong, and et al., “Comparisons of SiC and Si devices for PMSM drives,” 2016 IEEE 8th International Power Electronics and Motion Control Conference (IPEMC-ECCE Asia), 2016. [https://doi.org/10.1109/IPEMC.2016.7512404]
J. Chen, and et al., “Improved efficiency of a PMSM drive with model predictive control,” 2019 IEEE International Symposium on Predictive Control of Electrical Drives and Power Electronics (PRECEDE), IEEE, 2019. [https://doi.org/10.1109/PRECEDE.2019.8753342]
U. Muduli, B. Chikondra, and R. Behera, “Continuous and discontinuous svpwm with switching loss control for five-phase two-level VSI fed induction motor drive,” 2020 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), IEEE, 2020. [https://doi.org/10.1109/PEDES49360.2020.9379717]
O. Ojo and P. Kshirsagar, “The generalized discontinuous PWM modulation scheme for three-phase voltage source inverters,” IECON'03. 29th Annual Conference of the IEEE Industrial Electronics Society (IEEE Cat. No. 03CH37468), vol. 2, IEEE, 2003.
F. Zaamouche, S. Saad, and L. Hamiche, “A discontinuous PWM techniques evaluation by analysis of voltage and current waveforms,” International Journal of Scientific Engineering and Technology, 2018.
Y. Chen, and et al., “A sliding mode speed and position observer for a surface-mounted PMSM,” ISA transactions, vol. 87, pp. 17-27, 2019. [https://doi.org/10.1016/j.isatra.2018.11.011]
A. Mishra, and et al., “MRAS based estimation of speed in sensorless PMSM drive,” 2012 IEEE Fifth Power India Conference, IEEE, 2012. [https://doi.org/10.1109/PowerI.2012.6479492]
Z. Zheng, Y. Li, and M. Fadel, “Sensorless control of PMSM based on extended kalman filter,” 2007 European Conference on Power Electronics and Applications, IEEE, 2007. [https://doi.org/10.1109/EPE.2007.4417275]
A. Qiu, B. Wu, and H. Kojori, “Sensorless control of permanent magnet synchronous motor using extended Kalman filter,” Canadian Conference on Electrical and Computer Engineering 2004 (IEEE Cat. No. 04CH37513), vol. 3, IEEE, 2004.
Q. Mi and R. Ma, “A novel Luenberger observer for the sensorless speed control of PMSM,” PCIM Asia 2021; International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management, VDE, 2021.
C. Charumit and V. Kinnares, “Discontinuous SVPWM techniques of three-leg VSI-fed balanced two-phase loads for reduced switching losses and current ripple,” IEEE Transactions on power electronics, vol. 30, no. 4, pp. 2191-2204, 2015. [https://doi.org/10.1109/TPEL.2014.2326773]
A. Hava, R. Kerkman, and T. A. Lipo, “A high-performance generalized discontinuous PWM algorithm,” IEEE Transactions on Industry Applications, vol. 34, no. 5, pp. 1059-1071, 1998. [https://doi.org/10.1109/28.720446]

Quantity	Symbol	Nominal value
Stator resistance	R_s	1.1 Ω
Stator inductance	L_s	0.07803 mH
Number of rotor	P	4
DC-link voltage	V_dc	24 V
Moment of intertia	J	0.004 kg - m²
Rated speed	T_R	0.062 N∙ m
Reted torque	N_R	4000 r/min
Reference speed	ω_ref	700 rpm