파라미터 보정을 가지는 풍력 동기발전기의 센서리스 최대전력 제어
Copyright © The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
초록
풍력발전용 영구자석 동기발전기의 전력제어를 위해서는 회전자의 속도 및 위치 정보가 반드시 요구된다. 그러나 위치 및 속도 센서들은 경제적인 문제점, 추가적인 센서의 부착 공간, 취약한 환경에서 신뢰도 감소 등의 단점을 가진다. 따라서 이러한 문제점들을 개선하기 위하여 회전자의 위치 검출기나 속도 센서가 없는 센서리스 제어 방식이 많이 연구되고 있다. 본 논문은 풍력발전용 동기발전기의 최대전력 제어에서 위치 및 속도센서를 제거하는 센서리스 제어에 관한 연구이다. 대부분의 센서리스 제어 방식은 전압방정식으로부터 역기전력 정보와 속도 정보를 구하게 된다. 따라서 파라미터 오차는 센서리스 제어 성능에 큰 영향을 미치게 된다. 본 논문에서는 영구자석 동기발전기의 센서리스 제어 성능을 개선하기 위해 역기전력 상수의 오차를 d축 전류의 측정치와 추정치를 이용하여 보상하는 방식을 제안하고 시뮬레이션과 실험을 통해 본 논문에서 제안한 방식을 검증한다.
Abstract
The power control of a permanent magnet synchronous generator for the wind power generation is typically implemented through measuring the rotor speed or position. However, speed and position sensors require additional mounting space, reduce their reliability in harsh environments, and increase the cost of a generator. Various control algorithms for the elimination of speed and position sensors have been proposed. This paper investigates a sensorless control that eliminates the position and speed sensors in the maximum power control of a permanent magnet synchronous generator for the wind power generation system. Most sensorless control algorithms are based on the back-EMF and speed estimations obtained from voltage equations. Therefore, the sensorless control performance is largely affected by the parameter error of a generator. A novel sensorless control with the parameter compensation is proposed for the maximum power control in this paper. The proposed parameter compensation is obtained from the d-axis current error between the real and estimated currents. The proposed algorithm is verified through simulations and experiments.
Keywords:
Wind power generation, Permanent magnet synchronous generator, Sensorless control, Pwer control, Parameter compensation키워드:
풍력발전, 영구자석 동기발전기, 센서리스 제어, 전력 제어, 파라미터 보정1. 서 론
최근 풍력발전용 발전기로서 영구자석 동기발전기가 많이 연구되고 있으며[1][2] 풍력발전용 영구자석 동기발전기의 최대전력 제어를 위해서는 회전자의 속도뿐만 아니라, 회전자의 위치 정보가 반드시 요구된다. 위치 및 속도 센서로는 엔코더, 리졸버와 같은 센서들이 사용되고 있는데, 이러한 센서들을 사용할 경우 회전자의 위치 및 속도를 직접 검출할 수 있는 장점은 있으나, 경제적인 문제점과 센서의 안정성을 확보를 위한 설계 및 가공 공정이 복잡해지는 단점이 있다. 또한, 센서는 주위환경에 영향을 받기 때문에 주위 온도가 높거나 습기가 심한 환경 또는 진동이 심한 환경에서는 센서의 신뢰도가 감소한다. 따라서 이러한 문제점들을 개선하기 위하여 회전자의 위치 검출기나 속도 센서가 없는 센서리스제어 방식이 많이 연구되고 있다. 이러한 연구로서 고정자전압 및 전류 값을 측정하여 발전기 방정식으로부터 속도를 추정하는 방식[3], 상태관측기에 의해 자속 및 역기전력을 추정하고 속도정보를 얻는 방식[4]-[6], 두 모델의 오차를 이용하여 속도를 추정하는 MRAS 방식[7], 입출력이 잡음의 영향을 받을 경우에 최적의 필터링 알고리즘인 칼만 필터를 이용하는 방식[8]-[10], 가변구조제어를 활용하는 방식[11][12], 기계적 구조에 의한 전압 및 전류 고조파를 분석하여 속도를 추정하는 방식[13], 신경 회로망 등 인공지능 활용 및 확률제어 방식[14][15], 직접토크제어를 활용하는 방식[16] 등이 있다.
대부분의 센서리스 제어 방식은 전압방정식으로부터 역기전력 정보와 속도 및 위치 정보를 구하게 된다. 따라서 파라미터 오차는 센서리스 속도 추정 성능에 큰 영향을 미치게 되며 이 파라미터 오차로 부터 발생되는 추정 오차를 보정하기 위한 여러 연구가 이루어지고 있다[1]. 본 논문은 영구자석 동기발전기의 센서리스 최대전력 제어에 관한 연구로서 본 논문에서 센서리스제어 성능을 개선하기 위해 역기전력 상수의 오차를 d축 전류의 측정치와 추정치를 이용하여 보상하는 방식을 제안하고 시뮬레이션과 실험을 통해 본 논문에서 제안한 방식을 검증한다. 본 논문에서 제안한 파라미터 보상 방식은 다른 방식에 비하여 상대적으로 간단한 장점을 가지며 시뮬레이션 및 실험을 수행한 결과 양호한 속도 추종 및 최대전력 추종 응답을 나타내고 있다.
2. 풍력발전 시스템
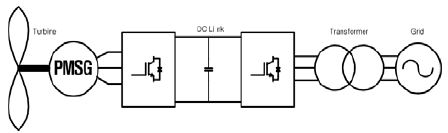
풍력발전 시스템의 일반적인 구성은 Figure 1과 같다. 풍력 발전용 영구자석 동기발전기는 풍력 터빈에 의한 회전속도에 따라서 전압과 주파수가 가변되므로 전력변환장치를 이용하여 출력을 일정 전압과 일정 주파수로 변환하여 계통에 공급한다. 풍력발전 시스템에서 풍력에너지를 최대로 활용하기 위해 영구자석 동기발전기의 최대전력 제어가 이루어지며 이를 위해서는 회전자의 위치 및 속도정보가 필요하게 된다.
풍속 vw의 풍력 에너지로부터 풍력은 터빈이라는 중간 매개체를 통해 발전기에 전달되며 터빈의 출력, 즉 발전기의 기계적인 입력은 식 (1)과 같다.
| (1) |
터빈의 출력계수는 주속비와 피치각의 함수로서 주속비는 식 (2)와 같다.
| (2) |
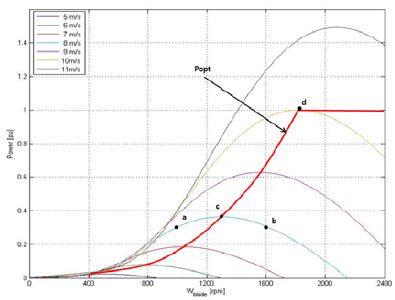
Figure 2는 풍속과 터빈 블레이드 회전속도에 따른 터빈출력, 즉 발전기 입력의 특성곡선으로서 본 논문에서 제안한 방식의 타당성을 입증하기 위하여 시뮬레이션 및 실험에 사용된 영구자석 동기발전기의 용량에 맞추어서 식 (1)로부터 계산한 결과이다. Figure 2에서 풍속과 발전기 입력의 관계는 포물선의 형태를 나타남을 알 수 있고, 이 포물선에서 기울기가 0인 지점이 최대 전력점이 된다. 만약, 풍속이 8[m/s]일 경우 터빈 블레이드 회전 속도는 400[rpm]에서 2150[rpm]까지 다양하게 운전가능하다. 그러나 운전점이 점 a인 경우와 점 b인 경우에 비해 점 c에서 터빈출력이 가장 크다는 것을 알 수 있다. 각 풍속에 따라 최대 터빈출력을 연결한 곡선이 발전기의 최대입력, 즉 최대 전력곡선이 된다.
3. 영구자석 동기발전기의 수학적 모델링
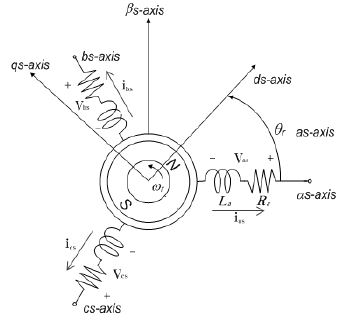
본 논문에서 사용된 영구자석 동기발전기는 원통형 영구자석 동기발전기로서 Figure 3은 영구자석 동기발전기의 등가모델을 나타낸다. Figure 3에서 Ra와 La는 각각 각 상의 등가 저항과 등가 인덕턴스를 나타내며, 각 축은 자속 기준 좌표축을 나타낸다.
3상축에서 고정자의 전압방정식을 나타내면 다음과 같다.
| (3) |
| (4) |
| (5) |
단,
식 (3) - 식 (5)의 순시 전압방정식을 좌표변환에 의하여 2상 고정자 기준 좌표계 αs-βs축의 전압방정식으로 나타내면 다음과 같이 된다.
| (6) |
| (7) |
| (8) |
| (9) |
단,
식 (3) - 식 (5)에서 전압방정식을 각속도 ωr로 회전하는 dr-qr축의 회전자 기준 좌표계로 나타내면 다음과 같이 된다.
| (10) |
| (11) |
회전자 기준 좌표계에서 영구자석 동기발전기의 입력은 다음과 같이 된다.
| (12) |
4. 파라미터 보정
식 (6) - 식 (9)로부터 영구자석 동기발전기의 상태방정식은 다음과 같이 된다.
| (13) |
| (14) |
단,
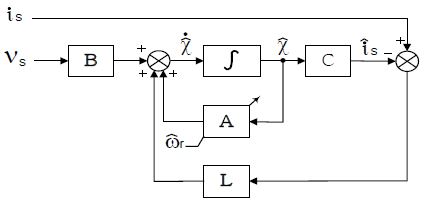
식 (13)의 상태 공간 모델을 기준으로 한 폐루프 상태관측기는 다음과 같다.
| (15) |
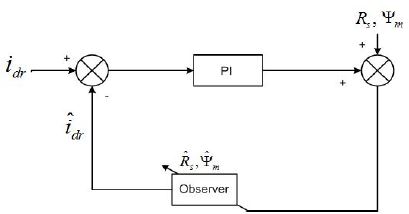
단, ^은 추정 값을 나타내고 L은 관측기 이득행렬() 이다.
Figure 4는 식 (15)를 나타낸 상태 관측기의 블록도이다.
발전기의 역기전력 항에는 발전기의 위치가 삼각함수 형태로 포함되어 있으므로 추정된 역기전력을 직접 이용하여 위치를 구하고 동기발전기의 벡터 제어를 수행할 수 있다.
| (16) |
| (17) |
전력 제어를 수행하기 위한 속도 정보도 다음과 같이 구할 수 있다.
| (18) |
| (19) |
단,
본 논문에서는 벡터 제어에서 토크 관련 q축 전류와 자속 관련 d축 전류를 각각 제어할 수 있는 점을 이용하여 파라미터 오차 성분을 d축 전류의 실제와 추정 값의 오차로 부터 보정하는 방식을 제안한다.
| (20) |
| (21) |
Figure 5는 본 논문에서 제안한 파라미터 보상 방식의 블록도이다.
5. 시뮬레이션
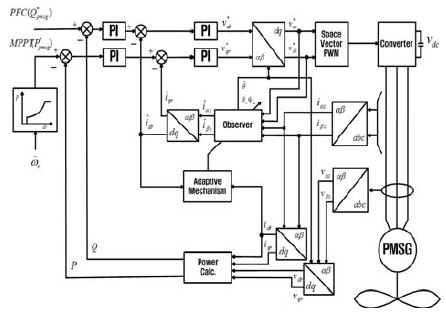
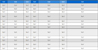
본 논문에서 제안한 파라미터 보상 방식을 가지는 영구자석 동기발전기의 센서리스 최대전력 제어 방식을 검증하기 위하여 Figure 6과 같은 전체 시스템에서 시뮬레이션을 수행하였다. 발전기 파라미터 중에서 고정자 권선의 저항과 인덕턴스는 고정자가 바깥쪽이고 자기회로가 일정하여 변동이 크지 않으며 이에 따른 운전 영향도 크지 않아 본 논문에서는 역기전력 상수 오차에 대한 파라미터 보상 시뮬레이션을 수행하였다. 시뮬레이션에서 사용된 영구자석 동기발전기의 사양은 Table 1과 같다.
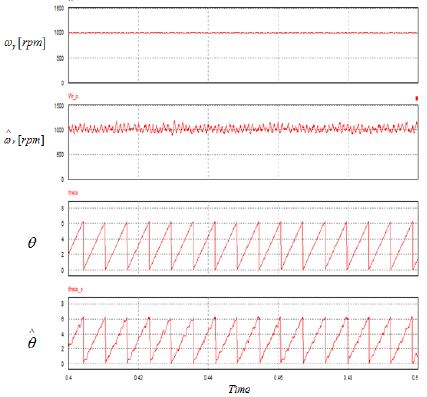
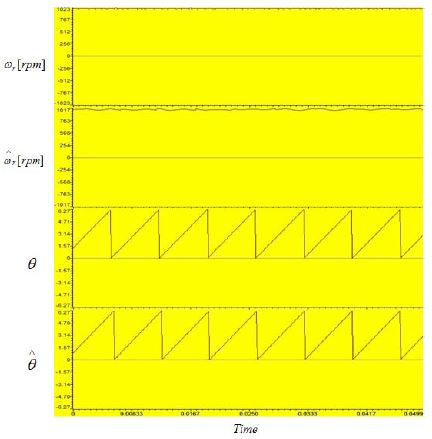
Figure 7은 동기발전기의 센서리스 최대 전력 제어에서 전차수 상태 관측기의 추정 성능을 검토하기 위해서 회전속도 1000[rpm]에서 발전기의 속도와 각도를 추정하는 시뮬레이션을 수행한 결과이다. 시뮬레이션 결과에서 추정 속도와 추정 각도가 실제 값을 양호하게 추정하고 있음을 보여주고 있다.
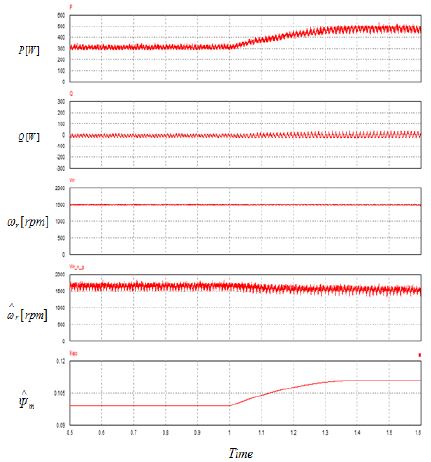
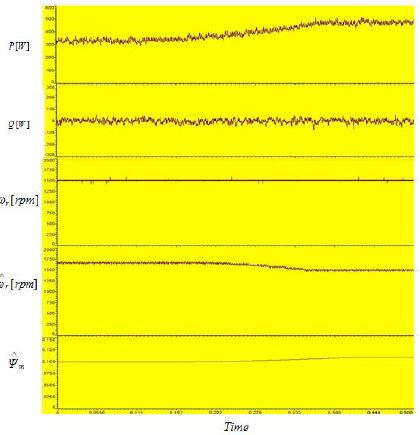
Figure 8은 회전속도 1500[rpm], 역기전력 상수 오차를 10 %로 하였을 경우 파라미터 보상 방식을 적용하지 않은 시뮬레이션 결과와 파라미터 보상 방식을 적용한 시뮬레이션 결과를 나타낸다. 시뮬레이션은 일정한 속도에서 파라미터 보상 방식을 적용하지 않고 수행한 후 특정 시간이 지난 다음 파라미터 보상 방식을 적용하여 수행하였다. Figure 8의 시뮬레이션 결과에서 제안한 보상 방식을 적용하는 경우에 최대전력제어가 양호하게 수행되고 있음을 보여주고 있다.
6. 실험결과 및 검토
본 논문에서 제안한 파라미터 보상 방식을 가지는 영구자석 동기발전기의 센서리스 최대전력 제어 방식을 검증하기 위하여 Figure 6과 같은 센서리스 최대전력 제어 시스템을 제작하여 실험을 수행하였다. 실험에 사용된 영구자석 동기발전기는 시뮬레이션에서 사용된 Table 1과 같은 발전기이고 모든 실험결과는 실험에서 샘플링 시간마다 얻어지는 데이터를 그래프로 나타낸 결과이다.
Figure 9는 동기발전기의 센서리스 최대 전력 제어에서 전차수 상태 관측기의 추정 성능을 검토하기 위해서 회전속도 1000[rpm]에서 실험을 수행한 결과이다. 실험 결과에서 추정 속도와 추정 각도가 실제 값을 양호하게 추정하고 있음을 보여주고 있다.
Figure 10은 회전속도 1500[rpm], 역기전력 상수 오차를 10 %로 하였을 경우 파라미터 보상 방식을 적용하지 않은 실험 결과와 파라미터 보상 방식을 적용한 실험 결과를 나타낸다. 실험은 일정한 속도에서 파라미터 보상 방식을 적용하지 않고 수행한 후 특정 시간이 지난 다음 파라미터 보상 방식을 적용하여 수행하였다. Figure 10에서 시뮬레이션 결과와 마찬가지로 제안한 보상 방식을 적용하는 경우에 최대전력제어가 양호하게 수행되고 있음을 보여주고 있다.
7. 결 론
대부분의 센서리스 전력 제어 방식은 전압방정식으로부터 속도 정보와 위치 정보를 구하게 된다. 따라서 파라미터 오차는 센서리스 속도 제어 성능에 큰 영향을 미치게되며 이 파라미터 오차로 부터 발생되는 추정 속도 오차를 보정하기 위한 여러 연구가 이루어지고 있다. 본 논문에서는 벡터 제어에 필요한 추정각과 추정 속도를 측정 전압과 전류로부터 구해진 역기전력을 이용하여 계산하는 전차수 상태 관측기를 사용하였으며 속도 추정에서 파라미터 오차에 의해 발생하는 속도 오차를 보상하기 위하여 파라미터를 d축 전류의 측정치와 추정치를 이용하여 보상하는 방식을 제안하였다. 제안한 알고리즘을 이용해 영구자석 동기발전기의 역기전력 상수를 실시간으로 추정하였으며 센서리스 최대 전력 제어를 검증하기 위해 센서리스 최대전력제어 시스템을 제작하고 시뮬레이션 및 실험을 수행하였다. 시뮬레이션 및 실험을 통해 파라미터 오차가 제안한 알고리즘에 의해 양호하게 보상되어 최대전력으로 제어 되는 것을 확인할 수 있었으며 본 논문에서 제안한 파라미터 보상 방식은 다른 방식에 비하여 상대적으로 간단한 장점을 가진다.
Nomenclature
| Pm : | turbine mechanical power |
| ρ : | air density |
| Rt : | turbine blade radius |
| vw : | wind speed |
| Cp : | turbine power coefficient |
| λ : | tip-speed ratio |
| β : | turbine blade pitch angle |
| ωblade : | turbine blade speed |
| vxs, ixs, Ψxs, Exs : | phase voltage, current, linkage flux, back-EMF |
| ΨM : | back-EMF coefficient |
| : | rotor angular speed |
| ηR,ηΨ : | weighted values |
| Kpr, KpΨ, Kir, KiΨ : | proportional (integral) gains |
Acknowledgments
이 논문은 부산대학교 기본연구지원사업(2년)에 의하여 연구되었음.
References
-
Y. Zhao, C. Wei, Z. Zhang, and W. Qiao, “A review on position/speed sensorless control for permanentmagnet synchronous machine-based wind energy conversion systems”, IEEE Journal of Emerging and Selected Topics in Power Electronics, vol. 1(no. 4), p203-216, (2013).
[https://doi.org/10.1109/jestpe.2013.2280572]

-
D. M. Miao, and J. X. Shen, “Comparative study on permanent magnet synchronous generator systems with various power conversion topologies”, Proceedings of POWERENG, p1738-1743, (2013).
[https://doi.org/10.1109/powereng.2013.6635880]

-
M. Pacas, “Sensorless drives in industrial applications”, IEEE Industrial Electronics Magazine, vol. 5(no. 2), p16-23, (2011).
[https://doi.org/10.1109/mie.2011.941125]

- L. Tong, X. Zou, S. Feng, Y. Chen, Y. Kang, Q. Huang, and Y. Huang, “An SRF-PLL-based sensorless vector control using the predictive deadbeat algorithm for the direct-driven permanent magnet synchronous generator”, IEEE Transactions on Power Electronics, vol. 29(no. 6), p2837-2849, (2014).
-
A. Urtasun, P. Sanchis, and L. Marroyo, “Small wind turbine sensorless MPPT: Robustness analysis and lossless approach”, IEEE Transactions on Industry Applications, vol. 50(no. 6), p4113-4121, (2014).
[https://doi.org/10.1109/tia.2014.2313650]

-
K. W. Hu, and C. M. Liaw, “Position sensorless surface- mounted permanent-magnet synchronous generator and its application to power DC microgrid”, IET Power Electronics, vol. 8(no. 9), p1636-1650, (2015).
[https://doi.org/10.1049/iet-pel.2014.0197]

-
H. C. Tseng, and S. Cheng, “Robust sensorless control of PMSG with MRAS in variable speed wind energy conversion system”, Proceedings of ICMA, p1917-1922, (2011).
[https://doi.org/10.1109/icma.2011.5986273]

-
B. Aubert, J. Regnier, S. Caux, and D. Alejo, “Stator inter-turn short-circuit detection in permanent magnet synchronous generators using extended Kalman filtering”, Proceedings of ECMSM, p1-6, (2013).
[https://doi.org/10.1109/ecmsm.2013.6648943]

-
M. Benadja, and A. Chandra, “Adaptive sensorless control of PMSGs-based offshore wind farm and VSC-HVdc stations”, IEEE Journal of Emerging and Selected Topics in Power Electronics, vol. 3(no. 4), p918-931, (2015).
[https://doi.org/10.1109/jestpe.2015.2453113]

-
G. Rigatos, P. Siano, and N. Zervos, “Sensorless control of distributed power generators with the derivative- free nonlinear Kalman filter”, IEEE Transactions on Industrial Electronics, vol. 61(no. 11), p6369-6382, (2014).
[https://doi.org/10.1109/tie.2014.2300069]

-
F. Xiao, H. X. Wang, M. L. Chen, and Y. Liu, “A novel sensorless control of PMSG based on sliding mode obsever”, Proceedings of ICEM, p1-4, (2010).
[https://doi.org/10.1109/icelmach.2010.5608175]

-
E. Elmahersi, A. Khedher, and M. F. Mimouni, “An adaptive sliding mode flux observer applied to wind-PMSG system controlled by VC and SMC”, Proceedings of EVER, p1-7, (2013).
[https://doi.org/10.1109/ever.2013.6521531]

-
D. D. Reigosa, F. Briz, C. Blanco, and J. M. Guerrero, “Sensorless control of doubly fed induction generators based on stator high-frequency signal injection”, IEEE Transactions on Industry Applications, vol. 50(no. 5), p3382-3391, (2014).
[https://doi.org/10.1109/tia.2014.2303255]

-
M. Singh, and A. Chandra, “Application of adaptive network-based fuzzy inference system for sensorless control of PMSG-based wind turbine with nonlinear-load-compensation capabilities”, IEEE Transactions on Power Electronics, vol. 26(no. 1), p165-175, (2011).
[https://doi.org/10.1109/tpel.2010.2054113]

-
T. S. Zhan, J. L. Chen, S. J. Chen, C. H. Huang, and C. H. Lin, “Design of a chaos synchronization based maximum power tracking controller for a wind-energy-conversion system”, IET Renewable Power Generation, vol. 8(no. 6), p590-597, (2014).
[https://doi.org/10.1049/iet-rpg.2013.0268]

-
Z. Zhang, Y. Zhao, W. Qiao, and L. Qu, “A space-vector-modulated sensorless direct-torque control for direct-drive PMSG wind turbines”, IEEE Transactions on Industry Applications, vol. 50(no. 4), p2331-2341, (2014).
[https://doi.org/10.1109/tia.2013.2296618]