Performance analysis of an organic Rankine cycle for a solar-boosted ocean thermal energy conversion system according to working fluids
Copyright ⓒ The Korean Society of Marine Engineering
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
Ocean Thermal Energy Conversion is a power generation cycle that utilizes temperature differences between warm surface seawater and cool deep seawater. A study on Solar-boosted Ocean Thermal Energy Conversion (SOTEC) that utilizes not only ocean thermal energy, but also solar thermal energy as a heat source has been recently researched. In SOTEC, the temperature of surface seawater is boosted using a solar thermal collector. The working fluids and cycle configuration are important factors that affect the thermal performance of an organic Rankine cycle in SOTEC. The simple Rankine cycle and the Rankine cycle with an open feedliquid heater were considered in this study. Working fluids were selected depending upon working conditions, environment, and safety factors. Exergy analysis is an important criterion for the thermal performance evaluation of cycles. This study performed exergy analysis on cycles based on SOTEC. This analysis showed that RE245fa2 has the best thermodynamic performance among the working fluids tested. The exergy efficiency of RE245fa2 was 64.76% in the simple Rankine cycle and 67.79% in the Rankine cycle with an open feedliquid heater. In the Rankine cycle with an open feedliquid heater, an increase in thermodynamic performance could be expected in a SOTEC system, compared to the simple Rankine cycle.
Keywords:
Solar-boosted ocean thermal energy conversion, Working fluid, Organic Rankine cycle, Exergy analysis1. Introduction
Research shows that the environmental issues of pollution, global warming, and energy shortage are gradually increasing [1]. A new regeneration energy method is one way to solve these problems.
Ocean Thermal Energy Conversion (OTEC) is a power generation cycle that utilizes temperature differences between warm surface seawater and cool deep seawater [2]. OTEC can obtain sufficient economic feasibility in cases where the temperature difference between surface seawater and deep seawater is greater than 20°C [3]. The potential energy reserves of the ocean temperature difference are approximately 4000 times that of the annual global energy consumption [4]. Therefore, due to the benefits of sustainable clean energy, many countries such as USA and Japan have conducted continued research on OTEC [5].
A study on Solar-boosted Ocean Thermal Energy Conversion (SOTEC) that uses not only ocean thermal energy, but also solar thermal energy as a heat source has been recently researched. In a SOTEC system, the temperature of surface seawater is boosted using a solar thermal collector. Yamada et al. showed that the thermal efficiency of a proposed SOTEC plant was approximately 1.5 times higher than that of conventional OTEC plants [6].
The use of an Organic Rankine Cycle (ORC) is necessary because the temperature difference between the heat source and the heat sink is too low in OTEC systems [7]. Therefore, research into the ORC characteristics required to implement this technology is needed. Cycle configuration and working fluids will affect the cycle performance greatly. Kim et al. investigated an ORC for OTEC systems, and conducted a performance analysis of the working fluids and cycles [8].
The objectives of this study are to investigate the efficiency of various cycles, select an appropriate working fluid, define the design factors, and perform an exergy analysis on a SOTEC system.
2. Organic Rankine cycle for SOTEC
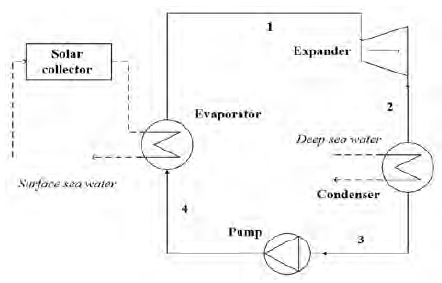
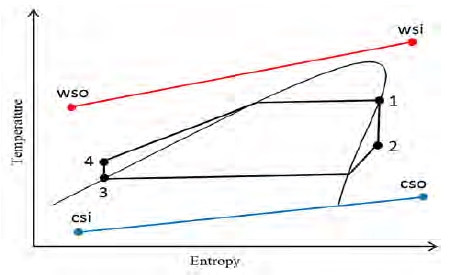
Figure 1 and Figure 2 show the schematic diagram and the T-s diagram of the simple Rankine cycle for SOTEC, respectively. The simple Rankine cycle is a basic cycle in the OTEC system [8]. In a SOTEC system, the surface seawater receives additional heat energy from a solar collector. It is expected that there will be an increase in the turbine inlet temperature and thermal efficiency. This study referred to the research of Yamada et al. [6], which defined an “indirect” SOTEC system. The basic principles and thermodynamic equations of the simple Rankine cycle are detailed in the study by Kim et al. [8][9].
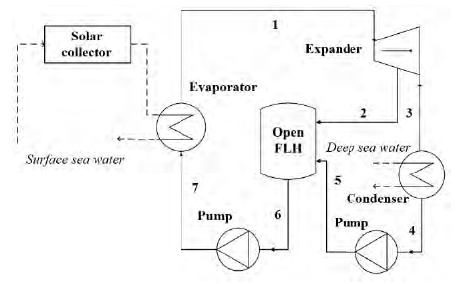
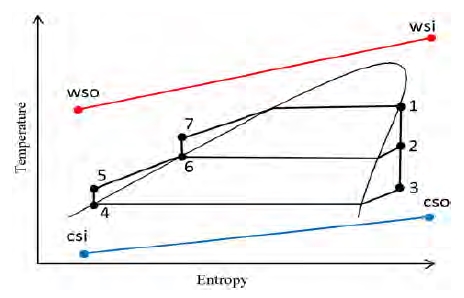
Figure 3 and Figure 4 show the schematic diagram and the T-s diagram of the Rankine cycle with an open feedliquid heater for SOTEC, respectively. It has a regenerator called “an open feedliquid heater,” that mixes the liquid discharged by a working fluid pump and bleeds gas from the turbine outlet [10]. This cycle is expected to have an increase in efficiency when compared to the simple Rankine cycle [11]-[13]. Thermodynamic states of this cycle can be expressed in Equations (1) - (13), according to the first and second laws of thermodynamics, based on energy and exergy analysis.
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
In the Rankine cycle with open feedliquid heaterankine cycle with an open feedliquid heater, the pressure ratio (fp) needs to be defined because of the existence of a medium pressure (Pmid) exists [8][12][13]. After the high pressure (Phigh) and low pressure ( Plow) are determined, the medium pressure (Pmid) can be defined as follows.
| (14) |
3. Cycle analysis condition
3.1 Selection of working fluids
A study by Kim et al. [8][9] was referred to in the selection of working fluids for this study. Working fluids were selected by referring to NIST Refprope. CFC and HCFC affiliated refrigerants that have caused environmental problems, such as ozone depletion and global warming, were excluded due to environmental regulations. Working fluids demanding that evaporation is above 3 MPa or critical pressure in design condition were additionally excluded. All the working fluids selected have an Atmosphere Life Time (ALT) less than 1,000 years, a Global Warming Potential (GWP) less than 1,500, and an Ozone Depletion Potential (ODP) of 0. The American Society of Heating, Refrigerating and Air-conditioning Engineers (ASHRAE) safety group of the fluids was also considered, and fluids in groups Al, A2L, and A2 were chosen as they have low toxicity and flammability. Seven working fluids, shown in Table 1, were selected. They can be classified into dry, isentropic, and wet fluid categories.
3.2 Design parameters of the cycle
Pinch Point Analysis (PPA) is a thermodynamic cycle analysis method that uses Pinch Point Temperature Difference (PPTD) [14]. The PPTD ensures that the temperature and pressure in an evaporator and a condenser are constantly maintained, so that a comparison analysis of each cycle and the various working fluids can be performed. The design parameters of this study, shown in Table 2, were based on previous research that used PPA [8][9]. The PPTD of the heat exchangers is the same value as was used in the research of Aydin et al. [15]. The temperature increase in the surface seawater due to the solar collector was assumed to be 20°C, as chosen by Yamada et al. [6]. Aspen HYSYS, a thermal process and cycle design program, was used as an analysis tool. A SOTEC system was replicated using this program. The selected working fluids were applied, and the thermodynamic performance was calculated in each cycle.
3.3 Peng-Robinson equation
Since the ideal gas equation has limited use in practical applications, the real gas state equations were used to precisely indicate the state of the substance [10]. In this study, the Peng-Robinson equation was used as well as the real gas state equations, and they can be expressed as follows.
| (15) |
| (16) |
| (17) |
| (18) |
| (19) |
| (20) |
4. Results and discussion
4.1 Simple Rankine cycle
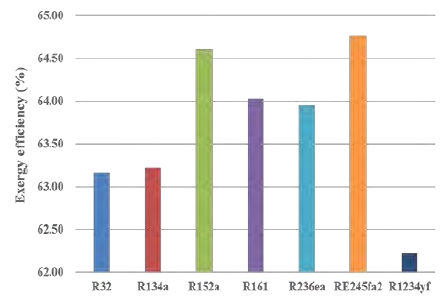
Figure 5 shows the exergy efficiency of the simple Rankine cycle in a SOTEC system, referring to the study by Kim et al. [8][9]. RE245fa2 showed the highest exergy efficiency (64.76%) and R1234yf showed the lowest exergy efficiency (62.23%). These results are similar to those of the study by Kim et al. [8][9] that performed thermodynamic comparison analysis of various working fluids in an OTEC system. Therefore, RE245fa2 showed the best thermodynamic performance among the selected working fluids, and has the potential to be a working fluid in a SOTEC system as well as an OTEC system.
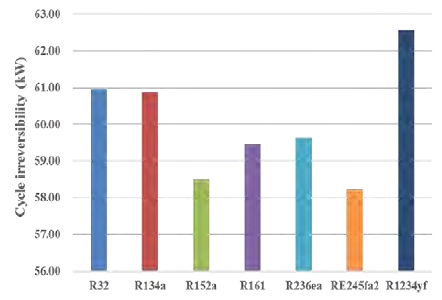
Figure 6 shows cycle irreversibility of the simple Rankine cycle in a SOTEC system, by referring to the study by Kim et al. [8][9]. R1234yf showed the highest cycle irreversibility (62.57 kW), and RE245fa2 showed the lowest cycle irreversibility (58.24 kW). Cycle irreversibility is the difference between reversible work and useful work [10]. The cycle irreversibility of the working fluids was inversely proportional to exergy efficiency. The reason for this phenomenon is that the recovered exergy decreases as the exergy is destroyed, which means cycle irreversibility increases [10]. Exergy destruction is greatly influenced by the entropy generation of a cycle and the ambient temperature.
4.2 Rankine cycle with an open feedliquid heater
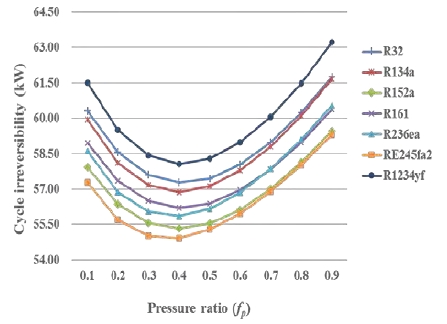
Figure 7 shows exergy efficiency of the Rankine cycle with an open feedliquid heater vs. the pressure ratio in a SOTEC system. This was calculated using Equation (13). All of the selected working fluids showed peak thermal performance during this cycle when the pressure ratio was 0.4. This means that the quantity of vapor bled from the turbine should provide this pressure ratio for maximum efficiency.
Figure 8 shows exergy efficiency of the Rankine cycle with an open feedliquid heater, when the pressure ratio is 0.4, compared to the simple Rankine cycle in a SOTEC system. RE245fa2 showed the highest exergy efficiency (67.79%). R1234yf, which had the lowest exergy efficiency, had the greatest increase in exergy efficiency (3.78%), and R152a showed the smallest increase of 2.96%. The selected working fluids showed different thermodynamic characteristics, such as mass flow and enthalpy, depending on the design conditions.
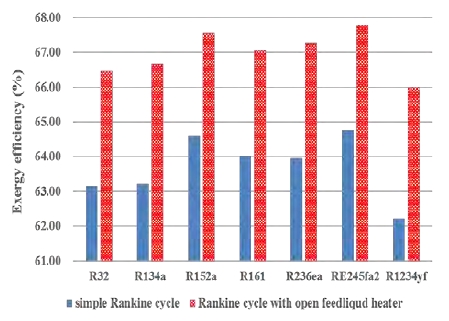
Exergy efficiency of the Rankine cycle with an open feedliquid heater compared to the simple Rankine cycle
Figure 9 shows cycle irreversibility of the Rankine cycle with an open feedliquid heater vs. the pressure ratio in a SOTEC system. This was calculated using Equation (11). All of the selected working fluids showed the lowest cycle irreversibility during this cycle when the pressure ratio was 0.4. This is because the cycle irreversibility of working fluids is inversely proportional to exergy efficiency, as mentioned previously.
Figure 10 shows the cycle irreversibility of the Rankine cycle with an open feedliquid heater when the pressure ratio is 0.4, compared to the simple Rankine cycle. R1234yf showed the highest cycle irreversibility (58.07 kW) and the greatest decrease in cycle irreversibility (4.50 kW). R152a showed the lowest decrease (3.17 kW). The cycle irreversibility of all the working fluids is affected by the entropy generation in this cycle.
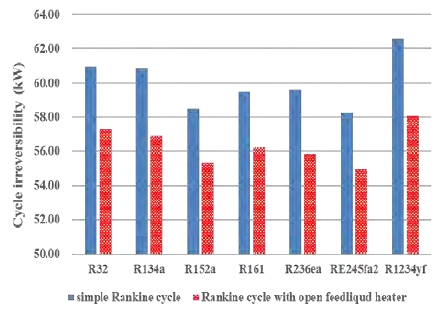
Cycle irreversibility of the Rankine cycle with an open feedliquid heater compared to the simple Rankine cycle
All of the selected working fluids in this cycle showed an improvement in thermodynamic performance, as seen in the results of the studies by Kim et al. [8][9], Shin et al. [12], and Kim et al. [13]. Therefore, to further improve thermodynamic performance, the installation of multiple regenerators (open or closed type of feedliquid heaters) has been proposed [10].
5. Conclusion
In the organic Rankine cycle for a SOTEC system, RE245fa2 showed the best thermodynamic performance in this study. The exergy efficiency of RE245fa2 was 64.76% in the simple Rankine cycle and 67.79% in the Rankine cycle with an open feedliquid heater. However, there was no significant performance difference when different working fluids were used. Therefore, when selecting a working fluid not only the thermodynamic performance but also the environmental and safety factors, which are of the utmost importance, should be considered.
In the case of the Rankine cycle with an open feedliquid heater, the ideal pressure ratio with regard to the medium pressure was 0.4. The Rankine cycle with an open feedliquid heater showed cycle performance improvements when compared to the simple Rankine cycle. It can be expected that better cycle performance improvements can be achieved using additional feedliquid heaters or other regenerative design methods. Finally, future work should consider the economic feasibility of SOTEC when the hardware of an organic Rankine cycle is added.
Nomenclature
| fp : | Pressure ratio |
| h : | Enthalphy |
| : | Irreversibility rate |
| : | Mass flow rate |
| P : | Pressure |
| Phigh : | High pressure |
| Pliq : | Liquid pressure |
| Plow : | Low pressure |
| Pmid : | Medium pressure |
| Pvap : | Vapour pressure |
| : | Heat rate |
| R : | Gas constant |
| s : | Entropy |
| T : | Pressure |
| T0 : | Ambient temperature |
| TH : | Heat source temperature |
| TL : | Heat sink temperature |
| TR : | Reduced temperature |
| Vm : | Molar volume |
| : | Power |
| η : | Efficiency |
| ω : | Acentric factor |
Subscript
| a : | Vapour except bleeding |
| b : | Bleeding vapour |
| c : | Condenser |
| crit : | Critical |
| csi : | Cooling seawater inlet |
| cso : | Cooling seawater outlet |
| e : | Evaporator |
| p : | Pump |
| r : | Feedliquid heater |
| t : | Turbine |
| th : | Thermal |
| total : | Total |
| wsi : | Warm seawater inlet |
| wso : | Warm seawater outlet |
| 𝛱 : | Second law, Exergy |
Acknowledgments
This paper is extended and updated from the short version that appeared in the Proceedings of the International symposium on Marine Engineering and Technology (ISMT 2016), held at Korea Maritime and Ocean University, Busan, Korea on November 3-4, 2016.
This work was supported by the Korea Institute of Energy Technology Evaluation and Planning (KETEP) and the Ministry of Trade, Industry & Energy (MOTIE) of the Republic of Korea (No. 20133030000110)
References
-
F. Sun, Y. Ikegami, B. Jia, and H. Arima, “Optimization design and exergy analysis of organic Rankine cycle in ocean thermal energy conversion”, Journal of the Applied Ocean Research, 35, p38-46, (2012).
[https://doi.org/10.1016/j.apor.2011.12.006]

-
R. Soto, and J. Vergara, “Thermal power plant efficiency enhancement with ocean thermal energy conversion”, Journal of the Applied Thermal Engineering, 62(1), p105-112, (2014).
[https://doi.org/10.1016/j.applthermaleng.2013.09.025]

-
M. H. Yang, and R. H. Yeh, “Analysis of optimization in an OTEC plant using organic Rankine cycle”, Journal of the Renewable Energy, 68, p25-34, (2014).
[https://doi.org/10.1016/j.renene.2014.01.029]

- L. A. Vega, “Ocean thermal energy conversion primer”, Journal of the Marine Technology Society, 6(4), p25-35, (2003).
- H. J. Kim, H. S. Lee, Y. K. Jung, D. H. Jung, D. S. Moon, and S. W. Hong, “Feasibility study on the commercial plant of ocean thermal energy conversion (OTEC-K50)”, Proceedings of the Twenty-second International Offshore and Polar Engineering Conference, p763-768, (2012).
-
N. Yamada, A. Hoshi, and Y. Ikegami, “Performance simulation of solar-boosted ocean thermal energy conversion plant”, Journal of the Renewable Energy, 34(7), p1752-1758, (2009).
[https://doi.org/10.1016/j.renene.2008.12.028]

-
B. F. Tchanche, G. Lambrinos, A. Frangoudakis, and G. Papadakis, “Low-grade heat conversion into power using organic Rankine cycles - A review of various applications”, Journal of the Renewable and Sustainable Energy Reviews, 15(8), p3963-3979, (2011).
[https://doi.org/10.1016/j.rser.2011.07.024]

-
J. S. Kim, D. Y. Kim, Y. T. Kim, and H. K. Kang, “Performance analysis of an organic Rankine cycle for ocean thermal energy conversion system according to the working fluid and the cycle”, Journal of the Korean Society of Marine Engineering, 39(9), p881-889, (2015), (in Korean).
[https://doi.org/10.5916/jkosme.2015.39.9.881]

-
J. S. Kim, D. Y. Kim, H. K. Kang, and Y. T. Kim, “Performance analysis of an organic Rankine cycle for ocean thermal energy conversion system according to pinch point temperature difference”, Journal of the Korean Society of Marine Engineering, 40(6), p476-483, (2016), (in Korean).
[https://doi.org/10.5916/jkosme.2016.40.6.476]

- Y. A. Cengel, and M. A. Boles, Thermodynamics, Seoul, South Korea, McGraw-Hill Education Korea, (2011).
- B. F. Tchanche, M. Petrissans, and G. Papadakis, “Heat resources and organic Rankine cycle machines”, Journal of the Renewable and Sustainable Energy Reviews, 39, p1185-1199, (2014).
- S. H. Shin, D. S. Jung, C. B. Kim, and T. B. Seo, “A study of ocean thermal energy conversion systems using Kalina cycle and regenerative Rankine cycle”, Journal of the Korean Solar Energy Society, 19(3), p101-113, (1999), (in Korean).
- N. J. Kim, S. H. Shin, and W. G. Chun, “A study on the thermodynamic cycle of OTEC system”, Journal of the Korean Solar Energy Society, 26(2), p9-18, (2006), (in Korean).
-
D. Wang, X. Ling, and H. Peng, “Performance analysis of double organic Rankine cycle for discontinuous low temperature waste heat recovery”, Journal of the Applied Thermal Engineering, 48, p63-71, (2012).
[https://doi.org/10.1016/j.applthermaleng.2012.04.017]

-
H. Aydin, H. S. Lee, H. J. Kim, S. K. Shin, and K. Park, “Off-design performance analysis of a closed-cycle ocean thermal energy conversion system with solar thermal preheating and superheating”, Journal of the Renewable Energy, 72, p154-163, (2014).
[https://doi.org/10.1016/j.renene.2014.07.001]